Олимпиада по математике Школьный тур

Олимпиада по математике

Школьный тур

8 класс

1. Решите уравнение x - 6 = |x - 3|/(x - 3).
2. Верно ли равенство 3¹⁰⁰ + 7¹⁰⁰ = 8¹⁰⁰? Ответ обоснуйте.
3. Дворники получают грабли и метлы. Если каждый возьмет одну метлу или одни грабли, то останется 14 метел. А чтобы дать каждому дворнику и одну метлу, и одни грабли, не хватает 10 грабель. Сколько было дворников, сколько метел и сколько грабель?
4. На острове живут два племени: аборигены и пришельцы. Аборигены всегда говорят правду, а пришельцы всегда лгут. Путешественник, приехавший на остров, нанял островитянина в проводники. Они пошли и увидели другого островитянина. Путешественник послал туземца узнать, к какому племени принадлежит этот туземец. Проводник вернулся и сказал: «Туземец говорит, что он абориген». Кем был проводник: пришельцем или аборигеном? Ответ обоснуйте.
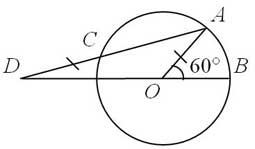
5. В окружности с центром в точке О проведены радиусы ОВ и ОА так, что ﮮАОВ=60°, ОВ = DС. Найдите величину ﮮАDО.

                                                    11 класс

1. Решите уравнение .
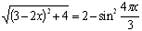2. Функция y = f(x) определена на множестве всех действительных чисел и является периодической с периодом 5. Найдите значение выражения 
     f(-6) + f(19) – f(-13), если f(-1) = -2 и f(2) = 3,5.
3. Какую наибольшую длину может иметь ребро правильного тетраэдра, который помещается в коробку, имеющую форму куба со стороной 1 см? Ответ обоснуйте.
4. Докажите, что x⁴ + y⁴ + z² + 1 >= 2x (xy² – x + z + 1).
5. Сторона основания правильной треугольной пирамиды равняется а, а боковое ребро равняется b. Плоскость, параллельная боковому ребру и проходящая через скрещивающуюся с ним сторону основания, пересекает пирамиду по квадрату. Вычислите сторону квадрата.

6 класс

1. Если Коля купит 11 тетрадей, то у него останется 7 рублей, а на покупку 15 тетрадей ему не хватит 5 рублей. Сколько денег у Николая? Ответ обоснуйте.
2. Какова последняя цифра ответа 2003 · 2005 · 2007 – 2000 · 2008? Ответ обоснуйте.
3. Как разложить семь алмазов в четыре одинаковые шкатулки, чтобы вес всех шкатулок получился одинаковым, если вес алмазов 1, 2, 3, 4, 5, 6, 7. граммов. Ответ обоснуйте.
4. На одной чаше весов лежит кусок мыла, на другой 2/3   такого же куска и еще 2/3 кг. Сколько весит весь кусок мыла? Ответ обоснуйте.
5. Четыре ученика – Витя, Петя, Юра и Сергей – заняли на математической Олимпиаде  четыре первых места. На вопрос, какие места они заняли, были даны ответы:

а)   Петя – второе, Витя – третье;

б)   Сергей – второе, Петя – первое;

в)   Юра – второе, Витя – четвертое.

Укажите, кто какое место занял, если в каждом ответе правильна лишь одна часть. Ответ обоснуйте.

5 класс

1.   Вычеркните в числе 4000538 пять цифр так, чтобы остав­шееся число стало наибольшим.

2.   Для того чтобы разрезать металлическую балку на две части, нужно уплатить за работу 5 рублей. Сколько будет стоить работа, если балку нужно разрезать на 10 частей?

3.   Парусник отправляется в плавание в понедельник в пол­день. Плавание будет продолжаться 100 часов. Назовите день и час его возвращения в порт.

4.   Разбейте циферблат часов (см. рис. 1) с помощью отрезков на три части таким образом, чтобы сумма чисел в каждой из этих частей была одной и той же.

5.   На улице, став в кружок, беседуют четыре девочки: Аня, Валя, Галя, Надя. Девочка в зеленом платье (не Аня и не Ва­ля) стоит между девочкой в голубом платье и Надей. Девочка в белом платье слоит между девочкой в розовом платье и Валей. Какое платье носит каждая из девочек?

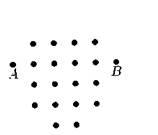
6.   Соедините точки А и В (см. рис. 2) линией длиной 19 см так, чтобы она прошла через все точки, изображенные на рисунке (расстояние между двумя соседними точками, расположенными горизонтально или вертикально, равно 1 см).

7 класс

1. Не выполняя деления, выясните, делится ли значение выражения 37 · 124 + 21 · 124 + 58 · 554 на 678. Ответ обоснуйте.
2. Средний возраст 11 игроков футбольной команды 22 года. Когда одного игрока удалили с поля, средний возраст оставшихся игроков составил 21 год. Сколько лет удаленному игроку? Ответ обоснуйте.
3. Какова сумма всех цифр, используемых для записи всех натуральных чисел от 1 до  1 000 000? Ответ обоснуйте.
4. 2% натурального числа А больше, чем 3% натурального числа В. Верно ли, что  5%  числа  А  больше, чем  7%  числа В?  Ответ обоснуйте.
5. Ваня, Петя, Саша и Коля носят фамилии, начинающиеся на буквы В, П, С и К.  Известно, что 

a.Ваня и С. – отличники;

b.Петя и В. – троечники;

c.В. ростом выше П.;

d.Коля ростом ниже П.;

e.Саша и Петя имеют одинаковый рост.

На какую букву начинается фамилия каждого мальчика? Ответ обоснуйте.

9 класс

1.      На доске написаны восемь простых чисел, каждое из которых больше двух. Может ли их сумма равняться 59?

2.      Для каких  значений  а  разность корней уравнения  х²+ах+10=0  равна 3?

3.        В треугольнике АВС медиана ВМ в два раза меньше стороны АВ и образует с ней угол 40^o . Найдите угол АВС .

4.      Освободитесь от иррациональности в знаменателе дроби: .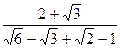

5. У подводного царя служат осьминоги с шестью, семью или восемью ногами. Те, у кого 7 ног, всегда лгут, а у кого 6 или 8 ног, всегда говорят правду. Встретились четыре осьминога. Синий сказал: "Вместе у нас 28 ног", зеленый: "Вместе у нас 27 ног", желтый: "Вместе у нас 26 ног", красный: "Вместе у нас 25 ног". У кого сколько ног?