Олимпиадные задания по учебной дисциплине "Математика" для студентов СПО

Бюджетное профессиональное образовательное учреждение

Вологодской области

«Тотемский политехнический колледж»

Материалы к внутриколледжной олимпиаде

по учебной дисциплине  ОУД.04 «Математика»

2019- 2020 учебный год, 1курс

Преподаватель: Пинигина О. В.

Тотьма

2019

Пояснительная записка.

Цель: выявление и поддержка способных студентов, студентов с высоким уровнем познавательной активности.

Задачи:

-         повысить интерес студентов к учебной дисциплине «Математика»;

-         повысить уровень подготовки студентов по математике;

-         развивать навыки творческого применения полученных знаний;

-         привлечь к более глубокому изучению математики более широкие круги студентов.

Олимпиадные задания составлены по следующим разделам: «Задачи с геометрическим содержанием», «Числовые задачи», «Решение  уравнений», «Задачи на работу».

Время выполнения: 2 часа.

Критерии и нормы оценки:

Олимпиада состоит из семи заданий. Студенты должны представить подробное решение каждого задания. Каждое задание оценивается по 7 баллов. Максимальное количество баллов – 49.

Установлены следующие критерии оценки олимпиадных работ:

 1 и 2 места определяются при выполнении студентом не менее 50% работы.

Олимпиада по математике, 2019- 2020 учебный год, 1 курс

1.   Петя в сутки тратит 1/3 своего времени на игру в футбол, 1/5 — на учебу в школе, 1/6 — на просмотр кинофильмов, 1/7 — на решение олимпиадных задач, и 1/3 — на сон. Можно ли так жить? Ответ поясните.

2.   Запишите число 10 с помощью семи «4», знаков арифметических действий и запятых.

3.   Три подруги были в белом, красном и голубом платьях. Их туфли были так же трех цветов. Только у Тамары цвета платья и туфель совпадали. Валя была в белых туфлях. Ни платье, ни туфли Лиды не были красными. Определите цвет платья и туфель каждой из подруг.

4.   Сколько цифр содержит число 4⁵ · 5¹³?

5.  Решите уравнение  х² + 2х +  = 30

6.   В прямоугольнике ABCD сторона AB равна 6, сторона BC равна 11. Из вершин B и C проведены биссектрисы углов, пересекающие сторону AD в точках X и Y соответственно. Найдите длину отрезка XY .

7.   Двое рабочих могут выполнить некоторую работу за 7 дней при условии, что второй приступит к ней на 2 дня позже первого. Если бы ту же работу каждый выполнял в одиночку, то первому потребовалось бы на 4 дня больше, чем второму. За сколько дней каждый рабочий мог бы выполнить эту работу?

Время выполнения – 2 часа. Каждая задача оценивается по 7 баллов. Желаем успеха!

Решения заданий олимпиады.

2019 - 2020 год.

( каждое задание оценивается   в 7 баллов)

Основные принципы оценивания приведены в таблице.

1.                  Петя в сутки  тратит 1/3 своего времени на игру в футбол, 1/5 — на учебу в школе, 1/6 — на просмотр кинофильмов, 1/7 — на решение олимпиадных задач, и 1/3 — на сон. Можно ли так жить?

Решение:

Поскольку 1/5 + 1/6 > 1/3, то сумма данных дробей 1/3 + 1/5 + 1/6 + 1/7 + 1/3 > 1, что противоречит здравому смыслу. Нет, так жить нельзя.

2.                 Запишите число 10 с помощью семи «4», знаков арифметических

 действий и запятой.

Решение:

Например : 44,4:4 – 4,4:4 = 10

3.                 Три подруги были в белом, красном и голубом платьях. Их туфли были так же трех цветов. Только у Тамары цвета платья и туфель совпадали. Валя была в белых туфлях. Ни платье, ни туфли Лиды не были красными. Определите цвет платья и туфель каждой из подруг.

Решение:

          Ответ: у Тамары были красные туфли и платье, у Вали – белые туфли и

          голубое платье, у Лиды – белое платье и голубые туфли.

4.                 Сколько цифр содержит число 4⁵ · 5¹³?

Решение:

4⁵ · 5¹³ = (2¹⁰ · 5¹⁰)· 5³ = 10¹⁰ · 5³ = 1250000000000

Ответ: 13 цифр.

5.         Решите уравнение  х² + 2х +  = 30

Решение:

Обозначим   = t,  где t ≥ 0 . Тогда получим: t² + 2t – 15 = 0. Откуда t₁ = - 5 – посторонний корень, t₂ = 3. Значит,  = 3,  = 9,  = 0. Откуда х₁ = - 6; х₂ = 4.

Ответ: - 6; 4.

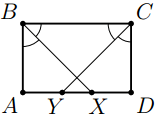
6.                 В прямоугольнике ABCD сторона AB равна 6, сторона BC равна 11. Из вершин B и C проведены биссектрисы углов, пересекающие сторону AD в точках X и Y соответственно. Найдите длину отрезка XY .

Ответ: 1.

Решение. Углы AXB и XBC равны как накрест лежащие при параллельных прямых AD и BC и секущей BX. Углы XBC и XBA равны, так как BX — биссектриса угла ABC. Получаем, что ∠AXB = ∠XBA, откуда следует, что треугольник AXB — равнобедренный, AB = AX = 6;

XD = AD — AX = 11 — 6 = 5. Аналогично получаем, что AY = 5. Тогда XY = AD — AY — XD = 11 —5 — 5 = 1.

Критерии. Любое верное решение: 7 баллов.

Доказано, что AY = 5, но при этом длина отрезка XY не найдена или найдена неверно: 4 балла.

Доказано, что треугольник ABX равнобедренный и нет дальнейших продвижений: 2 балла.

Приведён только верный ответ: 0 баллов

7.                 Двое рабочих могут выполнить некоторую работу за 7 дней при условии, что второй приступит к ней на 2 дня позже первого. Если бы ту же работу каждый выполнял в одиночку, то первому потребовалось бы на 4 дня больше, чем второму. За сколько дней каждый рабочий мог бы выполнить эту работу?

Решение:

Обозначим за  х  дней – время, за которое второй рабочий смог бы выполнить всю работу  один, получим уравнение  7·   + 5 ·  = 1. Решая его , найдём время работы  второго рабочего: 10 дней. Тогда время работы первого рабочего будет 14 дней.

Ответ: 14 и 10 дней.