Онспект укока по теме "Область определения и множество значений тригонометрических функций"

Урок                                                                                                                                         А 11

Область определения и множество значений тригонометрических функций

Цели урока:

Образовательные: введение понятия тригонометрических функций; формировать умения исследовать область определения и множество значений тригонометрических функций.

Воспитательные: воспитание познавательного интереса к учебному процессу; формирование умения анализировать поставленную задачу; воспитание эмоционально-положительной направленности на практическую деятельность; воспитание информационной культуры учащихся;

Развивающие: формирование навыков проводить анализ ситуации с последующим выбором наиболее рационального выхода из нее; развитие познавательного интереса учащихся; развитие математически грамотной речи, логического мышления, сознательного восприятия учебного материала

Оборудование: учебник

Ход урока

1.     Организационный момент

2.     Постановка темы, цели и задач урока

3.     Актуализация опорных знаний учащихся

Ответить на вопросы:

1.      Что такое функция? (Если каждому значению x из некоторого множества чисел поставлено в соответствие по определенному правилу число y, то говорят, что на этом множестве задана функция. При этом х называют независимой переменной или аргументом, а у – зависимой переменной или функцией. Зависимость переменной у от переменной х называют функциональной зависимостью. Записывают y=f(x).)

2.      Что такое область определения функции? (Областью определения функции называют множество всех допустимых значений переменной x.)

3.      Чем является область определения функции геометрически? (Геометрически – это проекция графика функции на ось Ох.)

4.      Что такое множество значений функции? (Множество значений функции — множество всех значений, которые функция принимает на области определения.)

5.      Чем является множество значений функции геометрически? (Геометрически – это проекция графика функции на ось Оy.)

4.     Изучение нового материала

5.     Формирование знаний, умений и навыков

№ 691 (2, 4, 6)

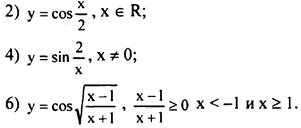
 692 (3, 4, 5)

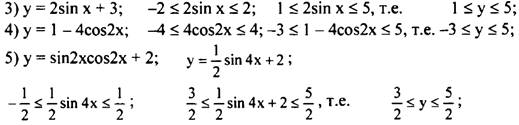
693 (2, 3)

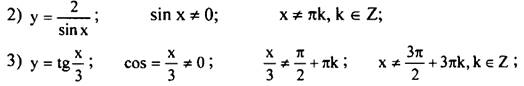
 Доп:  № 694 (1 – 4)

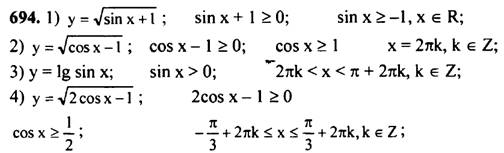
6.     Подведение итогов урока

7.     Домашнее задание     §38, № 691 (1, 3, 5), № 692 (1, 2, 6), № 693 (1, 4)

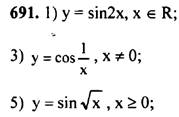
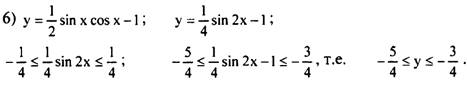
Доп:  № 694 (5, 6)