3 ОПТИМИЗАЦИЯ СЕТЕВЫХ ПЛАНОВ

КОМПЛЕКСА РАБОТ

3.1 Постановка задачи оптимизации

До сих пор мы считали, что время выполнения всех работ  задано. Обычно это не совсем так. Для большинства работ заданным можно считать время некоторого нормального режима выполнения работ, которое будем обозначать D_i. В то же время с помощью привлечения дополнительных сил и средств выполнение работы можно интенсифицировать (ускорить) вплоть до некоторого форсированного режима, при котором время выполнения работ будет равно d_i, т.е.

,                                   (3.1)

где n – число работ сетевого графика, номер последней работы, завершающей комплекс работ; i – номер работы в проекте.

Обычно не составляет большого труда рассчитать стоимость выполнения работ в нормальном и форсированном режимах С_Di и C_di соответственно. Сложней бывает рассчитать промежуточные значения стоимости С _i.

,                                              (3.2)

поэтому зависимость С_i=f(t_i) в первом приближении принимают линейной, которая задается двумя точками (рис. 9).

 ,                                             (3.3)

где .                                                         (3.4)

При появлении возможности изменения времени и стоимости выполнения работ сетевого графика возникает задача оптимизации: как лучше распорядиться имеющимися средствами и временем, чтобы выполнить комплекс работ возможно быстрей и дешевле. Возможны три основные постановки задачи оптимизации сетевого графика:

 

 

 

 

 

 

 

 

 

 

 

1 Задано допустимое время выполнения комплекса работ сетевого графика Т₀.

                                               (3.5)

Необходимо определить длительность и стоимость всех работ  так, чтобы суммарная стоимость С_СГ была минимальна

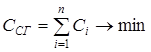 .                            (3.6)

2 Задана допустимая суммарная стоимость выполнения работ сетевого графика С₀

 .                                              (3.7)

Необходимо определить для всех работ значения , при которых время выполнения комплекса работ сетевого графика будет минимальна

 .                                        (3.8)

Задачи в первых двух постановках относятся к задачам линейного программирования и могут решаться симплекс-методом. Однако существует более простой и универсальный алгоритм решения этих задач, который будет описан ниже.

3 Обычно задача ставится в более общем виде: желательно минимизировать не один из показателей при ограничении на другой, а по возможности уменьшить и время, и стоимость, находя между ними некоторый разумный компромисс. При этом, вообще говоря, может иметь место либо одно, либо даже оба ограничения, (3.5), (3.7), ясно что они не должны противоречить друг другу. Наличие ограничений не влияет на метод решения задачи, они могут быть учтены на последнем этапе принятия решения, поэтому при описании алгоритма решения эти ограничения не рассматриваются.

Для решения задач оптимизации по двум показателям (времени и стоимости) целесообразно использовать метод отбрасывания явно неэффективных решений. Общее число решений в ОДР (область допустимых решений) и на ее границах, задаваемых неравенствами (3.1), (3.2), измеряется многими тысячами даже для сравнительно простых сетевых графиков. Цель алгоритма оптимизации состоит в нахождении множества вариантов, лежащих на левой нижней границе области решений, т.е. одновременно минимизирующих и время и стоимость.

Таких вариантов получается несколько и окончательный выбор наилучшего из них относится к компетенции ответственного руководителя комплексом работ и осуществляется с учетом всей совокупности условий и факторов, позволяющих оценить, на какие дополнительные затраты целесообразно пойти для сокращения срока выполнения работ или какое увеличение времени можно допустить, чтобы не понести слишком больших затрат.

В пределах линейной модели найденные точки зависимости оптимальной стоимости С_опт от оптимального времени выполнения работ сетевого графика Т_опт С_опт=f (Т_опт) позволяет восстановить всю зависимость, соединив их отрезками прямых (рис. 13). Следовательно, алгоритм решения задачи в общей постановке позволяет решать задачу и в двух первых постановках (3.5), (3.6), и (3.7), (3.8).

В литературе описаны и другие постановки задачи оптимизации сетевого графика. Предполагается, что сетевой график задан и имеется возможность изменения режимов выполнения работ, увеличивая или уменьшая время их выполнения с экономией средств или увеличением затрат в соответствии с зависимостью (3.3).

Первая задача: требуется уменьшить время выполнения комплекса работ до заданной величины Т₀ с минимальными дополнительными затратами.

Вторая задача: увеличить время выполнения сетевого графика до допустимого значения, но таким образом, чтобы при этом получить максимальную экономию средств.

Третья задача состоит в том, что следует перераспределить имеющиеся средства из некритических работ в критические так, чтобы минимизировать время выполнения комплекса работ.

Нетрудно понять, что все эти задачи легко сводятся к первым двум основным задачам.

 

3.2 Общий алгоритм решения оптимизационной задачи

 

Алгоритм состоит в следующем. В начале рассматривается нормальный режим выполнения работ сетевого графика, т.е. для всех работ принимается

,

где n – число работ.

Затем начинается пошаговое уменьшение (форсирование) времени выполнения отдельных работ и всего комплекса работ таким образом, чтобы удорожание на каждом шаге было минимально возможным. Общая структура алгоритма приведена на рис. 10.

Исходными данными является структурный сетевой график и значения .

Для реализации алгоритма структуру сетевого графика представляют с помощью двух логических матриц: матрицы путей Р и матрицы минимальных сечений S. Путь – это множество последовательных работ, соединяющих первый и последний узлы сетевого графика.

Рис. 10

 

Граф:                                                     Пути:

 

Сечения:

 

 

Рис. 11.

 

Минимальное сечение – это минимальное множество работ, удаление (размыкание) которых из графа рассоединяет начальный и конечный узлы сетевого графика или другое определение, которое более ясно отражает суть оптимизации: это минимальное множество работ, одновременное сокращение времени выполнения которых наверняка приводит к уменьшению времени выполнения сетевого графика. Сечение является минимальным в том смысле, что замыкание любой одной работы образует хотя бы один путь, связывающий начальный и конечный узлы.

Пример минимальных сечений и путей приведены на рис. 11 для простейшего сетевого графика, содержащего всего пять работ. Следует особо обратить внимание на то, что работы сечения, которые опираются только на предшествующие им работы того же сечения, не принадлежат минимальному сечению. В примере (рис. 11) это работа а₃ в третьем минимальном сечении.

Матрица путей составляется следующим образом. Она имеет п столбцов по числу работ сетевого графика и т строк по числу путей.

 

 

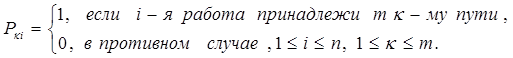
Аналогичным образом составляется матрица минимальных сечений. В ней имеется также п столбцов и l строк по числу минимальных сечений.

 

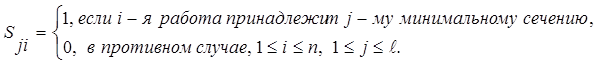
В нашем примере (рис. 11) матрицы имеют следующий вид:

 

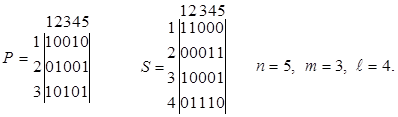
Основная идея алгоритма состоит в выборе на каждом шаге наилучшего способа сокращения длительности выполнения сетевого графика, т.е. выбора минимального сечения, для которого удорожание критических работ минимально. Совершенно очевидно, что вкладывание дополнительных средств в сокращение времени выполнения некритических работ просто бессмысленно, так как эти работы и так имеют резервы времени, и следовательно нужно сокращать только критические работы. Но на критических путях обычно имеется по несколько работ. Какие же сокращать в первую очередь? Фактически же следует сокращать только критические работы минимального сечения.

Для каждой работы показателем скорости удорожания является коэффициент b_i или угол наклона прямой (рис. 12). Чем меньше b_i (угол наклона), тем меньше удорожание на единицу сокращения времени.

Последовательность действий.

 

ЭТАП 0 Подготовительный этап.

1     Задаться матрицей путей Р и матрицей минимальных сечений S.

2     Определить время выполнения работ для каждого пути заданного сетевого графика по формуле:

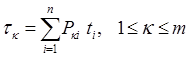.                                   (3.10)

где i – номер работы пути; k – номер пути, m – количество путей.

3     Определить время выполнения сетевого графика Т_СГ как наибольшее из t_к

                                      (3.11)

4     Определить множество критических путей в виде логического вектора V:

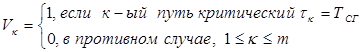                (3.12)

5     Рассчитать стоимость выполнения всех работ по формуле (3.3) и суммарную стоимость выполнения сетевого проекта С_СГ:

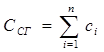,                                         (3.13)

где i – номер работ; n – количество работ сети.

 

ЭТАП 1 Оптимизационный этап.

Может состоять из нескольких шагов, на каждом из которых определяется наилучший способ сокращения длительности выполнения сетевого графика.

1     Рассчитать суммарное удорожание работ для каждого минимального сечения на единицу сокращаемого времени выполнения работ сетевого графика по формуле:

 ,                                (3.14)

где i-номер работы в j-м сечении, k – номер пути.

2     Из всех полученных значений выбрать сечения с минимальным удорожанием:

                                              (3.15)

и установить в них работы, подлежащие уменьшению времени их выполнения (это критические работы, входящие в состав выбранного минимального сечения).

3     Определить величину, на которую можно сократить время выполнения критических работ в выбранных сечениях:

                         (3.16)

где Т_СГ – твремя выполнения сетевого графика;  t_К – время выполнения работ для некритического пути.

Т.е. сокращение времени δ определяется как меньшая величина минимального резерва времени на некритическом пути и минимально возможным уменьшением времени сокращаемых работ до нижней границы d_i.

4  Скорректировать время сокращаемых работ:

t_i=t_i – δ.

5  Определить новую стоимость сокращаемых работ по формуле (3.3):

6  Определить новое значение времени выполнения работ для каждого пути и новое время выполнения сетевого графика по формулам (3.10) и (3.11).

7  Уточнить множество критических путей по формуле (3.12).

8  Осуществить проверку на возможность дальнейшей оптимизации: сократить выполнение сетевого графика более невозможно, если во всех минимальных сечениях имеется хотя бы по одной критической работе, время выполнения которой невозможно уменьшить (достигло своего наименьшего предельного значения).

9  Повторить этап 1, если есть возможность дальнейшей оптимизации сетевого графика по времени и стоимости.

Рассмотрим применение описанного алгоритма на примере (рис.11).

ПРИМЕР На рис.11 дан сетевой граф, содержащий всего пять работ, а также возможные пути и минимальные сечения. В таблице 5 для всех работ сети задано:

– время выполнения работ для нормального режима D_i и для форсированного (предельное минимальное значение) d_i режима.

– стоимость выполнения работ для нормального режима С_Di и для форсированного С_di режима.

Оптимизировать сетевой график по времени и стоимости.

Таблица 5

 

Решение: исходные данные и результаты расчета сводим в таблицу 7. Для наглядности каждый шаг оптимизации отмечаем на графике (рис.13).

 

ЭТАП 0 Подготовительный этап

1     Задаться матрицей путей Р и матрицей минимальных сечений S для указанной сети:

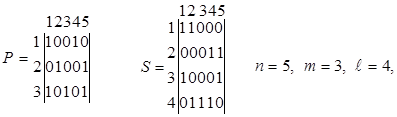
где n – количество работ; m – количество путей;  – количество минимальных сечений.

2     Определить время выполнения работ для каждого пути заданного сетевого графика по формуле (3.10):

                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                   

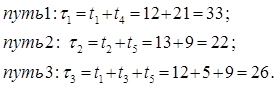
3     Определить время выполнения сетевого графика Т_СГ как наибольшее из t_к

4 Определить множество критических путей в виде логического вектора V:

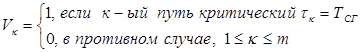 = (1,0,0).

Т. е. критический путь №1, который состоит из следующих работ: a₁ и a₂.

5 Рассчитать стоимость выполнения всех работ по формуле (3.3) и суммарную стоимость выполнения сетевого проекта С_СГ по формуле (3.13):

 

, где

Результат сведем в табл. 6

 Таблица 6

Коэффициенты	Работы
	1	2	3	4	5
ki	49	94	28	53	38
bi	2	6	4	1	2
Сi	25	16	8	32	20

 

Тогда стоимость проекта равна:

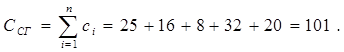
На графике (рис. 13) отмечаем первую точку проекта: (Т_СГ,С_СГ)=(33, 101).

 

ЭТАП 1 Оптимизационный.

ШАГ 1 Определить наилучший способ сокращения длительности выполнения сетевого графика.

Критический путь№1, критические работы a₁ и a₄.

1     Суммарное удорожание работ для каждого минимального сечения, куда входят критические работы, – сечения №1,2,3,4 – на единицу сокращаемого времени выполнения работ сетевого равно (табл.6):

(верхний индекс – номер шага оптимизации сетевого графика; нижний индекс – номер минимального сечения)

2     Из всех полученных значений выбрать сечения с минимальным удорожанием:

, т.е. это минимальные сечения №2 и №4. На этих сечения подлежат уменьшению времени только критические работы, т.е. a₄ (работа a₁ не входит ни в одно из выбранных сечений).

3     Определить величину, на которую можно сократить время работ в выбранных сечениях по формуле (3.16):

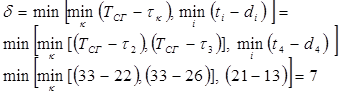
т.е. на 7 ед. времени можно сократить работу a₄.

4 Скорректировать время сокращаемых работ:

Время остальных работ остается без изменения.

5 Новая стоимость сокращаемых работ работ равна (формула 3.3):

Стоимость остальных работ остается без изменения.

6 Определить новое значение времени выполнения работ для каждого пути и новое время выполнения сетевого графика по формулам (3.10) и (3.11):

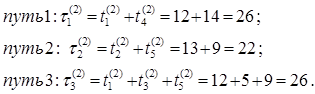
ед. времени на выполнения сетевого проекта.

7     Множество критических путей:

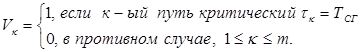 = (1,0,1).

Т. е. критические пути №1и 3. Они состоят из следующих работ: a₁, a₄ и a₅.

8 Рассчитать стоимость выполнения всех работ по формуле (3.3) и суммарную стоимость выполнения сетевого проекта С_СГ по формуле (3.13):

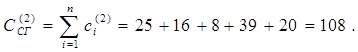
На графике (рис. 13) отмечаем следующую точку проекта: (Т_СГ,С_СГ)=(26, 108).

9 Проверка: дальнейшая оптимизация сетевого графика возможна, т.к. ни для одной критической работы время выполнения работ не достигло своего наименьшего предельного значения, следовательно, есть возможность дальнейшей оптимизации сетевого графика по времени и стоимости.

 

ШАГ 2 Критические пути №1 и 3, критические работы: a₁, a₄ и a₅.

1     Cуммарное удорожание работ для каждого минимального сечения, куда входят критические работы, – сечения №1, 2, 3, 4 – на единицу сокращаемого времени выполнения работ сетевого равно:

2     Из всех полученных значений выбрать сечения с минимальным удорожанием:

, т.е. это минимальное сечение №1. Это сечение содержит критическую работу а₁, которая и будет подлежать сокращению по времени выполнения.

3     Определить величину, на которую можно сократить время работ в выбранных сечениях по формуле (3.16):

 

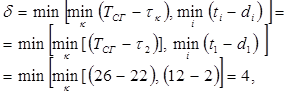
т.е. на 4 ед. времени можно сократить работу a₁.

4  Скорректировать время сокращаемых работ:

Время остальных работ остается без изменения.

5  Новая стоимость сокращаемых работ равна (формула 3.3):

Стоимость остальных работ остается без изменения. Результаты расчета сводим в таблицу 7.

6  Определить новое значение времени выполнения работ для каждого пути и новое время выполнения сетевого графика по формулам (3.10) и (3.11):

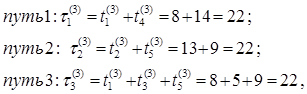
ед. времени на выполнения сетевого проекта.

7     Множество критических путей:

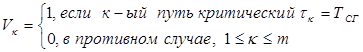 = (1,1,1).

Т. е. критические пути №1,2 и 3. Они состоят из следующих работ: a₁, a₂, a₃, a₄ и a₅.

8  Определяем стоимость выполнения всех работ и суммарную стоимость выполнения сетевого проекта С_СГ после оптимизации на этом шаге:

.

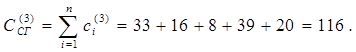На графике (рис. 13) отмечаем следующую точку проекта: (Т_СГ,С_СГ)=(22, 116). Результаты расчета этого шага сводим в табл. 7.

9  Проверка: дальнейшая оптимизация сетевого графика возможна, т.к. есть минимальные сечения, в которых критические работы не достигли своего предельного времени выполнения, следовательно, есть возможность дальнейшей оптимизации сетевого графика по времени и стоимости.

 

ШАГ 3 Критические пути №1, 2 и 3, критические работы: a₁, a₂, a₃, a₄ и a₅.

1     Суммарное удорожание работ для каждого минимального сечения, куда входят критические работы, – сечения №1,2,3,4 – на единицу сокращаемого времени выполнения работ сетевого равно:

2     Из всех полученных значений выбрать сечения с минимальным удорожанием:

, т.е. это минимальное сечение №2. Это сечение содержит критические работы a₄ и a₅, которые и будет подлежать сокращению по времени выполнения.

3     Определяем величину, на которую можно сократить время работ в выбранных сечениях:

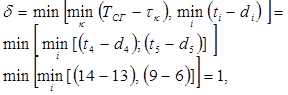
т.е. на 1 ед. времени можно сократить работы a₄ и a₅,.

4  Скорректируем время сокращаемых работ:

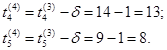
Время остальных работ остается без изменения.

5  Новая стоимость сокращаемых работ равна:

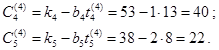
Стоимость остальных работ остается без изменения.

6  Определяем новое значение времени выполнения работ для каждого пути и новое время выполнения сетевого графика:

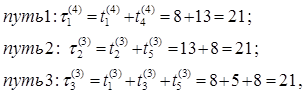
ед. времени на выполнения сетевого проекта.

7  Множество критических путей:

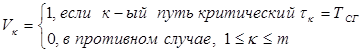 = (1,1,1).

Т. е. критические пути №1, 2 и 3. Они состоят из следующих работ: a₁, a₂, a₃, a₄ и a₅.

8  Определяем стоимость выполнения всех работ и суммарную стоимость выполнения сетевого проекта С_СГ после оптимизации на этом шаге:

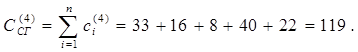
На графике (рис. 13) отмечаем следующую точку проекта: (Т_СГ,С_СГ)=(21, 119). Результаты расчета этого шага сводим в таблицу 7.

9  Проверка: время выполнения работы a₄ достигло своего предельного наименьшего значения, однако дальнейшая оптимизация сетевого графика возможна, т.к. есть минимальные сечения, в которых критические работы еще не достигли своего предельного времени выполнения.

 

ШАГ 4 Критические пути №1,2 и 3, критические работы: a₁, a₂, a₃, a₄ и a₅.

1     Так как время выполнения работы a₄ достигло своего предельного наименьшего значения, то из рассмотрения исключаем минимальные сечения куда входит эта работа, т.е. сечения 2 и 4. Cуммарное удорожание работ для оставшихся минимальных сечений, куда входят критические работы:

2     Из всех полученных значений выбрать сечения с минимальным удорожанием:

, т.е. это минимальное сечение №3. Это сечение содержит критические работы a₁ и a₅, которые и будет подлежать сокращению по времени выполнения.

3     Определяем величину, на которую можно сократить время работ в выбранных сечениях:

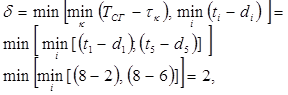
т.е. на 2 ед. времени можно сократить работы a₁ и a₅,.

4  Скорректируем время сокращаемых работ:

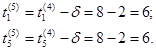
Время остальных работ остается без изменения.

5  Новая стоимость сокращаемых работ равна:

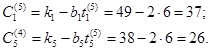
Стоимость остальных работ остается без изменения.

6  Определяем новое значение времени выполнения работ для каждого пути и новое время выполнения сетевого графика:

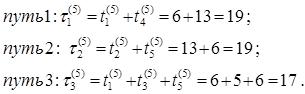
ед. времени на выполнения сетевого проекта.

7  Множество критических путей:

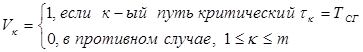 = (1,1,0).

Т. е. критические пути №1 и 2. Они состоят из следующих работ: a₁, a₂, a₃, a₄ и a₅.

8  Определяем стоимость выполнения всех работ и суммарную стоимость выполнения сетевого проекта С_СГ после оптимизации на этом шаге:

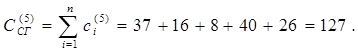
На графике (рис. 13) отмечаем следующую точку проекта: (Т_СГ,С_СГ)=(19, 127). Результаты расчета этого шага сводим в таблицу 7.

9  Проверка: время выполнения работы a₅ достигла своего предельного наименьшего значения на этом шаге оптимизации, однако дальнейшая оптимизация сетевого графика возможна, т.к. есть минимальное сечение, в котором критические работы еще не достигли своего предельного времени выполнения.

 

ШАГ 5 Критические пути №1 и 2, критические работы: a₁, a₂, a₄ и a₅.

Так как время выполнения работ a₄ и a₅ достигло своего предельного наименьшего значения, то из рассмотрения исключаем минимальные сечения, куда входят эти работы, т.е. сечения 2, 3 и 4.

1      Cуммарное удорожание работ для оставшегося минимального сечения:

2     Из всех полученных значений выбрать сечения с минимальным удорожанием:

, т.е. это минимальное сечение №1 содержит критические работы a₁ и a₂, которые и будут подлежать сокращению по времени выполнения.

3     Определяем величину, на которую можно сократить время работ в выбранных сечениях (внимание: появился некритический путь №3, но на нем есть сокращаемая работа, поэтому он не учитывается):

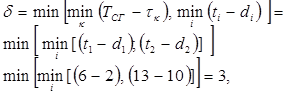
т.е. на 3 ед. времени можно сократить работы a₁ и a₂,.

4  Скорректируем время сокращаемых работ:

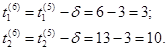
Время остальных работ остается без изменения.

 

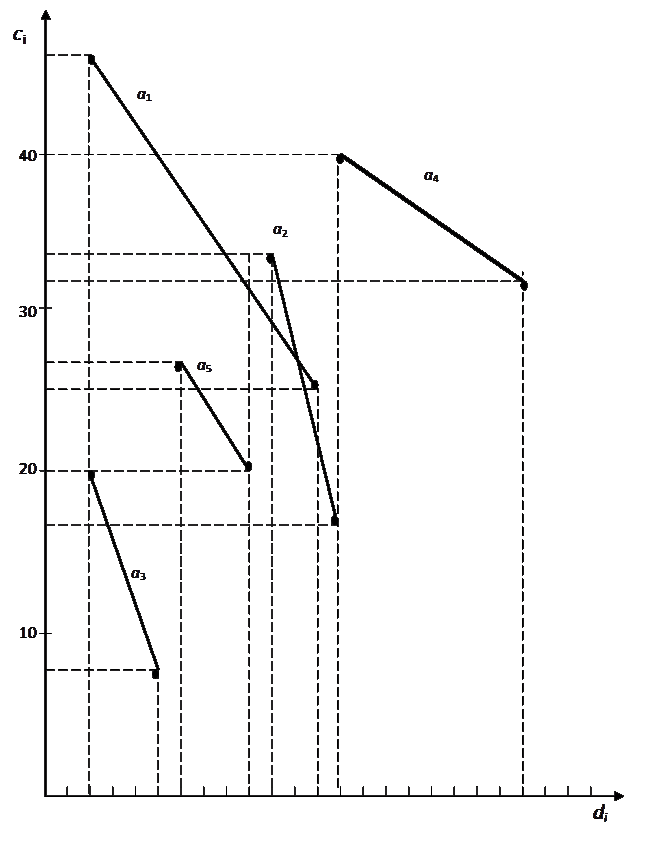Рис.12

 

Рис.13

 

5  Новая стоимость сокращаемых работ равна:

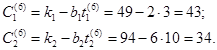
Стоимость остальных работ остается без изменения.

6  Определяем новое значение времени выполнения работ для каждого пути и новое время выполнения сетевого графика:

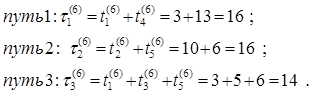
ед. времени на выполнения сетевого проекта.

7  Множество критических путей:

 = (1,1,0).

Т. е. критические пути №1 и 2. Они состоят из следующих работ: a₁, a₂, a₄ и a₅.

8  Определяем стоимость выполнения всех работ и суммарную стоимость выполнения сетевого проекта С_СГ после оптимизации на этом шаге:

На графике (рис. 13) отмечаем следующую точку проекта: (Т_СГ,С_СГ)=(16, 151). Результаты расчета этого шага сводим в таблицу.

9  Проверка: время выполнения работы а₂ достигло своего предельного наименьшего значения на этом шаге оптимизации. Дальнейшая оптимизация сетевого графика невозможна, т.к. нет минимальных сечений, в которых критические работы еще не достигли своего предельного времени выполнения.

Окончательные результаты расчета представлены на рис. 13 и табл.7.

В качестве оптимального примем решение в точке 3, для которой Т_СГ=22, С_СГ=116. Это решение является компромиссным между нормальным – наиболее длительным режимом (Т_СГ=33, С_СГ=101) и форсированным – наиболее дорогостоящим режимом (Т_СГ=16, С_СГ=151).

Сравнение этих режимов показывает, что нормальный режим всего на 13 % дешевле и в полтора раза длительней, форсированный режим при сокращении длительности на 27 % требует увеличения затрат на 30 %. Окончательное решение остается за руководителем комплекса работ.

Для выбранного нами режима на рис. 14 приведен календарный план; составление его не представляет труда, так как все пути и все работы сетевого графика являются критическими.

Таблица 7

№ п/п	Работы					ТСГ ССГ	t1 t2 t3	Номера критических путей	Номер сокращаемого миним. сечения	Номер сокращаемых работ	Сокращение времени d
	t1 c1	t2 c2	t3 c3	t4 c4	t5 c5
1	12 25	13 16	5 8	21 32	9 20	33 101	33 22 26	1	2, 4	4	7
2	12 25	13 16	5 8	14 39	9 20	26 108	26 22 26	1, 3	1	1	4
3	8 33	13 16	5 8	14 39	9 20	22 116	22 22 22	1, 2, 3	2	4, 5	1
4	8 33	13 16	5 8	13 40	8 22	21 119	21 21 21	1, 2, 3	3	1, 5	2
5	6 37	13 16	5 8	13 40	6 26	19 127	19 19 17	1, 2	1	1, 2	3
6	3 43	10 34	5 8	13 40	6 26	16 151	16 16 14	1, 2	–	–	–

 

 

 

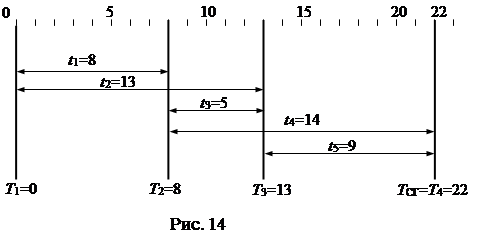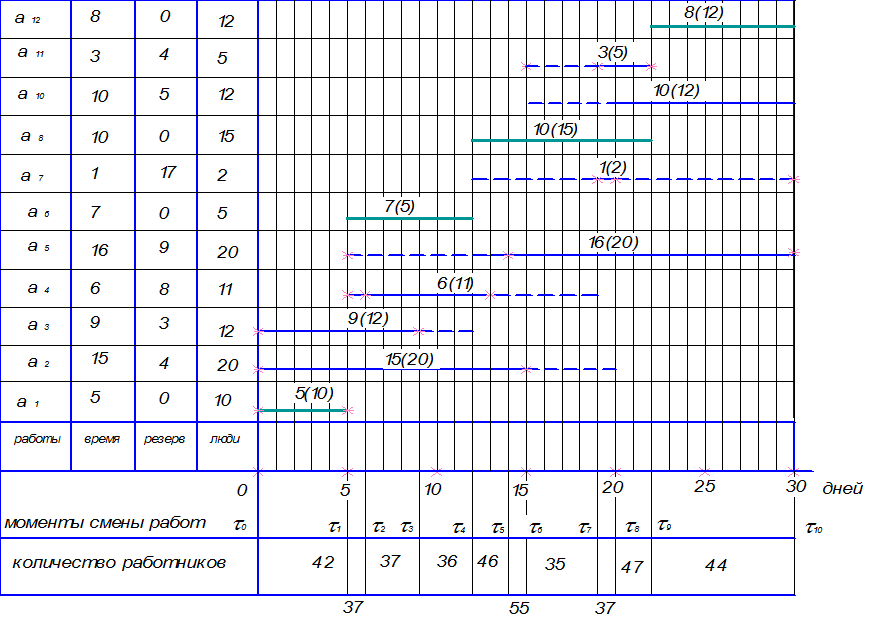Рис. 15

Скачано с www.znanio.ru