Поделиться
ОШИБКИ ПРИ ПЕРЕДАЧЕ ИНФОРМАЦИИ.docx
ОШИБКИ ПРИ ПЕРЕДАЧЕ ИНФОРМАЦИИ*
Когда информация постоянно передается между различными частями компьютера, пересылается от Земли к Луне и об- ратно либо просто сохраняется в устройстве памяти, вероятнее всего, полученная, в конце концов, битовая комбинация бу- дет отличаться от исходной. Частички грязи или жира на магнитной записывающей поверхности, случайная ошибка в работе электронной схемы – все это может вызвать ошибки при записи или чтении данных. Более того, при использовании некото- рых технологий хранения данных фоновое радиационное излучение может изменять битовые комбинации, записанные в основной памяти машины.
Для решения этих проблем было разработано множество технологий кодирования данных, позволяющих обнаруживать и даже исправлять подобные ошибки. В настоящее время эти технологии широко используются при создании внутренних компонентов компьютеров, поэтому они остаются незаметными для пользователей, работающих с машиной. Однако они чрезвычайно важны, и это лишний раз подчеркивает значение результатов выполненных научных исследований. В сущно- сти, большую часть работы по созданию подобных технологий выполнили математики-теоретики. Ниже мы рассмотрим не- которые из тех методов, которые обеспечивают надежность функционирования современных вычислительных машин.
Биты четности. Существует достаточно простой способ определения ошибок, построенный на том принципе, что если каждая обрабатываемая битовая комбинация будет состоять из нечетного количества единиц, то обнаружение комбинации с четным количеством единиц будет свидетельствовать о возникновении ошибки. Чтобы использовать этот принцип, необхо-
 |
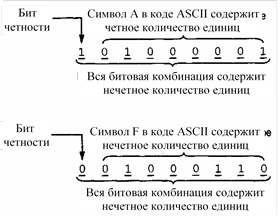Рис. 1.20. Представление символов A и F в коде ASCII
с использованием контрольного бита
с четным количеством единиц будет свидетельствовать об ошибке и сигнализировать, что обрабатываемые данные являются неверными. Описанная выше система контроля четности называется проверкой на нечетность (odd parity), поскольку все обрабатываемые битовые комбинации должны содержать нечетное количество единиц. Кроме того, существует способ, име- нуемый проверкой на четность (even parity). В этом случае все обрабатываемые комбинации должны содержать четное ко- личество единиц, а показателем ошибки является нечетное количество единиц в битовой комбинации.
В наше время использование битов четности является типовым решением для основной памяти машины. Хотя внешне создается впечатление, что компьютеры используют восьмиразрядные ячейки памяти, в действительности они являются де- вятиразрядными, причем девятый бит используется как контрольный. Каждый раз, когда в память записывается некоторая восьмибитовая комбинация, схема управления памятью автоматически добавляет к ней требуемый контрольный бит для по- лучения девятиразрядной комбинации. При считывании информации схема управления памятью подсчитывает количество единиц в полученной комбинации. Если ошибка не обнаруживается, контрольный бит удаляется и образуется исходная восьмиразрядная битовая комбинация. В противном случае схема управления памятью возвращает считанное восьмиразряд- ное значение с указанием, что оно искажено и может отличаться от исходного.
Длинные битовые комбинации часто дополняются группой контрольных битов, образующих контрольный байт. Каж- дый бит в этом байте является контрольным и относится к определенной группе битов, разбросанных по основной битовой комбинации. Например, один контрольный бит может относиться к каждому восьмому биту, начиная с первого, тогда как другой – к каждому восьмому биту, начиная со второго, и т.д. В данном случае легче выявить ошибки, сконцентрированные в одной области исходной комбинации, поскольку их наличие будет контролироваться группой контрольных битов. Различ- ные варианты данного подхода к созданию схем контроля называются методом контрольных сумм и методом использования кода циклического контроля избыточности (CRC).
Коды с исправлением ошибок. Несмотря на то что бит четности является эффективным методом выявления ошибок, он не дает информации, необходимой для исправления возникшей ошибки. Многих удивляет сам факт, что можно разрабо- тать коды с исправлением ошибок, позволяющие не только выявлять ошибки, но и исправлять их.
В конце концов, интуиция подсказывает, что мы не в состоянии исправить ошибку в полученном сообщении, если зара-
 |
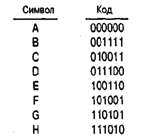Рис. 1.21. Код
с исправлением ошибок
нее не знаем, о чем там идет речь. Тем не менее, существует довольно простой код, позволяющий исправлять возникающие ошибки (рис. 1.21).
Для того чтобы понять принцип действия этого кода, сначала необходимо определить дистанцию Хэмминга (Hamming
distance) между двумя кодовыми комбинациями, которая будет равна количеству битов, отличающихся в этих комбинациях.
Понятие "дистанция Хэмминга" получило свое название в честь Р.В. Хэмминга
(R.W. Hamming), который провел первые исследования в области разработки кодов с исправлением ошибок. Он обра- тился к этой проблеме в 1940-х годах по причине крайней ненадежности существовавших в то время релейных вычисли- тельных машин. Например, дистанция Хэмминга между кодами букв А и В (рис. 1.21) равна четырем, а дистанция Хэмминга между кодами букв В и С равна трем. Важной особенностью этого кода является то, что дистанция Хэмминга между любы- ми двумя комбинациями будет не меньше трех. Если в результате сбоя в каком-либо отдельном бите появится ошибочное значение, то ошибка будет легко установлена, так как получившаяся комбинация не является допустимым кодовым значени- ем. В любой комбинации потребуется изменить не меньше трех битов, прежде чем она вновь станет допустимой.
Если в любой комбинации, показанной на рис. 1.21, возникла одиночная ошибка, то легко можно вычислить ее исход- ное значение. Дело в том, что дистанция Хэмминга для измененной комбинации по отношению к исходной форме будет равна единице, тогда как по отношению к другим разрешенным комбинациям она будет равна не менее чем двум. При деко- дировании некоторого сообщения достаточно просто сравнивать каждую полученную битовую комбинацию с допустимыми комбинациями кода, пока не будет найдена комбинация, находящаяся на дистанции, равной единице, от полученной комби- нации. Найденная допустимая кодовая комбинация принимается за правильный символ, полученный в результате декодиро- вания. Предположим, что получена битовая комбинация 010100. Если сравнить ее с допустимыми битовыми комбинациями кода, то будет получена таблица дистанций, представленная на рис. 1.22. По содержанию этой таблицы можно сделать за- ключение, что поступивший символ – это буква D, так как ее битовая комбинация в наибольшей степени соответствует по- лученной.
Как видите, при использовании кода, представленного на рис. 1.22, действительно
можно обнаружить до двух ошибок в одной комбинации и исправить одну ошибку.
Если использовать код, в котором дистанция Хэмминга между комбинациями
равняется как минимум пяти, то можно было бы обнаруживать до четырех ошибок в
одной комбинации и исправлять до двух ошибок.
Рис. 1.22. Декодирование битовой комбинации 010100
с помощью кода, представленного на рис. 1.21
Естественно, разработка эффективных кодов с достаточно длинными дистанциями Хэмминга является непростой задачей. Для этого требуется знание такой области математики, как алгебраическая теория кодирования, которая является частью линейной алгебры и теории матриц.
Методы коррекции ошибок широко используются в целях повышения надежности вычислительной техники. Например, они используются в драйверах магнитных дисков большой емкости, чтобы снизить вероятность искажения хранимой ин- формации в результате дефектов поверхности диска. Более того, главное отличие между форматом, используемым в звуко- вых компакт-дисках, и форматом CD-ROM, предназначенным для записи компьютерных данных, заключается именно в ис- пользовании кодов с исправлением ошибок. Функция исправления ошибок в формате CD-DA позволяет устранять только одну ошибку на два компакт-диска, и этого вполне достаточно для аудиозаписей. Однако для компаний, поставляющих про- граммное обеспечение, наличие ошибок в 50 % поставляемых ими компакт-дисков является совершенно недопустимым. По- этому в формат CD-ROM включены дополнительные средства, позволяющие снизить вероятность возникновения ошибки до одной на 20 000 компакт-дисков.
1. Приведенные ниже битовые комбинации были закодированы с использованием контроля по нечетности. Укажите комби- нации с ошибками.
а) 10101101; б) 10000001; в) 00000000; г) 11100000; д) 11111111.
2. Могли бы Вы не заметить ошибки в байтах, представленных в первом вопросе? Поясните свой ответ.
3. Какими бы были Ваши ответы на вопросы 1 и 2, если бы в приведенных байтах использовался контроль на четность?
4. Закодируйте предложения в коде ASCII с использованием контроля по нечетности и помещением контрольного бита в старший конец кода каждого символа:
а) Where are you?
б) "How?" Chery lasked.
в) 2 + 3 = 5.
5. Используйте представленный на рис. 1.21 код с исправлением ошибок для декодирования следующих сообщений: а) 001111 100100 001100
б) 010001 000000 001011
в) 011010 110110 100000 011100
6. Используя пятиразрядные битовые комбинации, разработайте для символов A, В, С, D такой код, чтобы дистанция Хэмминга между любыми двумя комбинациями составляла не меньше трех.
(Упражнения, отмеченные звездочкой, относятся к разделам для дополнительного чтения.)
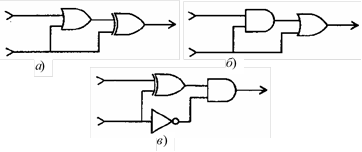
1. Какое выходное значение будет иметь каждая из приведенных ниже схем, если предположить, что на их верхний вход подано значение 1, а на нижний – значение 0.
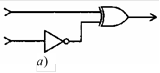
2. 
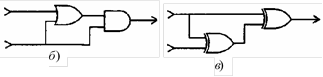Для каждой из приведенных ниже схем укажите комбинации
входных значений, при которых их выходное значение будет равно 1.
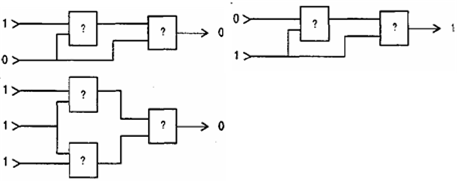
3. В каждой из приведенных ниже схем прямоугольники представляют вентили одного и того же типа. Основываясь на показанных входных и выходных значениях этих схем, определите в каждом случае тип используемого вентиля (AND, OR или XOR).
а)
б)
4.
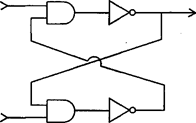
Предполв) им, что на оба входа приведенной ниже цепи
поданы значения 1. Опишите, что произойдет, если на верх-
 |
6. В приведенной ниже таблице представлены адреса и содержимое (в шестнадцатеричной нотации) некоторых ячеек ос- новной памяти машины. Начиная с этого состояния, выполните приведенные инструкции и запишите содержимое этих ячеек памяти после выполнения всех указанных действий.
Адрес
01
02
03
04
Содержимое АВ
53
D6 02
Этап 1. Переместите содержимое ячейки с адресом 03 в ячейку с адресом 00.
Этап 2. Поместите число 01 в ячейку с адресом 02.
Этап 3. Переместите значение, сохраняемое по адресу 01, в ячейку с адресом 03.
6. Сколько ячеек может содержаться в основной памяти компьютера, если адрес каждой ячейки может быть представ- лен тремя шестнадцатеричными числами?
7. Какие комбинации битов представлены следующими шестнадцатеричными обозначениями? а) ВС; б) 67; в) 9А; г) 10; д) 3F.
8. Определите значение старшего значащего бита в битовых комбинациях, представленных следующими шестнадцате- ричными обозначениями:
a) FF; б) 7F; в) 8F; г) 1F.
9. Представьте следующие битовые комбинации в шестнадцатеричной системе счисления: а) 101010101010; б) 110010110111; в) 000011101011.
10. Предположим, что на экране монитора отображены 24 строки, содержащие по 80 символов каждая. Сколько байтов машинной памяти потребуется, чтобы записать в нее все содержимое экрана, представив каждый символ с помощью соот- ветствующего кода ASCII (по одному символу на байт)?
11. Предположим, что выводимое на экран монитора изображение представляет собой прямоугольник, состоящий из 1024 столбцов и 768 строк пикселей. Если для кодирования цвета и яркости каждого пикселя используется 8 бит, то сколько однобайтовых ячеек памяти потребуется для сохранения всего выводимого изображения?
12. а) Назовите два преимущества, которые имеет основная память машины по отношению к дисковым носителям ин- формации.
б) Назовите два преимущества, которые имеют дисковые носители информации по отношению к основной памяти ма- шины.
13. Предположим, вам необходимо подготовить на компьютере курсовую работу объемом приблизительно 40 машино- писных листов. В компьютере имеется дисковое устройство чтения дискет диаметром 31/2 дюйма, емкость которых составля- ет 1,44 Мбайт. Поместится ли ваша курсовая работа на одной такой дискете? Если да, то сколько таких документов может поместиться на одной дискете? Если нет, то сколько дискет потребуется для сохранения вашей курсовой работы?
14. Предположим, что на жестком диске Вашего компьютера, емкость которого составляет 5 Гбайт, осталось только 100 Мбайт дискового пространства. Допустим, вы намерены заменить его жестким диском большей емкости (10 Гбайт) и на время модернизации предполагаете сохранить всю имеющуюся на жестком диске информацию на дискетах размером 31/2 дюйма. Разумно ли это? Поясните свой ответ.
15. Если каждый сектор диска содержит 512 байт, то сколько секторов потребуется для записи одной печатной страни- цы текста, если для хранения одного символа этого текста необходим один байт?
16. Обычная дискета диаметром 31/2 дюйма имеет емкость 1,44 Мбайт. Достаточно ли одной такой дискеты для сохра- нения 400 страниц текста, если каждая страница содержит 3500 символов?
17. Если дискета, которая содержит 16 секторов на каждой дорожке и 512 байт в каждом секторе, вращается со скоро- стью 300 оборотов в минуту, то какой приблизительно будет скорость передачи данных через головку чтения/записи устрой- ства?
18. Если настольный компьютер содержит дисковод, описанный в упражнении 17, и выполняет десять операций за одну микросекунду (миллионную долю секунды), то сколько операций он может выполнить между прохождением двух последо- вательных байтов данных через головку чтения/записи дисковода?
19. Если дискета вращается со скоростью 300 оборотов в минуту, а компьютер способен выполнить 100 операций в микросекунду (миллионная доля секунды), то сколько операций сможет выполнить этот компьютер за время ожидания дос- тупа диска?
20. Сравните время ожидания доступа обычной дискеты, описанной в упражнении 19, и время ожидания доступа жест- кого диска со скоростью вращения 60 оборотов в секунду.
21. Каким будет среднее время доступа жесткого диска, вращающегося со скоростью 60 оборотов в секунду, если его время поиска равно 10 миллисекундам?
22. Предположим, что машинистка может непрерывно день за днем печатать текст со скоростью 60 слов в минуту. Сколько времени потребуется ей, чтобы заполнить компакт-диск емкостью 640 Мбайт? Будем считать, что каждое слово состоит из пяти букв, а для сохранения каждой буквы требуется один байт.
23. Ниже приведен текст сообщения, представленного в кодах ASCII. О чем говорится в этом сообщении?
|
01010111 |
01101000 |
01100001 |
|
01110100 |
00100000 |
01100100 |
|
01101111 |
01100101 |
01110011 |
|
00100000 |
01101001 |
01110100 |
|
00100000 |
01110011 |
00110001 |
|
01111001 |
00111111 |
|
24. Ниже приведен текст сообщения, представленного в кодах ASCII. В этой кодировке на один символ приходится один байт, который в этом упражнении представлен в шестнадцатеричной системе счисления. Декодируйте этот текст.
68657861646563696D616C
25. Закодируйте приведенные ниже выражения в кодах ASCII, используя один байт на один символ. а) 100/5 = 20.
б) То be or not to be?
в) The total cost is $7.25.
26. Представьте ответ из упражнения 25 в шестнадцатеричной системе счисления.
27. Перечислите двоичные представления для целых чисел от 6 до 16.
28. а) Запишите число 13, представив цифры 1 и 3 в коде ASCII;
б) Запишите число 13 в двоичной системе счисления.
29. В двоичном представлении каких чисел содержится только один единичный бит? Приведите двоичные представле- ния для шести наименьших чисел такого вида.
30. Преобразуйте приведенные ниже двоичные числа в эквивалентные десятичные значения: а) 111; б) 0001; в) 11101;
г) 10001; д) 10111; е) 000000;
де:
ж) 100; з) 1000; и) 10000;
к) 11001; л) 11010; м) 11011.
31. Представьте следующие десятичные числа в двоичном представлении:
а) 7; б) 12; в) 16; г) 15; д) 33.
32. Представьте в десятичной системе счисления приведенные ниже числа, записанные в двоичном дополнительном ко-
а) 10000; б) 10011; в) 01104; г) 01111; д) 10111.
33. Представьте приведенные ниже десятичные числа в двоичном дополнительном коде разрядностью 7 битов: а) 12; б) –12; в) –1; г) 0; д) 8.
34. Выполните приведенные ниже операции сложения, полагая, что строки битов представляют числа в двоичном до-
полнительном коде. Укажите, когда полученный результат будет ошибочным из-за переполнения:
а) + 00101 ; б) + 01111 ; в) + 11111 ; г) + 10111 ; д) + 00111 ;
01000
00001
00001
11010
00111
е) + 00111 ; ж) +11111 ; з) + 01010 ; и) + 01000 ; к) + 01010 .
01100
11111
10101
01000
00011
35. Решите приведенные ниже задачи посредством перевода десятичных чисел в двоичный дополнительный код (дли- ной 5 бит). Преобразуйте операции вычитания в эквивалентные операции сложения, а затем выполните суммирование. Про- верьте полученные ответы, преобразовав их в десятичную систему счисления (не забывайте о возможности появления оши- бок переполнения):
а) + 7 ; б) - 7 ; в) -12 ; г) - 8 ; д) + 12 ; е) + 4 .
 |
|
 |
|
|
 |
36*. Преобразуйте приведенные ниже числа, представленные в двоичной нотации с избытком шестнадцать, в десятич- ную форму:
а) 10000; б) 10011; в) 01101; г) 01111; д) 10111.
37*. Представьте приведенные ниже десятичные числа в двоичной нотации с избытком четыре: а) 0; б) 3; в) –3; г) –1; д) 1.
38*. Какие из перечисленных ниже битовых комбинаций не являются допустимыми значениями в двоичной нотации с избытком шестнадцать?
а) 01001; б) 101; в) 010101; г) 00000;
д) 1000; е) 000000; ж) 1111.
39*. Запишите в десятичной системе счисления приведенные ниже числа в двоичном представлении: а) 11.001; б) 100.1101; в) 0.0101; г) 1.0; д) 10.01.
40*. Запишите приведенные ниже числа в двоичной системе счисления:
а) 5 ¾; б) 1/16; в) 7 7/8; г) 11/4; д) 65/8.
41*. Декодируйте следующие битовые комбинации в формате с плавающей точкой: а) 01011100; б) 11001000; в) 00101010; г) 10111001.
42*. Закодируйте приведенные ниже числа, используя восьмиразрядный формат с плавающей точкой. Укажите на ошибки усечения:
a) 1/2; б) 71/2 ; в) –33/4; г) 3/32; д) 31/32.
43*. Какое наилучшее приближение для значения квадратного корня из числа 2 может быть представлено в восьмираз- рядном формате с плавающей точкой? Какое число мы получим, если это приближенное представление корня будет возве- дено в квадрат в машине, использующей указанный формат с плавающей точкой?
44*. Какое наилучшее приближение для значения числа 1/10 может быть достигнуто в восьмиразрядном формате с пла- вающей точкой?
45*. Объясните, как могут возникнуть ошибки, если измерения, выполненные с использованием метрической системы, сохраняются в формате с плавающей точкой. Например, что произойдет, если значение 110 сантиметров будет записано в метрах?
46*. Используйте восьмиразрядный формат с плавающей точкой для вычисления следующей операции суммирования: 1/8 + 1/8 + 1/8 + 21/2; при условии, что она выполняется слева направо. Что изменится в полученном результате, если вычисле- ния производить справа налево?
47*. Какой ответ получит машина при вычислении приведенных ниже примеров суммирования, если в ней использует- ся восьмиразрядный формат с плавающей точкой?
а) 11/2 + 3/16 = б) 31/4 + 11/8 = в) 21/4 + 11/8 =
48*. Для каждого приведенного ниже примера преобразуйте битовые комбинации (интерпретируя их как числа в формате с плавающей точкой) в десятичные значения, выполните сложение, а затем закодируйте ответ в тот же формат с плавающей точкой. Укажите на ошибки усечения.
а) + 01011100 ; б) + 01101010 ; в) + 01111000 ; г) + 01011000 .
01101000
00111000
00011000
01011000
49*. Одна из двух битовых комбинаций 01011 и 11011 представляет некоторое число в двоичной нотации с избытком шестнадцать, а другая – это же число в двоичном дополнительном коде.
а) Что можно сказать относительно этого закодированного значения?
б) Какая взаимосвязь существует между комбинацией битов, представляющей число в двоичном дополнительном коде, и комбинацией битов, представляющей это же число в двоичной нотации с избытком, если в обоих случаях используется один и тот же размер комбинации?
50*. Три битовые комбинации 01101000, 10000010 и 00000010 представляют одно и то же число, записанное в разных форматах: двоичном дополнительном коде, двоичной нотации с избытком и восьмиразрядном формате с плавающей точкой; однако не обязательно в указанном порядке. Определите это число и укажите, какая из битовых комбинаций принадлежит к каждому из перечисленных форматов.
51*. Каждая из приведенных ниже строк битов представляет одно и то же число, записанное в различных системах ко- дирования, обсу-ждавшихся нами выше. Определите каждое из чисел и укажите использованную в каждом случае систему кодирования.
а) 111110100 011 1011
б) 11111101 01111101 11101100
в) 10100010 01101000
52*. Какие из приведенных ниже чисел невозможно точно представить в формате с плавающей точкой? а) 6 1/2; б) 9; в) 13/16; г) 17/32; д) 15/16.
53*. Если увеличить длину битовой строки, используемой для представления целых чисел в двоичной системе, от четы- рех до восьми бит, то какие изменения вызовет это действие в значении наибольшего целого числа, которое может быть представлено этой строкой? Каков будет ответ при использовании двоичного дополнительного кода?
54*. Каким будет шестнадцатеричное представление наибольшего адреса памяти, если размер этой памяти составляет 4
Мбайт и каждая ячейка имеет длину один байт.
55*. Приведенное ниже сообщение было сжато по методу LZ77. Распакуйте это сообщение. 0100101 (4, 3, 0) (8, 7, 1) (17, 9, 1) (8, 6, 1)
56*. Ниже приведена часть сообщения, закодированного по методу LZ77. Исходя из содержащейся в данном представ- лении информации, определите длину исходного сообщения.
abg (_,3, b)(_,6, g)
57*. Запишите последовательность инструкций, поясняющих способ сжатия сообщений по методу LZ77.
58*. Запишите последовательность инструкций, поясняющих способ распаковки сообщений, сжатых по методу LZ77. 59*. Закодируйте следующие выражения в кодах ASCII, используя один байт на символ. Используйте старший бит каж-
дого байта в качестве контрольного бита (по нечету): а) 100/5 = 20;
б) То be or not to be?
в) The total cost is $7.25.
60*. Следующее сообщение было передано с использованием контрольного бита (по нечету) в каждой короткой строке битов. В каких строках имеются ошибки?
|
11011 |
01011 |
10110 |
00000 |
11111 |
10101 |
|
10001 |
00100 |
01110 |
|
|
|
61*. Предположим, что 24-разрядный код создан посредством представления каждого символа с помощью трех после- довательных копий его ASCII-кода (например, символ А будет представлен строкой битов 010000010100000101000001). Ка- кие возможности исправления ошибок допускает этот код?
62*. Для декодирования приведенных ниже слов используйте код с исправлением ошибок, представленный на рис. 1.21:
а) 111010 110110;
б) 101000 100000 001100;
в) 011101 000110 000000 010100;
г) 010010 001000 001110 101111;
д) 000000 110111 100110;
е) 010011 000000 101001 100110.
63*. Используя вентили, разработайте такую схему с четырьмя входами и одним выходом, чтобы значение на выходе было равно нулю или единице, в зависимости от того, является ли четырехразрядная комбинация на входах этой схемы чет- ной или нечетной.
Скачано с www.znanio.ru
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.
