Поделиться
Л2-00865.docx
Основные логические операции
Каждая логическая связка рассматривается как операция, ре- зультат которой зависит от значений входящих в неѐ переменных (то есть высказываний). Для упрощения записи вместо слов «истина» и
«ложь» используют двоичные цифры: «истина» = 1, «ложь» = 0. Ос-
новные логические операции и их результаты при разных значениях высказываний приведены в табл.2.1.
Таблица
2.1 Основные логические операции (иерархия сверху вниз):
|
Название |
Обозначение |
Результат |
|
Отрицание, инверсия (связка «не») |
А, |
А = 0 А = 1 А = 1 А = 0 |
|
Конъюнкция, лог. умножение (связ- ка «и») |
А В, А & В, А ^ В |
А = 1, В = 1 А В = 1, в остальных случаях – = 0 |
|
Дизъюнкция, лог. Сложение (связка «или» |
А v В, А + В |
А = 0, В = 0 А v В = 0, в остальных случаях – = 1 |
|
|
|
|
|
Импликация (связки «если…, то», «из… следует», … влечѐт…» |
А В |
А = 1, В = 0, то А В = 0, в остальных случаях = 1 |
|
Эквиваленция, двойная импликация (связки «тогда и только тогда», «необходимо и достаточно», «…равносильно…», |
А В; А В |
А = 1, В = 1 А В = 1 А = 0, В = 0 А В = 1 А = 1, В = 0 А В = 0 А = 0, В = 1 А В = 0 |
Анализ составных логических высказываний удобно делать
с помощью таблиц истинности.
В них представляют все возможные комбинации
значений элементарных высказываний, которые входят в составное, и его результирующее значения для каждой из них.
При- меры:
 |
 |
 |
 |
||||
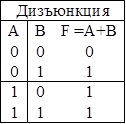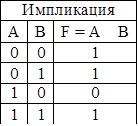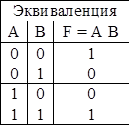Анализ логического высказывания А и не В и не А (A
|
А |
В |
Y1 = А |
Y2 = В |
Y3 = А Y2 |
Y4 = Y3 Y1 |
|
0 |
0 |
1 |
1 |
0 |
0 |
|
0 |
1 |
1 |
0 |
0 |
0 |
|
1 |
0 |
0 |
1 |
1 |
0 |
|
1 |
1 |
0 |
0 |
0 |
0 |
Ответ: выражение тождественно ложно.
Анализ логического высказывания А и не А или В (A А v B)
|
А |
В |
Y1 = А |
Y2 = А Y1 |
Y3 = Y2 v В |
|
0 |
0 |
1 |
0 |
0 |
|
0 |
1 |
1 |
0 |
1 |
|
1 |
0 |
0 |
0 |
0 |
|
1 |
1 |
0 |
0 |
1 |
Ответ: значение выражения совпадает со значением В при лю- бом А.
Также как и для чисел, существуют законы, позволяющие про- изводить тождественные преобразования сложных логических выра- жений к более понятному и удобному виду.
Задание: представить в символах логики высказывание «Если завтра будет дождь, то я возьму зонтик или никуда не пойду».
Ответ: А = «Завтра будет дождь»; В = «Я возьму зонтик»;
С =
«Я никуда не пойду». А (В v С)
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.
