
ОСНОВНЫЕ ЗАДАЧИ ТЕОРИИ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ И УПРАВЛЕНИЯ
Как и любые технические устройства, системы автоматического регулирования и управления в первую очередь должны удовлетворять целому ряду требований общетехнического характера, к которым относятся надежность, помехозащищенность, удобство эксплуатации, технологичность конструкции, минимальная стоимость, заданные вес и габариты и др.
Кроме общетехнических требований, к системам регулирования и управления предъявляется еще и целый ряд других требований, связанных со спецификой задач, решаемых такими системами. Среди них основное место занимают требования по точности регулирования и управления. Применительно к САР требования по точности регламентируют величину ошибки (1.2), которая при любых (оговоренных в задании на проектирование) условиях работы системы не должна превосходить заданной величины.
Как всякие динамические системы, системы регулирования могут работать в двух основных режимах: установившемся и неустановившемся. Неустановившийся режим работы САР часто называется переходным, или динамическим, режимом. Он может быть вызван либо изменением внешних воздействий, либо изменением параметров САР, либо совместным действием обоих этих факторов. Здесь и далее под параметрами системы понимаются такие данные регулятора и объекта регулирования, как передаточные числа, коэффициенты усиления, постоянные времени, моменты инерции, коэффициенты жесткости пружин, емкости, индуктивности и сопротивления электрических цепей и т. д.
Таким образом, в общем случае ошибка САР
![]()
где ![]() — ошибки САР в установившемся и
переходном режимах соответственно.
— ошибки САР в установившемся и
переходном режимах соответственно.
Формула (1.41)
показывает, что требования, предъявляемые к точности работы САР, могут быть
разбиты на требования по точности в установившихся режимах, ограничивающие
ошибку ![]() и
требования по точности в переходных режимах (требования к динамике САР),
накладывающие ограничения на ошибку
и
требования по точности в переходных режимах (требования к динамике САР),
накладывающие ограничения на ошибку ![]()
Возмущения, действующие на систему регулирования, обычно представляют собой непрерывные функции времени, закон изменения которых трудно предугадать. В системах программного регулирования и в следящих системах, кроме того, изменяется во времени и задающее воздействие. Поэтому основным режимом работы любой САР является неустановившийся, переходный режим. Отсюда следует, что ограничиваться рассмотрением только установившихся режимов работы
автоматических систем (как это делалось в предыдущих параграфах при рассмотрении принципа действия отдельных систем регулирования) нельзя. При исследовании систем регулирования следует рассматривать совместно поведение САР как в установившихся, так и в переходных режимах. Очевидно, что поведение САР как в статике, так и в динамике существенным образом зависит от того, каким образом изменяются во времени внешние воздействия, приложенные к системе. Здесь возникает трудность принципиального характера, которая заключается в том, что реальные законы изменения внешних воздействий заранее, как правило, неизвестны, т. е. представляют собой случайные функции времени. Чтобы обойти эту трудность, при исследовании САР часто ориентируются на так называемые типовые законы изменения внешних воздействий, в качестве которых принимают либо наиболее вероятные, либо наиболее неблагоприятные законы изменения задающего и возмущающего воздействий.
Весьма часто в качестве типовых принимают полиномиальные воздействия:
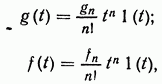
где ![]() — натуральное число;
— натуральное число; ![]() — постоянные величины;
— постоянные величины;
![]()
— так называемая единичная ступенчатая функция.
При ![]() соотношения (1.42) и (1.43) определяют
ступенчатые типовые воздействия:
соотношения (1.42) и (1.43) определяют
ступенчатые типовые воздействия:
![]()
при ![]() — типовые воздействия, изменяющиеся с
постоянной скоростью:
— типовые воздействия, изменяющиеся с
постоянной скоростью:
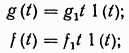
при ![]() — типовые воздействия, меняющиеся с
постоянным ускорением:
— типовые воздействия, меняющиеся с
постоянным ускорением:
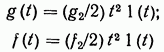
Воздействию (1.45) физически соответствует, например, процесс перенастройки системы автоматической стабилизации на новое
значение регулируемой величины, внезапный поворот командной оси следящей системы на постоянный угол и т. д. (рис. 1.55, а). Воздействие (1.46) характеризует скачкообразное увеличение или уменьшение момента нагрузки в системах регулирования скорости вращения, мгновенное подключение или отключение группы потребителей энергии в системах регулирования напряжения электрогенераторов и т. д.
Воздействия (1.47)
и (1.49) часто используются при исследовании следящих систем воспроизведения
угла и физически соответствуют вращению командной оси с постоянной скоростью ![]() или с постоянным ускорением
или с постоянным ускорением ![]() (рис. 1.55, б, в).
(рис. 1.55, б, в).
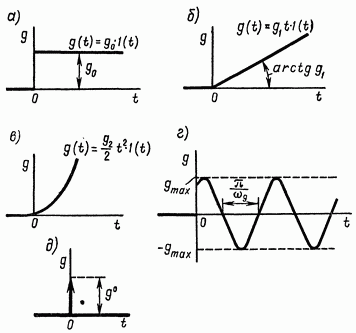
Рис. 1.55. Типовые законы изменения задающего воздействия
Кроме полиномиальных, часто применяются гармонические типовые воздействия:
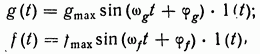
которые достаточно
полно характеризуют физику работы САР, функционирующих в условиях качки,
сильных вибраций и т. д. (рис. 1.55, г). В формулах (1.51) и ![]() — амплитуды гармонических сигналов;
— амплитуды гармонических сигналов; ![]() — их круговые частоты;
— их круговые частоты; ![]() начальные фазовые сдвиги.
начальные фазовые сдвиги.
Далее показано, что гармонические воздействия позволяют весьма полно вскрыть основные свойства САР. Вследствие этого воздействия (1.51) и (1.52) широко применяются и для систем, работающих в условиях непериодических воздействий.
Момент приложения
внешнего воздействия к системе в теории автоматического регулирования обычно
принимается за нуль отсчета времени. При таком подходе все внешние воздействия
для отрицательных моментов времени ![]() считаются равными нулю. Чтобы
подчеркнуть это обстоятельство, в аналитические выражения для внешних
воздействий в качестве множителя вводят единичную ступенчатую функцию
(1.44).
считаются равными нулю. Чтобы
подчеркнуть это обстоятельство, в аналитические выражения для внешних
воздействий в качестве множителя вводят единичную ступенчатую функцию
(1.44).
В некоторых случаях в качестве типовых воздействий выбираются воздействия:
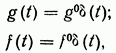
где так называемая единичная дельта-функция
![]()
обладает тем свойством, что
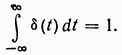
Дельта-функция
представляет собой математическую идеализацию импульса бесконечно малой
длительности, имеющего конечную площадь, равную единице, и относится к числу
функций специального класса, называемых обобщенными ![]()
Воздействия вида (1.53) и (1.54) хорошо отвечают физике работы систем, функционирующих в условиях импульсных возмущений. Графическое изображение таких воздействий затруднительно. На основании соотношения (1.56) «площади» импульсов (1.53) и (1.54) определяются следующими формулами:
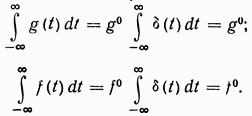
Поэтому
воздействия (1.53) и (1.54) удобно графически изображать стрелками, длины
которых в принятом масштабе характеризуют величины ![]() (рис. 1.55, д).
(рис. 1.55, д).
Выше перечислены лишь простейшие из возможных типовых воздействий. В отдельных случаях эти воздействия могут иметь весьма сложную форму, определяемую экспериментальным путем.
Каким бы ни было выбранное типовое воздействие, оно всегда вызывает в САР некоторый переходный процесс. Если этот процесс затухает, то после его окончания система приходит в установившееся состояние.
В гл. 5 и 9 показано, что вопросы оценки точности работы САР в установившихся режимах решаются сравнительно просто как при типовых, так и при случайных воздействиях.
Наиболее трудной задачей является изучение поведения САР в неустановившихся режимах, в динамике. Объясняется это тем, что современные системы регулирования представляют собой весьма сложные динамические системы со многими степенями свободы. Для упрощения исследование динамики САР обычно разбивают на иссле дование устойчивости и исследование качества переходных процессов.
Системы регулирования, работающие по отклонению, вследствие самого принципа их действия, благодаря которому часть энергии с их выхода передается на вход, склонны к колебаниям. При неудачном выборе структуры или параметров регулятора обратная связь может превратиться из средства подавления колебаний и уменьшения ошибки в средство генерации колебаний и увеличения ошибки.
Для удовлетворительной работы САР прежде всего необходимо, чтобы возникающие по тем или иным причинам начальные отклонения регулируемой величины от требуемого закона ее изменения с течением времени стремились к нулю. Системы регулирования, обладающие этим свойством, называются устойчивыми системами. В устойчивых системах переходные процессы с течением времени затухают. Неустойчивые системы характеризуются расходящимся переходным процессом и для практического применения в подавляющем большинстве случаев непригодны.
Из сказанного ясно, что любая САР прежде всего должна быть исследована на устойчивость. При этом устойчивость системы должна быть обеспечена с некоторым запасом, предусматривающим возможные изменения параметров системы в процессе ее эксплуатации.
Выполнение требований по устойчивости гарантирует лишь факт затухания переходных процессов с течением времени. Время затухания и форма переходных процессов при этом могут быть любыми. Поэтому устойчивость является необходимым, но далеко не достаточным условием практической пригодности САР. Кроме устойчивости любая система регулирования должна обладать еще требуемым качеством работы.
Качество САР
характеризует ее поведение в неустановившихся режимах. Достаточно полное
представление о качестве САР можно получить, располагая кривой изменения во
времени регулируемой величины ![]() или
ошибки
или
ошибки ![]() при
тех или иных типовых воздействиях. В общем случае ввиду сложности современных
систем регулирования теоретическое построение процессов
при
тех или иных типовых воздействиях. В общем случае ввиду сложности современных
систем регулирования теоретическое построение процессов ![]() или
или ![]() требует достаточно трудоемких
вычислений. В связи с этим при исследовании качества САР обычно широко
используются различные критерии качества, представляющие собой числовые
характеристики, зависящие от структуры и параметров системы. При таком подходе
система регулирования считается обладающей требуемым качеством работы, если
критерии качества лежат в заданных пределах. Сами критерии
требует достаточно трудоемких
вычислений. В связи с этим при исследовании качества САР обычно широко
используются различные критерии качества, представляющие собой числовые
характеристики, зависящие от структуры и параметров системы. При таком подходе
система регулирования считается обладающей требуемым качеством работы, если
критерии качества лежат в заданных пределах. Сами критерии
качества могут быть весьма разнообразными, причем их выбор зависит от конкретных условий работы САР (см. гл. 5)
Исследование устойчивости и качества САР должно производиться в тесной связи с исследованием ее поведения в установившихся режимах. Во многих случаях мероприятия, направленные на уменьшение установившейся ошибки САР, приводят к резкому ухудшению динамических свойств САР, и наоборот.
Из сказанного выше следует, что основными проблемами теории автоматического регулирования являются: а) проблема точности работы САР в установившихся режимах, б) проблема устойчивости, в) проблема качества.
Всестороннее изучение этих проблем и разработка на основе этого изучения инженерных методов анализа и синтеза САР являются важнейшими задачами теории регулирования. При этом под анализом понимается исследование готовой САР с целью определения ее свойств и путей их улучшения, а под синтезом — проектирование САР, удовлетворяющей поставленным требованиям.
Наиболее сложной и наиболее важной для практики является задача синтеза систем автоматического регулирования. Обычно ее решение содержит следующие этапы.
1. Изучение объекта регулирования, условий его работы и основных возмущений.
2. Формулировка требований, предъявляемых к САР.
3. Выбор принципа регулирования и первоначальной схемы регулятора.
4. Выбор элементов регулятора с учетом требований, предъявляемых к их мощности и надежности, а также эксплуатационных требований.
5. Выбор и расчет элементов регулятора и их параметров на основе требований, предъявляемых к статическим и динамическим свойствам системы.
6. Экспериментальное исследование САР и ее отдельных частей в лабораторных условиях и внесение коррективов в первоначальную схему регулятора.
7. Изготовление и монтаж САР.
8. Наладка САР в реальных условиях ее работы.
9. Опытная эксплуатация САР.
Обычно улучшение свойств системы регулирования достигается ценой усложнения схемы регулятора. В связи с этим проектирование САР сводится к нахождению разумного компромисса между стремлением получить возможно более высокое качество работы и стремлением решить эту задачу наиболее простыми средствами.
При проектировании САР в равной степени используются как теоретические, так и экспериментальные методы исследования. Применение теоретических методов анализа и синтеза требует предварительного математического описания САР. Систему уравнений, описывающих работу системы регулирования, часто называют математической моделью САР.
Обычно математическое описание САР приводит к системе дифференциальных, интегральных, дифференциально-разностных или разностных уравнений.
В зависимости от характера математической модели все системы регулирования и управления принято делить на обыкновенные линейные, особые линейные и нелинейные.
Обыкновенными линейными (или линейными стационарными) называются САР, работа которых с достаточной степенью точности может быть описана системой обыкновенных линейных дифференциальных уравнений с постоянными коэффициентами.
Особыми линейными называются САР, математическое описание которых приводит к системе линейных уравнений, отличных от обыкновенных линейных дифференциальных уравнений с постоянными коэффициентами. К ним относятся линейные системы с переменными параметрами (или линейные нестационарные системы), описываемые обыкновенными линейными дифференциальными уравнениями с переменными во времени коэффициентами; линейные системы с распределенными параметрами, описываемые линейными дифференциальными уравнениями в частных производных; линейные системы с запаздыванием, математической моделью которых является система линейных дифференциальных уравнений с запаздывающим аргументом, и линейные импульсные системы, математическое описание работы которых дает систему линейных разностных уравнений.
Нелинейными называются САР, работа которых описывается нелинейными уравнениями того или иного вида (дифференциальными, интегральными, разностными и др.).
Классификация САР в зависимости от характера описывающих их уравнений в значительной степени условна. Одна и та же система регулирования может быть описана как линейными, так и нелинейными уравнениями в зависимости от допущений, принятых при составлении уравнений САР, и целей исследования.
Исследование линейных систем существенно проще, чем нелинейных, так как для них справедлив принцип наложения (суперпозиции), согласно которому реакция линейной системы на любую комбинацию внешних воздействий равна сумме реакций на каждое из этих воздействий, взятое по отдельности. Принцип наложения позволяет создать общую теорию линейных систем, описываемых линейными дифференциальными и разностными уравнениями любого порядка.
Для нелинейных систем принцип суперпозиции несправедлив, и общая теория нелинейных САР отсутствует. Поэтому в тех случаях, когда это возможно, при математическом описании работы САР пренебрегают различного рода нелинейностями, стараясь получить математическую модель в виде системы линейных уравнений. Сделать это удается далеко не всегда. Конечным критерием правильности допущений, принятых при математическом описании САР, является практика. Если результаты экспериментального исследования САР, спроектированной на основании той или иной математической модели, дают существенные расхождения с теорией, то это обычно свидетельствует о некорректности допущений, принятых при
математическом описании САР. Очень часто причиной расхождения результатов эксперимента с теорией является влияние различных нелинейных факторов, не учтенных при составлении математической модели системы.
Сложность современных систем регулирования имеет своим следствием и сложность их математических моделей, представляющих собой в большинстве случаев системы дифференциальных и иных уравнений достаточно высокого порядка. Поэтому теория автоматического регулирования, являющаяся прикладной инженерной дисциплиной, вынуждена, тем не менее, использовать весьма сложный математический аппарат. Возникающие при исследовании САР трудности математического характера приводят к тому, что результаты теоретического изучения работы систем регулирования (как в плане анализа, так и в плане синтеза) имеют достаточно приближенный характер. Для уточнения результатов и окончательного выбора параметров систем регулирования необходимо привлечение средств вычислительной техники (вычислительных машин непрерывного действия и универсальных цифровых вычислительных машин) с последующей окончательной доводкой и настройкой регуляторов в реальных условиях.
В настоящее время теория автоматического регулирования представляет собой достаточно развитую и в значительной степени сложившуюся дисциплину, обеспечивающую решение большинства задач, связанных с анализом и синтезом систем регулирования. Однако практика автоматизации ставит перед теорией автоматического регулирования новые и все более сложные задачи, и поэтому перспективы ее дальнейшего развития несомненны.
Теория автоматического регулирования сыграла большую роль в становлении и развитии теории автоматического управления. Автоматическое регулирование представляет собой наиболее совершенный вид автоматики в период частичной автоматизации, когда технические средства автоматики осуществляют лишь простые функции управления, связанные с сигнализацией, контролем, блокировкой, защитой и отработкой решений, принятых человеком-оператором в виде задающих воздействий (настроек, программ регулирования и т. д.).
В настоящее время на смену частичной приходит комплексная автоматизация, при которой кроме простых функций управления автоматизируются и более сложные, связанные с самой выработкой задающих воздействий и программ регулирования. При частичной автоматизации сложные автоматические системы обычно состоят из отдельных систем регулирования, взаимная координация работы которых осуществляется человеком. При комплексной автоматизации возникает необходимость в автоматической координации действий отдельных систем регулирования и, следовательно, в создании сложных взаимосвязанных систем автоматического управления.
В основе построения комплексно автоматизированных систем управления лежит так называемый иерархический принцип, который заключается в том, что сложные системы управления образуются из ряда ступеней. На первой ступени автоматизируются сравнительно
простые локальные процессы управления; на второй — процессы управления, имеющие более сложный и общий характер, и т. д. При таком подходе теория автоматического регулирования является основой построения первой ступени, а теория автоматического управления — основой построения всей иерархической лестницы процессов управления, необходимых для комплексной автоматизации сложных объектов. В результате теорию автоматического управления можно рассматривать как обобщение и дальнейшее развитие теории автоматического регулирования, требующее, в частности, широкого использования понятия информации [50], которое в теории регулирования играет сравнительно небольшую роль.
Скачано с www.znanio.ru
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.