Открытый урок по алгебре и началам анализа в 11 классе. Тема: Обобщение и систематизация знаний по теме: «Свойства тригонометрических функций».

Открытый урок по алгебре и началам анализа в 11 классе.

Тема: Обобщение и систематизация знаний по теме: «Свойства тригонометрических функций».

Учитель: Стригина С.В.

Цели:

1)                  Обобщить и систематизировать знания по теме «Свойства тригонометрических функций».

2)                  Научить находить множество значений некоторых тригонометрических функцийвида    у= cos⁴x + sin⁴x  и y=acosx±bsinx .

3)                  Продолжить  работу по подготовке к ЕГЭ.

4)                  Продолжить работу по привитию интереса к предмету.

Задачи  урока:

1.  Образовательные:

- дать определения тригонометрическим функциям;

- рассмотреть основные  свойства тригонометрических функций;

- показать графики  тригонометрических функций.

2.  Развивающие:

- способствовать развитию   умений анализировать, устанавливать связи, причины и следствия;

- предвидеть возможные ошибки и способы их устранения;

- способствовать повышению концентрации внимания, развитию  памяти и речи.

3.  Воспитательные:

- способствовать развитию  интереса к предмету «Математика»;

- способствовать развитию самостоятельности мышления;

- в целях решения задач эстетического воспитания содействовать в ходе урока опрятному и грамотному построению графиков функций.

Методы обучения: словесные методы (рассказ, объяснение); наглядные методы (демонстрация, ТСО); практические методы.

Оборудование: компьютер, проектор, раздаточный материал.

План

1.      Мотивация.

2.      Фронтальный опрос.

3.      Решение задач на нахождение наименьшего и наибольшего значения функций.

4.      Групповые задания на построение графиков с помощью компьютера.

5.      Решение задач на нахождение множества значений функции.

6.      Самостоятельная работа.

7.      Решение заданий ЕГЭ. Подведение итога урока.

Ход урока.

I.    Мотивация: сообщение целей и плана работы.

II. Фронтальный опрос:

1)      Какова область определения и множество значений функций:

y=sinx,                    y=arcsinx,

у=cosx,                   y=arcosx,

у=tgx,                     y=arctgx,

у=ctgx,                  y=arcctgx.

2)      Найти наименьшее и наибольшее значение функций:

y=2sin²x,                   (Отв: 0 и 2).

y=cos²x-1,                     (Отв: -1 и 0).

y=3sinx+1,                    (Отв: -2 и 4).

у=sin²x-cos²x,               (Отв: -1 и 1).

,                (Отв: 0 и).

          (Отв:   и 0)

3)      Каков наименьший положительный период функций

y=2sin2x,                       (Отв: π).

y= -cos,                         (Отв: 4π).

                    (Отв: π /3).

III.             Решение задач.

1)Найти наименьшее инаибольшее значение функций:

а);

б)  ;

в) ;

г)  - самостоятельная работа №1.  

2) ,  найти все значения а, при которых данное уравнение имеет корни. Решить уравнение.

1)Найти наибольшее и наименьшее значение функций:

Показать решение примера.                       /учитель/

а)       

Преобразуем правую часть:

;

,

,

.

Ответ: наименьшее значение    наибольшее значение 1.

б) Решить:                                         /у доски – ученик/

.

Преобразуем правую часть:

,

,

Ответ: наименьшее значение ; наибольшее значение 1.

в) Найти Е(у), если                       /ученик/

I способ

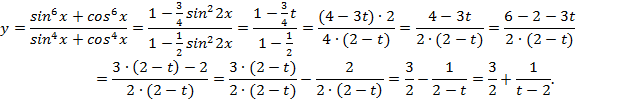
Еслиt=0, то   y=1;

еслиt=1, тоy=.

Ответ: []

II способ

.

Если t=sin²2x, где 0≤t≤1,  то подставив вместо t значенияt=0  и t=1 получим:

y(0)=1, y(1)= .

Ответ: наименьшее значение  , наибольшее 1.

г)  -          /самостоятельно/

Решение:

где t=sin²2x, 0≤t≤1,  то подставив вместо t значенияt=0  и t=1 получим:

y(0)=1, y(1)= 2.

Ответ: [1;2]

2) ,  найти все значения а, при которых данное уравнение имеет корни. Решить уравнение.            /ученик/

.

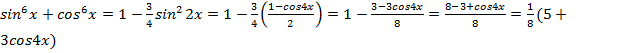Пусть, тогда

8a=5+3cos4x,

3cos4x=8a-5,

, так как   -1 ≤ cos 4x ≤ 1,  то

  /∙3,

-3≤8a-5≤3  /+5,

2≤8a≤8   /:8,

.

Решим уравнение:

.

;

Ответ:

IV.             Изобразить график функции  с помощью компьютера:       

а)                      /групповая работа/

б);                           

Описать алгоритм построения.

V.                № 397 (из учебника, автор  Алимов Ш.А.)

Найти наименьшее инаибольшее  значение функции

                    /ученик/

Пусть 3cos2x – 4 sin2x=a.

Разделим  обе части на 5, так как

;

Пусть 

            ,

,

-5≤а≤5.

Ответ: [-5;5].

VI.             Самостоятельная работа №2.

VII.          Решение заданий ЕГЭ.

Решить уравнения:

1)         .        /решает ученик/

Ответ:

2)                  /решает ученик/

Ответ: .

3)         .                     /работа в парах/

Ответ: .

VIII.        Подвести итог  урока.

IX.              Домашнее задание: №699, 774, 769,

Найти Е(у), если y=sin⁸x+cos⁸x