
Тема урока: «Сумма углов треугольника»
Класс: 7а
Дата: 25.02.2021
Цели:
Тип урока: изучение нового материала.
Оборудование: компьютер, презентация, карточки с заданиями, транспортир.
Я слышу – я забываю,
Я вижу – я запоминаю,
Я делаю – я успеваю.
Китайская мудрость.
ХОД УРОКА
Учитель приветствует учащихся, проверяется готовность к уроку.
2. Формулирование темы, цели и задачи урока.
Учитель. Американский математик, писатель Мартин Гарднер сказал: «Может показаться, что треугольник, столь тщательно изученный в древности, не таит в себе больше ничего неожиданного и необычного, связанного с треугольником. Действительно, например, в Атлантическом океане есть район, ограниченный линиями от Флориды к Бермудским островам, далее к Пуэрто-Рико и назад к Флориде через Багамы, который называют бермудским треугольником. Здесь часто зарождаются циклоны и штормы и, как говорят, иногда происходят необычные явления. Аналогичный «треугольник» в Тихом океане называют «дьявольским».
Ещё один удивительный треугольник называют невозможным. Он был открыт в 1934 году шведским художником Оскаром Реутерсвардом. Его легко нарисовать, но невозможно построить. 13- метровая скульптура невозможного треугольника из алюминия была воздвигнута в 1999 году в австралийском городе Перт (рис. 1-3).

Мы видим, что в действительности эта фигура треугольником не является и в одном из ракурсов кажется, что она имеет два прямых угла. А что вам известно о величинах углов треугольника? (Ожидаемый ответ. В треугольнике не может быть двух прямых углов).
Сегодня на уроке мы сформулируем и докажем свойство треугольника, которое нам поможет ответить на вопрос задачи: Чему равен угол B треугольника ABC (рис. 4).
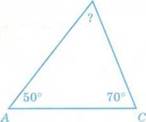
Рис. 4
Затем сообщается тема урока. Учащиеся с помощью учителя формулируют основную
цель урока.
3. Актуализация знаний
Выполнение устных упражнений
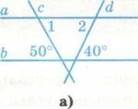
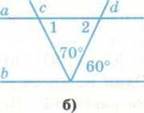
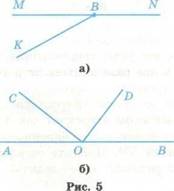 Есть ли на
рисунках пары смежных углов (рис. 5)? Назовите их.
Есть ли на
рисунках пары смежных углов (рис. 5)? Назовите их.
 |
 |
||
4. Усвоение новых знаний
1.Практическая работа
Для проведения практической работы учащиеся объединяются в три группы.
Каждая группа получает по два треугольника из цветной бумаги:
1-я группа — прямоугольный и равнобедренный,
2-я группа — остроугольный и равносторонний,
3-я группа — тупоугольный и прямоугольный равнобедренный.
Задание
Таблица
|
Виды треугольника |
Угол А |
Угол В |
Угол С |
|
По окончании работы представители групп записывают свои данные в сводную таблицу на доске.
- Посмотрите внимательно на данные последнего столбца таблицы. Что вы заметили? (Ожидаемый ответ. Все суммы близки к 180°.)
- Чем, по-вашему, объясняется небольшое различие в суммах углов треугольников? Тем, что нет никакой закономерности, или тем, что закономерность есть, но с помощью наших инструментов мы не можем установить её с достаточной точностью? (Учащиеся предполагают, что закономерность существует).
Учитель. Давайте убедимся в этом предположении. Для этого выполним следующее задание. У вас на столах два треугольника. Отрежьте углы одного из треугольников.
Теперь соедините их вместе так, чтобы вершины углов находились в одной точке, а сторона одного являлась стороной другого (рис. 7).

- Какой угол получим? (Ожидаемый ответ. Развернутый угол.)
- Выполните аналогичные действия для второго треугольника. Сделайте вывод о сумме углов треугольника.
2. Теорема о сумме углов треугольника
Учитель предлагает учащимся сформулировать теорему о сумме углов треугольника, организует деятельность по изучению теоремы в виде практической работы.
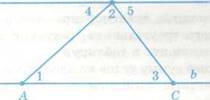 Рис.8
Рис.8
приведённое в учебнике, оформляют доказательство теоремы в тетрадях.
Учитель. А теперь ответьте на вопрос задачи (рис. 4): чему равен угол В треугольника ABC? (Ответ. 60°.)
5. Физкультминутка
Представьте, что вы - птица, ваши крылья крепко сжаты.
Соедините лопатки, напрягите спину так сильно, как только можете.
Вы ощущаете напряжение. Теперь медленно, не торопясь, расслабляйте свои мышцы.
Ваши крылья расправляются, становятся сильными, лёгкими, невесомыми. Вы ощущаете расслабление.
6. Применение новых знаний
Найдите неизвестный угол треугольника
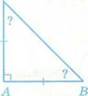
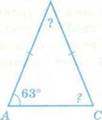
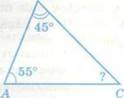
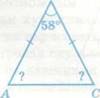
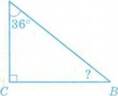
2. Письменные упражнения
1) Найдите все углы треугольника, если один из них в два раза меньше второго и на 20° больше третьего.
2) Найдите все углы треугольника, если их градусные меры относятся как 1:3:5.
3) Один из углов равнобедренного треугольника равен 50°. Найдите остальные углы. Сколько решений имеет задача?
3. Тест
Вариант 1
1) Могут ли два угла треугольника быть равными 108° и 82°?
а) Да; б) нет.
2) Один из острых углов прямоугольного треугольника равен 37°. Найдите второй острый угол.
а) 53°; б) 37°; в) 74°.
3) Один из углов равнобедренного треугольника равен 92°. Найдите остальные углы.
а) 88°, 88°; б) 44°, 44°; в) 88°, 44°.
Вариант 2
1) Могут ли два угла треугольника быть равными 98° и 82°?
а) Да; б) нет.
2) Один из острых углов прямоугольного треугольника равен 43°. Найдите второй острый угол.
а) 47°; б) 43°; в) 86°.
3) Один из углов равнобедренного треугольника равен 102°. Найдите остальные углы.
а) 78°, 78°; б) 39°, 78°; в) 39°, 39°.
7. Подведение итогов урока
Проверка результатов, обсуждение.
8. Рефлексия
Учащиеся по очереди продолжают предложения из числа представленных на экране.
1. Сегодня я узнал...
2. Меня заинтересовало...
3. Я научился...
4. Я смог...
5. Я приобрёл...
6. Я понял, что...
7. Мне надо поработать над...
8. Меня удивило...
9. Мне захотелось...
9. Домашнее задание
|
Уровень «3» |
Уровень «4» |
Уровень «5» |
|
№ 223 (а, б), № 227 (а) |
№ 223 (а, б), № 227 (а), № 228 (а) |
№ 223 (а, б), № 227 (а), № 228 (а), № 224 |
Проведите поиск
других доказательств теоремы (по желанию)
Учитель: Урок окончен, спасибо за работу!
Литература
1. Л.С.Атанасян. «Геометрия 7-9».
2. Е.М. Рабинович «Геометрия 7-9 . Задачи на готовых чертежах».
3. Программа по математике для общеобразовательных школ.
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.