Муниципальное общеобразовательное учреждение
«Школа-интернат для детей-сирот и детей, оставшихся без попечения родителей
«Семья» города Магнитогорска
Приложение № 4
К АООП ООО
Оценочные материалы
по математике
для 5, 7-9 классов
|
Составили: учителя математики Л.В.Маркина,Р.И.Аскарова |
Составитель:
учитель математики
Т.Л. Якименко
Контрольные работы даются на 1 административный час, в ходе которых проверяются следующие элементы содержания:
|
Код раздела |
Код контролируемого элемента |
Элементы содержания, проверяемые заданиями |
||
|
1 |
|
Числа и вычисления |
||
|
1.1 |
|
Натуральные числа |
||
|
1.1.1 |
Десятичная система счисления. Римская нумерация |
|||
|
1.1.2 |
Арифметические действия над натуральными числами |
|||
|
1.1.3 |
Степень с натуральным показателем |
|||
|
1.1.4 |
Делимость натуральных чисел. Простые и составные числа, разложение натурального числа на простые множители. |
|||
|
1.1.5 |
Признаки делимости на 2, 3, 5, 9, 10 |
|||
|
1.1.6 |
Наибольший общий делитель и наименьшее общее кратное |
|||
|
1.1.7 |
Деление с остатком |
|||
|
1.2 |
|
Дроби |
||
|
1.2.1 |
Обыкновенная дробь, основное свойство дроби. Сравнение дробей |
|||
|
1.2.2 |
Арифметические действия с обыкновенными дробями |
|||
|
1.2.3 |
Нахождение части от целого и целого по его части |
|||
|
1.2.4 |
Десятичная дробь, сравнение десятичных дробей |
|||
|
1.2.5 |
Арифметические действия с десятичными дробями |
|||
|
1.2.6 |
Представление десятичной дроби в виде обыкновенной дроби и обыкновенной в виде десятичной |
|||
|
1.3 |
|
Рациональные числа |
||
|
1.3.1 |
Целые числа |
|||
|
1.3.2 |
Модуль (абсолютная величина) числа |
|||
|
1.3.3 |
Сравнение рациональных чисел |
|||
|
1.3.4 |
Арифметические действия с рациональными числами |
|||
|
1.3.5 |
Степень с целым показателем |
|||
|
1.3.6 |
Числовые выражения, порядок действий в них, использование ск обок. Законы арифметических действий |
|||
|
1.4 |
|
Действительные числа |
||
|
1.4.1 |
Квадратный корень из числа |
|||
|
1.4.2 |
Корень третьей степени |
|||
|
1.4.3 |
Нахождение приближенного значения корня |
|||
|
1.4.4 |
Запись корней с помощью степени с дробным показателем |
|||
|
1.4.5 |
|
Понятие об иррациональном числе. Десятичные приближения иррациональных чисел. Действительные числа как бесконечные десятичные дроби |
||
|
1.4.6 |
Сравнение действительных чисел |
|||
|
1.5 |
|
Измерения, приближения, оценки |
||
|
|
1.5.1 |
Единицы измерения длины, площади, объёма, массы, времени, скорости |
||
|
1.5.2 |
Размеры объектов окружающего мира (от элементарных частиц до Вселенной), длительность процессов в окружающем мире |
|||
|
1.5.3 |
Представление зависимости между величинами в виде формул |
|||
|
1.5.4 |
Проценты. Нахождение процента от величины и величины по её проценту |
|||
|
1.5.5 |
Отношение, выражение отношения в процентах |
|||
|
1.5.6 |
Пропорция. Пропорциональная и обратно пропорциональная зависимости |
|||
|
1.5.7 |
Округление чисел. Прикидка и оценка результатов вычислений. Выделение множителя – степени десяти в записи числа. |
|||
|
2 |
|
Алгебраические выражения |
||
|
2.1 |
|
Буквенные выражения (выражения с переменными) |
||
|
2.1.1 |
Буквенные выражения. Числовое значение буквенного выражения Буквенные выражения. Числовое значение буквенного выражения |
|||
|
2.1.2 |
Буквенные выражения. Числовое значение буквенного выражения Допустимые значения переменных, входящих в алгебраические выражения |
|||
|
2.1.3 |
Подстановка выражений вместо переменных |
|||
|
2.1.4 |
Равенство буквенных выражений, тождество. Преобразования выражений |
|||
|
2.2 |
2.2.1 |
Свойства степени с целым показателем |
||
|
2.3 |
|
Многочлены |
||
|
2.3.1 |
Многочлен. Сложение, вычитание, умножение многочленов |
|||
|
2.3.2 |
Формулы сокращенного умножения: квадрат суммы и квадрат разности; формула разности квадратов |
|||
|
2.3.3 |
Разложение многочлена на множители |
|||
|
2.3.4 |
Квадратный трехчлен. Теорема Виета. Разложение квадратного трехчлена на линейные множители |
|||
|
2.3.5 |
Степень и корень многочлена с одной переменной |
|||
|
2.4 |
|
Алгебраическая дробь |
||
|
2.4.1 |
Алгебраическая дробь. Сокращение дробей |
|||
|
2.4.2 |
Действия с алгебраическими дробями |
|||
|
2.4.3 |
Рациональные выражения и их преобразования |
|||
|
2.5 |
2.5.1 |
Свойства квадратных корней и их применение в вычислениях |
||
|
3 |
|
Уравнения и неравенства |
||
|
3.1 |
|
Уравнения |
||
|
3.1.1 |
Уравнение с одной переменной, корень уравнения |
|||
|
3.1.2 |
Линейное уравнение |
|||
|
3.1.3 |
Квадратное уравнение, формула корней квадратного уравнения |
|||
|
3.1.4 |
Решение рациональных уравнений |
|||
|
3.1.5 |
Примеры решения уравнений высших степеней. Решение уравнений методом замены переменной. Решение уравнений методом разложения на множители
|
|||
|
|
|
|
||
|
3.1.6 |
Уравнение с двумя переменными; решение уравнения с двумя переменными |
|||
|
3.1.7 |
Система уравнений; решение системы |
|||
|
3.1.8 |
Система двух линейных уравнений с двумя переменными; решение подстановкой и алгебраическим сложением |
|||
|
|
3.1.9 |
Уравнение с несколькими переменными |
||
|
|
3.1.10 |
Решение простейших нелинейных систем |
||
|
3.2 |
|
Неравенства |
||
|
|
3.2.1 |
Числовые неравенства и их свойства |
||
|
|
3.2.2 |
Неравенство с одной переменной. Решение неравенства |
||
|
|
3.2.3 |
Линейные неравенства с одной переменной |
||
|
|
3.2.4 |
Системы линейных неравенств |
||
|
|
3.2.5 |
Квадратные неравенства |
||
|
3.3 |
|
Текстовые задачи |
||
|
|
3.3.1 |
Решение текстовых задач арифметическим способом |
||
|
|
3.3.2 |
Решение текстовых задач алгебраическим способом |
||
|
4 |
|
Числовые последовательности |
||
|
4.1 |
4.1.1 |
Понятие последовательности |
||
|
4.2 |
|
Арифметическая и геометрическая прогрессии |
||
|
|
4.2.1 |
Арифметическая прогрессия. Формула общего арифметической прогрессии |
||
|
|
4.2.2 |
Формула суммы первых нескольких членов арифметической прогрессии члена
|
||
|
|
4.2.3 |
Геометрическая прогрессия. Формула общего члена геометрической прогрессии
|
||
|
|
4.2.4 |
Формула суммы первых нескольких членов геометрической прогрессии |
||
|
|
4.2.5 |
Сложные проценты |
||
|
5 |
|
Функции |
||
|
5.1 |
|
Числовые функции |
||
|
|
5.1.1 |
Понятие функции. Область определения функции. Способы задания функции |
||
|
|
5.1.2 |
Примеры графических зависимостей, отражающих реальные процессы |
||
|
|
5.1.3 |
Линейная функция, её график, геометрический смысл коэффициентов |
||
|
|
5.1.4 |
График функции y=х |
||
|
|
5.1.5 |
График функции y=х3 |
||
|
|
5.1.6 |
График функции y=|x| |
||
|
|
5.1.7 |
Квадратичная функция, ее график. Парабола. Координаты вершины, ось симметрии |
||
|
|
5.1.8 |
Использование графиков функций для решения уравнений и систем |
||
|
6 |
|
Координаты на прямой и плоскости |
||
|
6.1 |
|
Координатная прямая |
||
|
|
6.1.1 |
Изображение чисел точками координатной прямой |
||
|
|
6.1.2 |
Геометрический смысл модуля |
||
|
6.2 |
|
Декартовы координаты на плоскости |
|
6.2.1 |
Декартовы координаты на плоскости; координаты точки |
|
|
6.2.2 |
Координаты середины отрезка |
|
|
6.2.3 |
Формула расстояния между двумя точками плоскости |
|
|
6.2.4 |
Уравнение прямой, угловой коэффициент прямой, условие параллельности прямых |
|
|
6.2.5 |
Уравнение окружности |
|
|
6.2.6 |
Графическая интерпретация уравнений с двумя переменными и их систем |
|
|
6.2.7 |
Графическая интерпретация неравенств с двумя переменными и их систем |
|
|
7 |
|
Геометрия |
|
7.1 |
|
Геометрические фигуры и их свойства. Измерение геометрических величин |
|
7.1.1 |
Начальные понятия геометрии |
|
|
7.1.2 |
Угол. Прямой угол. Острые и тупые углы. Вертикальные и смежные углы. Биссектриса угла и ее свойства
|
|
|
|
7.1.3 |
Прямая. Параллельность и перпендикулярность прямых |
|
7.1.4 |
Отрезок. Свойство серединного перпендикуляра к отрезку. Перпендикуляр и наклонная к прямой |
|
|
7.1.5 |
Понятие о геометрическом месте точек |
|
|
7.1.6 |
Преобразования плоскости. Движения. Симметрия |
|
|
7.2 |
|
Треугольник |
|
7.2.1 |
Высота, медиана, биссектриса, средняя линия треугольника; точки пересечения |
|
|
7.2.2 |
Равнобедренный и равносторонний треугольники. Свойства и признаки равнобедренного треугольника серединных перпендикуляров, биссектрис, медиан, высот или их продолжений |
|
|
7.2.3 |
Прямоугольный треугольник. Теорема Пифагора |
|
|
7.2.4 |
Признаки равенства треугольников |
|
|
7.2.5 |
Неравенство треугольника |
|
|
7.2.6 |
Сумма углов треугольника. Внешние углы треугольника |
|
|
7.2.7 |
Зависимость между величинами сторон и углов треугольника |
|
|
7.2.8 |
Теорема Фалеса |
|
|
7.2.9 |
Подобие треугольников, коэффициент подобия. Признаки подобия треугольников |
|
|
7.2.10 |
Синус, косинус, тангенс острого угла прямоугольного треугольника и углов от 00 до 1800. |
|
|
7.2.11 |
Решение прямоугольных треугольников. Теорема косинусов и теорема синусов. Основное тригонометрическое тождество. |
|
|
7.3 |
|
Многоугольники |
|
7.3.1 |
Параллелограмм, его свойства и признаки |
|
|
7.3.2 |
Прямоугольник, квадрат, ромб, их свойства и признаки |
|
|
7.3.3 |
Трапеция, средняя линия трапеции; равнобедренная трапеция |
|
|
7.3.4 |
Сумма углов выпуклого многоугольника |
|
|
7.3.5 |
Правильные многоугольники |
|
|
7.4 |
|
Окружность и круг |
|
7.4.1 |
Центральный, вписанный угол; величина вписанного угла |
|
|
7.4.2 |
Взаимное расположение прямой и окружности, двух окружностей |
|
|
|
7.4.3 |
Касательная и секущая к окружности; равенство отрезков касательных, проведённых из одной точки |
|
7.4.4 |
Окружность, вписанная в треугольник |
|
|
7.4.5 |
Окружность, описанная около треугольника |
|
|
7.4.6 |
Вписанные и описанные окружности правильного многоугольника |
|
|
7.5 |
|
Измерение геометрических величин |
|
7.5.1 |
Длина отрезка, длина ломаной, периметр многоугольника. Расстояние от точки до прямой |
|
|
7.5.2 |
Длина окружности |
|
|
7.5.3 |
Градусная мера угла, соответствие между величиной угла и длин ой дуги окружности |
|
|
7.5.4 |
Площадь и её свойства. Площадь прямоугольника |
|
|
7.5.5 |
Площадь параллелограмма |
|
|
7.5.6 |
Площадь трапеции |
|
|
7.5.7 |
Площадь треугольника |
|
|
7.5.8 |
Площадь круга, площадь сектора |
|
|
7.5.9 |
Формулы объёма прямоугольного параллелепипеда, куба, шара |
|
|
7.6 |
|
Векторы на плоскости |
|
|
7.6.1 |
Вектор, длина (модуль) вектора |
|
7.6.2 |
Равенство векторов |
|
|
7.6.3 |
Операции над векторами (сумма векторов, умножение вектора на число) |
|
|
7.6.4 |
Угол между векторами |
|
|
7.6.5 |
Коллинеарные векторы, разложение вектора по двум неколлинеарным векторам |
|
|
7.6.6 |
Координаты вектора |
|
|
7.6.7 |
Скалярное произведение векторов |
|
|
8 |
|
Статистика и теория вероятностей |
|
8.1 |
|
Описательная статистика |
|
8.1.1 |
Представление данных в виде таблиц, диаграмм, графиков |
|
|
8.1.2 |
Средние результатов измерений |
|
|
8.2 |
|
Вероятность |
|
8.2.1 |
Частота события, вероятность |
|
|
8.2.2 |
Равновозможные события и подсчёт их вероятности |
|
|
8.2.3 |
Представление о геометрической вероятности |
|
|
8.3 |
|
Комбинаторика |
|
|
8.3.1 |
Решение комбинаторных задач: перебор вариантов, комбинаторное правило умножения |
|
|
|
|
Критерии оценивания диагностической работы (для работы с итогом в 18 баллов)
Максимальный балл за выполнение работы составляет – 18 баллов. На основе баллов, выставленных за выполнение всех заданий работы, подсчитывается первичный балл, который переводится в отметку по пятибалльной шкале (таблица 1).
Таблица 1
Перевод баллов в отметку по пятибалльной шкале
|
% выполнения от максимального балла |
Количество баллов |
Цифровая отметка |
Уровневая шкала |
|
89-100 |
16-18 |
5 |
Повышенный |
|
72-88 |
13-15 |
4 |
|
|
56-71 |
10-12 |
3 |
Базовый |
|
Менее 56 |
Менее 10 |
2 |
Недостаточный |
Продолжительность работы
Продолжительность диагностической работы 45-60 минут.
Критерии оценивания самостоятельной работы (для работы с итогом в 9 баллов)
Максимальный балл за выполнение работы составляет – 9 баллов. На основе баллов, выставленных за выполнение всех заданий работы, подсчитывается первичный балл, который переводится в отметку по пятибалльной шкале (таблица 2).
Таблица 2
Перевод баллов в отметку по пятибалльной шкале
|
Процент выполнения от максимального балла |
Количество баллов |
Цифровая отметка |
Уровневая шкала |
|
98-100 |
8 - 9 |
5 |
Повышенный |
|
67-98 |
6 - 7 |
4 |
|
|
56-66 |
5-6 |
3 |
Базовый |
|
Менее 56 |
Менее 5 |
2 |
Недостаточный |
Продолжительность работы
Продолжительность диагностической работы 40-45 минут.
Алгебра 7 класс. Диагностическая работа (входная)
План диагностической работы
|
№ задания |
КЭС (код) |
Раздел программы (содержательная линия) |
Проверяемый планируемый результат |
Уровень сложности |
Тип задания |
Время выполнения (мин) |
Максимальный балл |
|
1 |
1.2.5 |
Числа и дроби |
Выполнять вычисления с рациональными числами, сочетая устные и письменные приёмы вычислений |
Базовый |
Со свободным, кратким однозначным ответом |
1 |
1 балл |
|
2 |
1.2.4 |
Числа и дроби |
Использовать понятия и умения, связанные с пропорциональностью величин, процентами в ходе решения математических задач |
Базовый |
Со свободным, кратким однозначным ответом |
3 |
1 балл |
|
3 |
1.2.5 |
Числа и дроби |
Выполнять вычисления с рациональными числами, сочетая устные и письменные приёмы вычислений |
Базовый |
Со свободным, кратким однозначным ответом |
2 |
1 балл |
|
4 |
3.1.1 |
Элементы алгебры |
Нахождение неизвестных компонентов арифметических действий. |
Базовый |
Со свободным, кратким однозначным ответом |
3 |
1 балл |
|
5 |
7.5.9 |
Геометрия |
Вычислять объём прямоугольного параллелепипеда. |
Базовый |
Со свободным, кратким однозначным ответом |
2 |
1 балл |
|
6 |
1.2.2 |
Числа и дроби |
Выполнять вычисления с рациональными числами, сочетая устные и письменные приёмы вычислений |
Базовый |
Со свободным, кратким однозначным ответом |
2 |
1 балл |
|
7 |
8.2.1 |
Статистика, вероятность, комбинаторика |
Понятие о случайном опыте и событии. Вычисление вероятности случайного события |
Базовый |
Со свободным, кратким однозначным ответом |
2 |
1 балл |
|
8 |
1.2.1 |
Измерения, приближения, оценка |
Использовать в ходе решения задач элементарные представления, связанные с приближёнными значениями величин. |
Базовый |
С выбором верного ответа из нескольких вариантов |
3 |
1 балл |
|
9 |
8.2.2 |
Статистика, вероятность, комбинаторика |
Решение комбинаторных задач перебором вариантов. |
Базовый |
Со свободным, кратким однозначным ответом |
2 |
1 балл |
|
10 |
6.1.1 |
Измерения, приближения, оценка |
Иллюстрация отношений между множествами с помощью диаграмм |
Базовый |
Со свободным, кратким однозначным ответом |
1 |
1 балл |
|
11 |
6.1.1 |
Геометрия |
Построение точки по её координатам, определение координат точки на плоскости. |
Повышенный |
С развернутым ответом |
4 |
2 балла |
|
12 |
6.1.3 |
Элементы алгебры |
Построение точки по её координатам, определение координат точки на плоскости. |
Повышенный |
С развернутым ответом |
4 |
2 балла |
|
13 |
1.5.3 |
Числа и дроби |
Использовать понятия и умения, связанные с пропорциональностью величин, процентами в ходе решения математических задач |
Повышенный |
С развернутым ответом |
7 |
2 балла |
|
14 |
3.1.1 |
Элементы алгебры |
Нахождение неизвестных компонентов арифметических действий. |
Повышенный |
С развернутым ответом |
4 |
2 балла |
|
|
|
|
|
|
|
40 мин |
18 баллов |
Вариант I
1 часть
В каждом задании первой части необходимо записать верный ответ, в отведенном для этого месте. Каждый верный ответ оценивается в один балл.
1.
Вычислите:
![]() ;
;
Ответ:______________________
2. Решите задачу: Челябинский Металлургический комбинат в 2008 году произвел 4,65 млн. тонн стали, что на 7% меньше, чем в 2007 году. Сколько млн. тонн стали было произведено в 2007 году? Ответ:____________________
3. Найдите значение
дроби: ![]() ;
;
Ответ:_______________________
4.
Решите
уравнение: ![]() ;
;
Ответ:_______________________
5. В прямоугольном параллелепипеде длина 6 см., ширина 4 см. Чему равна высота параллелепипеда, если его объем равен 120см3?
Ответ:_______________________
6.
Найдите
произведение: ![]()
Ответ:_______________________
7. В кармане лежат пять белых, 4 черных и 3 красных фишки. Наугад вытаскивают одну фишку. Какова вероятность, что достанут красную фишку?
Ответ:_______________________
8. Расставьте числа ![]() в порядке возрастания.
в порядке возрастания.
1) ![]()
2) ![]()
3) ![]()
Ответ:_______________________
9. Имеются три ручки, пять карандашей и два блокнота (все предметы разные). Сколькими способами можно составить набор, в который входит ручка, карандаш и блокнот?
Ответ:_______________________
10. На диаграмме показано количество жителей крупных городов Челябинской области (на 4 декабря 2017 года).

Найдите по диаграмме количество городов, число жителей которых превышает 100 тысяч.
Ответ:_______________________
II часть
Для записи решений и ответов каждого задания второй части используйте тетрадные листы в клетку. Запишите номер выполняемого задания, затем полное обоснованное решение и ответ. Каждое задание второй части оценивается от нуля до двух баллов.
11. На координатной плоскости постройте
отрезок ![]() , если
, если![]() .
.
12. Даны координаты точек ![]() В каких точках отрезок АВ пересекает
координатные прямые?
В каких точках отрезок АВ пересекает
координатные прямые?
13. Папа, мама и сын собирали грибы в
Каштакском бору. Папа и сын собрали ![]() от общей массы грибов, причем папа собрал
в два раза больше сына. Мама собрала 6 кг грибов. Сколько килограммов грибов
собрал сын?
от общей массы грибов, причем папа собрал
в два раза больше сына. Мама собрала 6 кг грибов. Сколько килограммов грибов
собрал сын?
14. Решите уравнение: ![]() ;
;
Вариант II
1часть
В каждом задании первой части необходимо записать верный ответ, в отведенном для этого месте. Каждый верный ответ оценивается в один балл.
1. Вычислите: ![]() ;
;
Ответ:_______________________
2. Решите задачу: Челябинский Металлургический комбинат в 2007 году произвел 5 млн. тонн стали, а в 2008 году 4,65 млн. тонн. На сколько процентов уменьшился выпуск продукции? Ответ:____________________
3.
Найдите
значение дроби: ![]() ;
;
Ответ:_______________________
4. Решите уравнение: ![]() ;
;
Ответ:_______________________
5. Объем прямоугольного параллелепипеда 120 см3. Чему равна высота параллелепипеда, если его длина 4 см., а ширина 3 см.?
Ответ:_______________________
6. Найдите
произведение: ![]() ;
;
Ответ:_______________________
7. В коробке лежат 7 красных, 5 желтых и 4 зеленых карандаша. Наугад вытаскивают один карандаш. Какова вероятность, что достали зеленый карандаш?
Ответ:_______________________
8.
Расставьте
числа![]() в порядке убывания.
в порядке убывания.
1)
![]()
2)
![]()
3)
![]()
Ответ:_______________________
9. Имеются 4 карандаша, 3 ластика и 2 альбома (все предметы различные). Сколькими способами можно составить набор, в который входит карандаш, ластик и альбом?
Ответ:_______________________
10. На диаграмме показано количество
жителей крупных городов Челябинской области (на 4 декабря 2017 года). 
Найдите по диаграмме количество городов, число жителей которых превышает 150 тысяч.
Ответ:_______________________
II часть
Для записи решений и ответов каждого задания второй части используйте тетрадные листы в клетку. Запишите номер выполняемого задания, затем полное обоснованное решение и ответ. Каждое задание второй части оценивается от нуля до двух баллов.
11. На координатной плоскости постройте
отрезок МК, если ![]() .
.
12. Даны координаты точек ![]() . В каких точках отрезок МК пересекает оси
координат?
. В каких точках отрезок МК пересекает оси
координат?
13. Папа, мама и сын собирали грибы в
Каштакском бору. Папа собрал ![]() , а мама
, а мама ![]() от общей массы грибов. Сколько
килограммов грибов собрала вся семья, если сын собрал 4 кг. Грибов?
от общей массы грибов. Сколько
килограммов грибов собрала вся семья, если сын собрал 4 кг. Грибов?
14. Решите уравнение: ![]() .
.
Планируемые результаты: Проверить уровень достижения результатов по основным темам курса математики 6 класса для обеспечения возможности успешного продолжения образования на базовом уровне.
Распределение заданий по разделам программ(ы)
|
№ п/п |
Раздел программы (содержательная линия) |
Количество заданий базового уровня сложности |
Количество заданий повышенного уровня сложности |
|
1. |
Числа и дроби |
4 |
1 |
|
2. |
Измерения, приближения, оценка |
2 |
|
|
3. |
Элементы алгебры |
1 |
2 |
|
4. |
Статистика, вероятность, комбинаторика |
2 |
|
|
5. |
геометрия |
1 |
1 |
|
|
Всего |
10 |
4 |
Инструкция по проверке и оценке работ
|
№ задания |
Планируемый результат |
Правильный ответ |
Критерии оценивания / Максимальный балл |
|
|
Вариант1 |
Вариант2 |
|||
|
1 |
Рациональный счет, устные вычисления |
3 |
3 |
1 балл |
|
2 |
Решение основных задач на процентное соотношение |
5 |
7 |
1 балл |
|
3 |
Выполнение действий с отрицательными числами |
-0,5 |
-0,25 |
1 балл |
|
4 |
Решение линейных уравнений |
4,75 |
8,5 |
1 балл |
|
5 |
Вычисление объема прямоугольного параллелепипеда |
5 |
10 |
1 балл |
|
6 |
Умножение обыкновенных дробей |
0,5 |
0,25 |
1 балл |
|
7 |
Применение классической формулы для вычисления вероятности случайного события |
0,25 |
0,25 |
1 балл |
|
8 |
Сравнение действительных чисел |
2 |
1 |
1 балл |
|
9 |
Решение простейших комбинаторных задач |
30 |
24 |
1 балл |
|
10 |
установление отношений между множествами с помощью диаграмм |
5 |
4 |
1 балл |
|
11 |
Задание системы координат и построение точек по данным координатам, построение отрезков. |
|
|
2 балла - отрезок построен правильно в заданной системе координат; 1 балл - отрезок построен правильно, содержаться неточности построения или задании системы координат 0 баллов другие случаи, не соответствующие указанным критериям |
|
12 |
Определение координат точек по построенному чертежу |
(-2;0); (0;4) |
(4;0); (0;2) |
2 балла получен верный обоснованный ответ,. 1 балл при верных рассуждениях допущена вычислительная ошибка, возможно приведшая к неверному ответу. 0 баллов другие случаи, не соответствующие указанным критериям |
|
13 |
Решение текстовых задач с помощью уравнения или по действиям |
4кг |
18кг |
2 балла получен верный обоснованный ответ. 1 балл при верных рассуждениях допущена вычислительная ошибка, возможно приведшая к неверному ответу. 0 баллов другие случаи, не соответствующие указанным критериям |
|
14 |
Понятие модуля числа, решение уравнения с модулем. |
|
|
2 балла правильно выполнены преобразования, получен верный ответ. 1 балл решение доведено до конца, но допущена ошибка вычислительного характера или описка, с ее учетом дальнейшие шаги выполнены верно. 0 баллов другие случаи, не соответствующие указанным критериям |
Контрольная работа № 1 «Выражения. Тождества»
План контрольной работы
|
№ задания |
КЭС (код) |
Раздел программы (содержательная линия) |
Проверяемый планируемый результат |
Уровень сложности |
Тип задания |
Время выполнения |
Максимальный балл |
|
1 |
2.1.4 |
Тождественные преобразования |
Выполнять несложные преобразования целых выражений: раскрывать скобки, приводить подобные слагаемые |
Базовый |
С кратким ответом |
3 мин |
1 балл |
|
2 |
2.1.3 |
Тождественные преобразования |
Выполнять несложные преобразования целых выражений: раскрывать скобки, приводить подобные слагаемые |
Базовый |
С кратким ответом |
3 мин |
1 балл |
|
3 |
3.1.1 |
Уравнения и неравенства |
Решать линейные уравнения |
Базовый |
С кратким ответом |
4 мин |
1 балл |
|
4 |
3.1.1 |
Уравнения и неравенства |
Решать линейные уравнения, выполнять простейшие исследования корней ур-я |
Базовый |
С кратким ответом |
4 мин |
1 балл |
|
5 |
3.1.1 |
Уравнения и неравенства |
Решать линейные уравнения с модулем |
Базовый |
С кратким ответом |
6 мин |
1 балл |
|
6 |
3.1.1 |
Текстовые задачи |
Решать задачи разных типов (на движение), связывающих три величины, выделять эти величины и отношения между ними |
Повышенный |
С развернутым ответом |
10 мин |
2 балла |
|
7 |
3.1.1 |
Уравнения и неравенства |
Решать линейные уравнения с параметром, исследовать корни уравнения |
Повышенный |
С развернутым ответом |
10 мин |
2 балла |
|
|
|
|
|
|
|
40 мин |
Общий балл |
Вариант I
1 часть
В каждом задании первой части необходимо записать верный ответ, в отведенном для этого месте. Каждый верный ответ оценивается в один балл.
1.
Запишите
многочлен ![]() в стандартном виде, в
ответ запишите степень многочлена.
в стандартном виде, в
ответ запишите степень многочлена.
Ответ:_______
2.
Чему
равно значение выражения ![]() если
если ![]() ?
?
Ответ:________
3.
Решите
уравнение: ![]()
Ответ:________
4.
При
каком значении параметра a,
число
4 является корнем уравнения ![]() ?
?
Ответ: ________
5.
Найдите
корень уравнения ![]() , если корней несколько,
в ответ запишите их сумму.
, если корней несколько,
в ответ запишите их сумму.
Ответ:________
II часть
Для записи решений и ответов каждого задания второй части используйте тетрадные листы в клетку. Запишите номер выполняемого задания, затем полное обоснованное решение и ответ. Каждое задание второй части оценивается от нуля до двух баллов.
6. Решите задачу: Катер по течению реки за 8 часов проплыл такое же расстояние, которое проплывает против течения реки за 12 часов. Во сколько раз собственная скорость катера больше скорости течения реки?
7.
При
каких целых значениях параметра a
уравнение ![]() имеет целые корни?
Найдите эти корни.
имеет целые корни?
Найдите эти корни.
Вариант II
1 часть
В каждом задании первой части необходимо записать верный ответ, в отведенном для этого месте. Каждый верный ответ оценивается в один балл.
1.
Запишите
многочлен ![]() в стандартном виде, в
ответ запишите степень многочлена.
в стандартном виде, в
ответ запишите степень многочлена.
Ответ:_______
2.
Чему
равно значение выражения ![]() если
если ![]() ?
?
Ответ: _______
3.
Решите
уравнение: ![]()
Ответ:_______
4.
При
каком значении параметра a,
число
3 является корнем уравнения ![]() ?
?
Ответ: _______
5.
Найдите
корень уравнения ![]() , если корней несколько,
в ответ запишите их сумму.
, если корней несколько,
в ответ запишите их сумму.
Ответ: _______
II часть
Для записи решений и ответов каждого задания второй части используйте тетрадные листы в клетку. Запишите номер выполняемого задания, затем полное обоснованное решение и ответ. Каждое задание второй части оценивается от нуля до двух баллов.
6. Решите задачу: Катер по течению реки за 8 часов проплыл такое же расстояние, которое проплывает против течения реки за 12 часов. Во сколько раз собственная скорость катера больше скорости течения реки?
7.
При
каких целых значениях параметра a
уравнение ![]() имеет целые корни?
Найдите эти корни.
имеет целые корни?
Найдите эти корни.
Инструкция по проверке и оценке работ
|
№ задания |
Планируемый результат |
Правильный ответ |
Критерии оценивания / Максимальный балл |
|
|
1 вариант |
2 вариант |
|||
|
1 |
Преобразование буквенных выражений: раскрытие скобок, приведение подобных, |
3 |
4 |
За верный ответ 1 балл |
|
2 |
Преобразование буквенных выражений: раскрытие скобок, приведение подобных, вычисление значения выражения при заданном значении переменной |
|
|
За верный ответ 1 балл |
|
3 |
Решение линейного уравнения |
|
8 |
За верный ответ 1 балл |
|
4 |
Решение линейного уравнения, исследование корней уравнения |
6 |
3 |
За верный ответ 1 балл |
|
5 |
Решение линейного уравнения с модулем |
3 |
5 |
За верный ответ 1 балл |
|
6 |
Решение текстовых задач с помощью уравнения |
В 5 раз |
В 5 раз |
2 балла получен верный обоснованный ответ. 1 балл при верных рассуждениях допущена вычислительная ошибка или описка, возможно приведшая к неверному ответу. 0 баллов другие случаи, не соответствующие указанным критериям |
|
7 |
Решение линейного уравнения с параметром, исследование корней уравнения |
при a=0, x=-1; при a=2, x=-3; при a=4, x=3; при a=6, x=1; |
при a=0, x=-1; при a=2, x=-3; при a=4, x=3; при a=6, x=1; |
2 балла получен верный обоснованный ответ. 1 балл при верных рассуждениях допущена вычислительная ошибка или описка, возможно приведшая к неверному ответу. 0 баллов другие случаи, не соответствующие указанным критериям |
|
|
|
|
Итого 9 |
|
Контрольная работа № 2 «Уравнения»
План контрольной работы
|
№ задания |
КЭС (код) |
Раздел программы (содержательная линия) |
Проверяемый планируемый результат |
Уровень сложности |
Тип задания |
Время выполнения |
Максимальный балл |
|
1 а) |
3.1.1 |
Уравнения |
Решать линейные уравнения |
Базовый |
С кратким ответом |
3 мин |
1 балл |
|
1 б) |
3.1.1 |
Уравнения |
Решать линейные уравнения |
Базовый |
С кратким ответом |
3 мин |
1 балл |
|
1 в) |
3.1.1 |
Уравнения |
Решать линейные уравнения |
Базовый |
С кратким ответом |
4 мин |
1 балл |
|
1 г) |
3.1.1 |
Уравнения |
Решать линейные уравнения |
Базовый |
С кратким ответом |
4 мин |
1 балл |
|
2 |
3.3.2 |
Текстовые задачи |
Решать задачи разных типов (на движение), связывающих три величины, выделять эти величины и отношения между ними |
Базовый |
С кратким ответом |
6 мин |
1 балл |
|
3 |
3.3.2 |
Текстовые задачи |
Решать задачи разных типов (на движение), связывающих три величины, выделять эти величины и отношения между ними |
Повышенный |
С развернутым ответом |
10 мин |
2 балла |
|
4 |
3.1.1 |
Уравнения |
Решать линейные уравнения |
Повышенный |
С развернутым ответом |
10 мин |
2 балла |
|
|
|
|
|
|
|
40 мин |
Общий балл |
Вариант I
1 часть
В каждом задании первой части необходимо записать верный ответ, в отведенном для этого месте. Каждый верный ответ оценивается в один балл.
1. Решите уравнение
а) 1/3 • х = 12;
Ответ: _______
б) 6 х – 10,2 = 0;
Ответ: _______
в) 5 х – 4,5 = 3 х + 2,5;
Ответ: _______
г) 2 х – (6 х – 5) = 45
Ответ: _______
2. Таня в школу сначала едет на автобусе, а потом идет пешком. Вся дорога у нее занимает 26 мин. Идет она на 6 мин дольше, чем едет на автобусе. Сколько минут она едет на автобусе?
Ответ: _______
II часть
Для записи решений и ответов каждого задания второй части используйте тетрадные листы в клетку. Запишите номер выполняемого задания, затем полное обоснованное решение и ответ. Каждое задание второй части оценивается от нуля до двух баллов.
3. В двух сараях сложено сено, причем в первом сарае сена в 3 раза больше, чем во втором. После того как из первого сарая увезли 20 т сена, а во второй привезли 10 т, в обоих сараях сена стало поровну. Сколько всего тонн сена было в двух сараях первоначально?
4. Решите уравнение
7 х – (х + 3) = 3• (2 х – 1)
Вариант II
1 часть
В каждом задании первой части необходимо записать верный ответ, в отведенном для этого месте. Каждый верный ответ оценивается в один балл.
1. Решите уравнение
а) 1/6 • х = 18;
Ответ: _______
б) 7 х + 11,9 = 0;
Ответ: _______
в) 6 х – 0,8 = 3 х + 2,2;
Ответ: _______
г) 5 х – (7 х + 7) = 9
Ответ: _______
2. Часть пути в 600 км турист пролетел на самолёте, а часть проехал на автобусе. На самолёте он проделал путь, в 9 раз больший, чем на автобусе. Сколько километров турист проехал на автобусе?
Ответ: _______
II часть
Для записи решений и ответов каждого задания второй части используйте тетрадные листы в клетку. Запишите номер выполняемого задания, затем полное обоснованное решение и ответ. Каждое задание второй части оценивается от нуля до двух баллов.
3. На одном участке было в 5 раз больше саженцев смородины, чем на другом. После того как с первого участка увезли 50 саженцев, а на второй посадили ещё 90, на обоих участках саженцев стало поровну. Сколько всего саженцев смородины было на двух участках первоначально?
4. Решите уравнение
6 х – (2х - 5) = 2• (2 х + 4)
Инструкция по проверке и оценке работ
|
№ задания |
Планируемый результат |
Правильный ответ |
Критерии оценивания / Максимальный балл |
|
|
1 вариант |
2 вариант |
|||
|
1 а) |
Решение линейного уравнения |
36 |
108 |
За верный ответ 1 балл |
|
1 б) |
Решение линейного уравнения |
1,7 |
- 1,7 |
За верный ответ 1 балл |
|
1 в) |
Решение линейного уравнения |
3,5 |
1 |
За верный ответ 1 балл |
|
1 г) |
Решение линейного уравнения. Раскрытие скобок. |
-10 |
-8 |
За верный ответ 1 балл |
|
2 |
Решение линейного уравнения с модулем |
10 мин |
60 км |
За верный ответ 1 балл |
|
3 |
Решение текстовых задач с помощью уравнения |
60 т |
210 саженцев |
2 балла получен верный обоснованный ответ. 1 балл при верных рассуждениях допущена вычислительная ошибка или описка, возможно приведшая к неверному ответу. 0 баллов другие случаи, не соответствующие указанным критериям |
|
4 |
Решение линейного уравнения. Раскрытие скобок |
х – любое число |
корней нет |
2 балла получен верный обоснованный ответ. 1 балл при верных рассуждениях допущена вычислительная ошибка или описка, возможно приведшая к неверному ответу. 0 баллов другие случаи, не соответствующие указанным критериям |
|
|
|
|
Итого 9 |
|
Контрольная работа № 3 «Функции»
План контрольной работы
|
№ задания |
КЭС (код) |
Раздел программы (содержательная линия) |
Проверяемый планируемый результат |
Уровень сложности |
Тип задания |
Время выполнения |
Максимальный балл |
|
1 |
5.1.1 |
Функции |
Умение находить значение функции по значению аргумента |
Базовый |
С кратким ответом |
3 мин |
1 балл |
|
2 |
5.1.1 |
Функции |
Умение находить абсциссу точки по заданной ординате |
Базовый |
С кратким ответом |
3 мин |
1 балл |
|
3 |
5.1.2 |
Функции |
Умение находить точку пересечения графика с коорд. осями |
Базовый |
С кратким ответом |
4 мин |
1 балл |
|
4 |
6.2.1 |
Функции |
Умение находить абсциссу точки по графику |
Базовый |
С выбором ответа |
3 мин |
1 балл |
|
5 |
5.1.1 |
Функции |
Умение задать уравнение прямой по двум точкам |
Базовый |
С кратким ответом |
5 мин |
1 балл |
|
6 |
5.1.2 |
Функции |
Умение построение кусочно-заданной функции, нахождение наибольшего и наименьшего значения функции |
Повышенный |
С развернутым ответом |
12 мин |
2 балла |
|
7 |
5.1.3 |
Функции |
Определять взаимное расположение графиков прямых, построение графика. |
Повышенный |
С развернутым ответом |
10 мин |
2 балла |
|
|
|
|
|
|
|
40 мин |
Общий балл |
Вариант I
1 часть
В каждом задании первой части необходимо записать верный ответ, в отведенном для этого месте. Каждый верный ответ оценивается в один балл.
1. Найдите
значение функции ![]() , если значение аргумента
равно 16.
, если значение аргумента
равно 16.
Ответ: _______
2. Определите,
при каком значении аргумента значение функции ![]() равно 2?
равно 2?
Ответ: _______
3. Прямая
![]() пересекает ось абсцисс в
точке
пересекает ось абсцисс в
точке ![]() . Найдите
. Найдите ![]() .
.
Ответ: ________
4. На графике указана высота Уральских гор, в зависимости от широты. Укажите широту, на которой высота Уральских гор наибольшая.
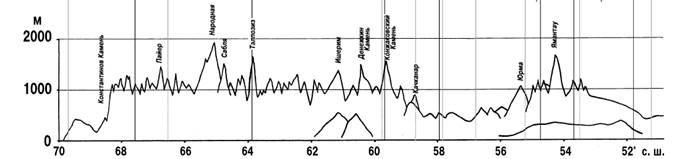
1)
Примерно
![]() ;
;
2)
Примерно
![]() северной широты;
северной широты;
3)
Примерно
![]() северной широты;
северной широты;
4)
Примерно
![]() северной широты;
северной широты;
Ответ:________
5. График
функции ![]() проходит через точки
проходит через точки ![]() . Вычислите значение
суммы
. Вычислите значение
суммы ![]() .
.
Ответ: ________
II часть
Для записи решений и ответов каждого задания второй части используйте тетрадные листы в клетку. Запишите номер выполняемого задания, затем полное обоснованное решение и ответ. Каждое задание второй части оценивается от нуля до двух баллов.
6. Постройте
график функции ![]() Какое наименьшее значение
может принимать эта функция?
Какое наименьшее значение
может принимать эта функция?
7. Прямая
![]() проходит через точку
проходит через точку ![]() и
параллельна прямой
и
параллельна прямой ![]() . Найдите коэффициенты k
и b, и постройте ее график.
. Найдите коэффициенты k
и b, и постройте ее график.
Вариант II
1 часть
В каждом задании первой части необходимо записать верный ответ, в отведенном для этого месте. Каждый верный ответ оценивается в один балл.
1.
Найдите
значение функции ![]() , если значение аргумента
равно 16.
, если значение аргумента
равно 16.
Ответ:________
2.
Определите,
при каком значении аргумента значение функции ![]() равно 2?
равно 2?
Ответ: ________
3. Прямая
![]() пересекает ось абсцисс в
точке
пересекает ось абсцисс в
точке ![]() . Найдите
. Найдите ![]() .
.
Ответ: ________
4. На графике указана высота Уральских гор, в зависимости от широты. Укажите широту, на которой высота Уральских гор наименьшая.
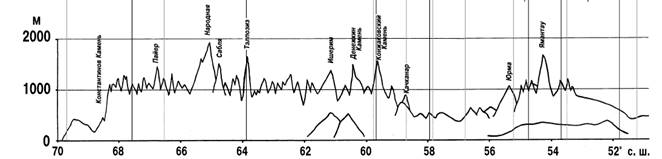
1) Примерно
![]() ;
;
2) Примерно
![]() северной широты;
северной широты;
3) Примерно
![]() северной широты;
северной широты;
4) Примерно
![]() северной широты;
северной широты;
Ответ: _________
5. График
функции ![]() проходит через точки
проходит через точки ![]() . Вычислите значение
суммы
. Вычислите значение
суммы ![]() .
.
Ответ: __________
II часть
Для записи решений и ответов каждого задания второй части используйте тетрадные листы в клетку. Запишите номер выполняемого задания, затем полное обоснованное решение и ответ. Каждое задание второй части оценивается от нуля до двух баллов.
6. Постройте
график функции ![]() Какое наименьшее
значение может принимать эта функция?
Какое наименьшее
значение может принимать эта функция?
7. Прямая
![]() проходит через точку
проходит через точку ![]() и
параллельна прямой
и
параллельна прямой ![]() . Найдите коэффициенты k
и b, и постройте ее график.
. Найдите коэффициенты k
и b, и постройте ее график.
Инструкция по проверке и оценке работ
|
№ задания |
Планируемый результат |
Правильный ответ |
Критерии оценивания / Максимальный балл |
|
|
1 вариант |
2 вариант |
|||
|
1 |
Нахождение значение функции по значению аргумента |
4 |
2 |
За верный ответ 1 балл |
|
2 |
Нахождение абсциссы точки по значению функции |
1,75 |
0,25 |
За верный ответ 1 балл |
|
3 |
Нахождение координат точки пересечения |
0,5 |
0,5 |
За верный ответ 1 балл |
|
4 |
Работа с графиком функции. Нахождение значение аргумента по значению функции. |
3 |
4 |
За верный ответ 1 балл |
|
5 |
Составление уравнения прямой по двум точкам |
3,5 |
2,5 |
За верный ответ 1 балл |
|
6 |
Построение графика кусочно-заданной функции, нахождение наименьшего значения функции по графику |
|
-1 |
2 балла получен верный обоснованный ответ. 1 балл при верных рассуждениях допущена вычислительная ошибка или описка, возможно приведшая к неверному ответу. 0 баллов другие случаи, не соответствующие указанным критериям |
|
7 |
Составление уравнения прямой, исследование взаимного расположения прямых. |
|
|
2 балла получен верный обоснованный ответ. 1 балл при верных рассуждениях допущена вычислительная ошибка или описка, возможно приведшая к неверному ответу. 0 баллов другие случаи, не соответствующие указанным критериям |
|
|
|
|
Итого 9 |
|
Контрольная работа № 4 «Степень с натуральным показателем»
План контрольной работы
|
№ задания |
КЭС (код) |
Раздел программы (содержательная линия) |
Проверяемый планируемый результат |
Уровень сложности |
Тип задания |
Время выполнения |
Максимальный балл |
|
1 |
2.2.1 |
Тождественные преобразования |
выполнять несложные преобразования выражений, содержащих степени с натуральным показателем |
Базовый |
С кратким ответом |
2 мин |
1 балл |
|
2 |
2.2.1 |
Числа |
выполнять несложные преобразования выражений, содержащих степени с натуральным показателем |
Базовый |
С кратким ответом |
3 мин |
1 балл |
|
3 |
2.2.1 |
Числа |
выполнять несложные преобразования для вычисления значений числовых выражений, содержащих степени с натуральным показателем |
Базовый |
С кратким ответом |
4 мин |
1 балл |
|
4 |
2.2.1 |
Числа |
Сравнивать числа, используя свойства степени и обыкновенной дроби |
Базовый |
с выбором ответа |
5 мин |
1 балл |
|
5 |
2.2.1 |
Уравнения и неравенства |
Решать уравнения, применяя свойства степени |
Базовый |
С кратким ответом |
6 мин |
1 балл |
|
6 |
2.2.1 |
Тождественные преобразования |
выполнять преобразования для вычисления значений числовых выражений, содержащих степени с натуральным показателем |
Повышенный |
С развернутым ответом |
10 мин |
2 балла |
|
7 |
3.3.1 |
Текстовые задачи |
Решать текстовые задачи с геометрическим содержанием, используя свойства объемов и свойства степеней |
Повышенный |
С развернутым ответом |
10 мин |
2 балла |
|
|
|
|
|
|
|
40 мин |
Общий балл |
Вариант I
1 часть
В каждом задании первой части необходимо записать верный ответ, в отведенном для этого месте. Каждый верный ответ оценивается в один балл.
1. Запишите
произведение ![]() в виде степени, в
ответе укажите показатель получившейся степени.
в виде степени, в
ответе укажите показатель получившейся степени.
Ответ: _______
2. Число
![]() представьте в виде куба.
Какое основание будет у получившейся степени?
представьте в виде куба.
Какое основание будет у получившейся степени?
Ответ: _______
3. Вычислите:
![]()
Ответ:________
4. Среди предложенных вариантов выберите тот, где числа расставлены в порядке возрастания:
1) ![]()
2) ![]()
3) ![]()
Ответ: ________
5.
Решите
уравнение: ![]() , если x
отрицательное число
, если x
отрицательное число
Ответ: ________
II часть
Для записи решений и ответов каждого задания второй части используйте тетрадные листы в клетку. Запишите номер выполняемого задания, затем полное обоснованное решение и ответ. Каждое задание второй части оценивается от нуля до двух баллов.
6. Вычислите:
![]()
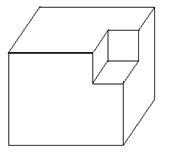
7. Из куба с ребром 8 вырезали куб с ребром 2 (см. рисунок). Найдите объем получившейся фигуры.

Вариант II
1 часть
В каждом задании первой части необходимо записать верный ответ, в отведенном для этого месте. Каждый верный ответ оценивается в один балл.
1. Запишите
произведение ![]() в виде степени, в
ответе укажите показатель получившейся степени.
в виде степени, в
ответе укажите показатель получившейся степени.
Ответ: ________
2. Число
![]() представьте в виде куба.
Какое основание будет у получившейся степени?
представьте в виде куба.
Какое основание будет у получившейся степени?
Ответ: ________
3. Вычислите:
![]()
Ответ:________
4. Среди предложенных вариантов выберите тот, где числа расставлены в порядке возрастания:
1) ![]()
2) ![]()
3) ![]()
Ответ: ________
5. Решите
уравнение: ![]() , если x
отрицательное число.
, если x
отрицательное число.
Ответ: ________
II часть
Для записи решений и ответов каждого задания второй части используйте тетрадные листы в клетку. Запишите номер выполняемого задания, затем полное обоснованное решение и ответ. Каждое задание второй части оценивается от нуля до двух баллов.
6. Вычислите:
![]()
7. Из куба с ребром 8 вырезали куб с ребром 2 (см. рисунок). Найдите объем получившейся фигуры.
Инструкция по проверке и оценке работ
|
№ задания |
Планируемый результат |
Правильный ответ |
Критерии оценивания / Максимальный балл |
|
|
1 вариант |
2 вариант |
|||
|
1 |
Применение понятия степень, для преобразования выражений |
9 |
8 |
За верный ответ 1 балл |
|
2 |
Применение свойств степени, для преобразования выражений |
4 |
9 |
За верный ответ 1 балл |
|
3 |
Применение свойств степени, для вычислений |
|
|
За верный ответ 1 балл |
|
4 |
Применение свойств степени для сравнения чисел |
2 |
2 |
За верный ответ 1 балл |
|
5 |
Решение уравнений, анализ полученных корней |
|
|
За верный ответ 1 балл |
|
6 |
Применение свойств степени, для вычислений, в более сложных случаях. |
1 |
1 |
2 балла получен верный обоснованный ответ. 1 балл при верных рассуждениях допущена вычислительная ошибка или описка, возможно приведшая к неверному ответу. 0 баллов другие случаи, не соответствующие указанным критериям |
|
7 |
Решение текстовой задачи, применяя свойства объемов и свойства степени |
504 |
504 |
2 балла получен верный обоснованный ответ. 1 балл при верных рассуждениях допущена вычислительная ошибка или описка, возможно приведшая к неверному ответу. 0 баллов другие случаи, не соответствующие указанным критериям |
|
|
|
|
Итого 9 |
|
Контрольная работа № 5 «Многочлены. Произведение одночлена на многочлен»
План контрольной работы
|
№ задания |
КЭС (код) |
Раздел программы (содержательная линия) |
Проверяемый планируемый результат |
Уровень сложности |
Тип задания |
Время выполнения |
Максимальный балл |
|
1 |
2.3.1 |
Тождественные преобразования |
Выполнять несложные преобразования для вычисления значений числовых выражений |
Базовый |
С кратким ответом |
2 мин |
1 балл |
|
2 |
2.1.3 |
Тождественные преобразования |
Выполнять несложные преобразования для вычисления значений числовых выражений |
Базовый |
С кратким ответом |
3 мин |
1 балл |
|
3 |
2.1.4 |
Тождественные преобразования |
Выполнять несложные преобразования целых выражений: раскрывать скобки, приводить подобные слагаемые; |
Базовый |
С кратким ответом |
4 мин |
1 балл |
|
4 |
2.1.4 |
Тождественные преобразования |
Выполнять несложные преобразования целых выражений |
Базовый |
С выбором ответа |
4 мин |
1 балл |
|
5 |
2.1.2 |
Тождественные преобразования |
Выполнять несложные преобразования целых выражений, оценивать наибольшее значение выражения |
Базовый |
С кратким ответом |
5 мин |
1 балл |
|
6 |
2.3.1 |
Тождественные преобразования |
Выполнять преобразования целых выражений: раскрывать скобки, приводить подобные слагаемые; доказывать тождества |
Повышенный |
С развернутым ответом |
12 мин |
2 балла |
|
7 |
3.1.1 |
Уравнения и неравенства |
Решать линейные уравнения с дробными коэффициентами |
Повышенный |
С развернутым ответом |
10 мин |
2 балла |
|
|
|
|
|
|
|
40 мин |
Общий балл |
Вариант I
1 часть
В каждом задании первой части необходимо записать верный ответ, в отведенном для этого месте. Каждый верный ответ оценивается в один балл.
1.
Приведите
многочлен к ![]() стандартному виду. В
ответ запишите степень полученного многочлена.
стандартному виду. В
ответ запишите степень полученного многочлена.
Ответ:_________
2.
Найдите
значение многочлена ![]()
![]() .
.
Ответ:__________
3. Упростите
выражение ![]()
Ответ:__________
4.
Из
данных многочленов выберите многочлен, тождественно равный выражению ![]() .
.
1) ![]() ;
;
2) ![]() ;
;
3) ![]() ;
;
4) ![]() ;
;
Ответ:__________
5.
Какое
наименьшее значение принимает выражение ![]() ;
;
Ответ:___________
II часть
Для записи решений и ответов каждого задания второй части используйте тетрадные листы в клетку. Запишите номер выполняемого задания, затем полное обоснованное решение и ответ. Каждое задание второй части оценивается от нуля до двух баллов.
6.
Докажите,
что если ![]() , то
, то
![]() .
.
7.
Решите
уравнение: ![]()
Вариант II
1 часть
В каждом задании первой части необходимо записать верный ответ, в отведенном для этого месте. Каждый верный ответ оценивается в один балл.
1.
Приведите
многочлен к ![]() стандартному виду. В
ответ запишите степень полученного многочлена.
стандартному виду. В
ответ запишите степень полученного многочлена.
Ответ:_________
2.
Найдите
значение многочлена ![]()
![]() .
.
Ответ:__________
3. Упростите
выражение ![]()
Ответ:__________
4.
Из
данных многочленов выберите многочлен, тождественно равный выражению ![]() .
.
1) ![]() ;
;
2) ![]() ;
;
3) ![]() ;
;
4) ![]() ;
;
Ответ:__________
5.
Какое
наибольшее значение принимает выражение ![]() ;
;
Ответ:___________
II часть
Для записи решений и ответов каждого задания второй части используйте тетрадные листы в клетку. Запишите номер выполняемого задания, затем полное обоснованное решение и ответ. Каждое задание второй части оценивается от нуля до двух баллов.
6.
Докажите,
что если ![]() , то
, то
![]() .
.
7.
Решите
уравнение: ![]()
Инструкция по проверке и оценке работ
|
№ задания |
Планируемый результат |
Правильный ответ |
Критерии оценивания / Максимальный балл |
|
|
1 вариант |
2 вариант |
|||
|
1 |
Владение понятием степени многочлена, преобразование выражений |
3 |
3 |
За верный ответ 1 балл |
|
2 |
Преобразование выражений, отыскание значений выражения при заданных значениях переменных |
|
|
За верный ответ 1 балл |
|
3 |
Преобразование рациональных выражений |
|
|
За верный ответ 1 балл |
|
4 |
Владение понятием тождественного выражения, преобразование выражений |
4 |
3 |
За верный ответ 1 балл |
|
5 |
Преобразование рациональных выражений и оценка его наибольшего значения |
|
6 |
За верный ответ 1 балл |
|
6 |
Доказательство тождества, используя преобразование целых рациональных выражений |
Тождество верно |
Тождество верно |
2 балла получен верный обоснованный ответ. 1 балл при верных рассуждениях допущена вычислительная ошибка или описка, возможно приведшая к неверному ответу. 0 баллов другие случаи, не соответствующие указанным критериям |
|
7 |
Решение уравнения, приводимого к линейному |
|
|
2 балла получен верный обоснованный ответ. 1 балл при верных рассуждениях допущена вычислительная ошибка или описка, возможно приведшая к неверному ответу. 0 баллов другие случаи, не соответствующие указанным критериям |
|
|
|
|
Итого 9 |
|
Контрольная работа № 6 «Произведение многочленов»
План контрольной работы
|
№ задания |
КЭС (код) |
Раздел программы (содержательная линия) |
Проверяемый планируемый результат |
Уровень сложности |
Тип задания |
Время выполнения |
Максимальный балл |
|
1 а) |
2.3.2 |
Числа |
Использовать формулы сокращенного умножения |
Базовый |
С кратким ответом |
3 мин |
1 балл |
|
1 б) |
2.1.4 |
Тождественные преобразования |
Выполнять несложные преобразования целых выражений: раскрывать скобки, приводить подобные слагаемые; |
Базовый |
С кратким ответом |
3 мин |
1 балл |
|
1 в) |
2.1.4 |
Тождественные преобразования |
Выполнять несложные преобразования целых выражений: раскрывать скобки, приводить подобные слагаемые; |
Базовый |
С кратким ответом |
4 мин |
1 балл |
|
1 г) |
2.1.4 |
Тождественные преобразования |
Выполнять несложные преобразования целых выражений: раскрывать скобки, приводить подобные слагаемые; |
Базовый |
С кратким ответом |
4 мин |
1 балл |
|
2 |
2.3.3 |
Тождественные преобразования |
Применять формулы сокращенного умножения для разложения на множители |
Базовый |
С кратким ответом |
6 мин |
1 балл |
|
3 |
2.3.1 |
Тождественные преобразования |
Выполнять преобразования целых выражений: раскрывать скобки, приводить подобные слагаемые |
Повышенный |
С развернутым ответом |
10 мин |
2 балла |
|
4 |
3.3.2 |
Текстовые задачи |
Решать текстовые задачи с геометрическим содержанием, используя формулы площади квадрата и прямоугольника |
Повышенный |
С развернутым ответом |
10 мин |
2 балла |
|
|
|
|
|
|
|
40 мин |
Общий балл |
Вариант I
1 часть
В каждом задании первой части необходимо записать верный ответ, в отведенном для этого месте. Каждый верный ответ оценивается в один балл.
1. Выполните умножение
а) (с + 2)(с – 3)
Ответ: _______
б) (2 а – 1)(3а + 4)
Ответ: _______
в) (5 х – 2 у)(4 х – у)
Ответ: _______
г) (а – 2 )( а2- 3 а + 6 )
Ответ: _______
2. Разложите на множители
а( а + 3 ) - 2( а + 3 )
Ответ: _______
II часть
Для записи решений и ответов каждого задания второй части используйте тетрадные листы в клетку. Запишите номер выполняемого задания, затем полное обоснованное решение и ответ. Каждое задание второй части оценивается от нуля до двух баллов.
3. Упростите выражение - 0,1 х( 2 х2+ 6 )( 5 – 4 х2).
4. Из прямоугольного листа фанеры вырезали квадратную пластинку, для чего с одной стороны листа фанеры отрезали полосу шириной 2 см, а с другой 3 см. Найдите сторону получившегося квадрата, если известно, что его площадь на 51 см2 меньше площади прямоугольника.
Вариант II
1 часть
В каждом задании первой части необходимо записать верный ответ, в отведенном для этого месте. Каждый верный ответ оценивается в один балл.
1. Выполните умножение
а) ( а – 5 )( а - 3 )
Ответ: _______
б) ( 5 х + 4 )( 2 х - 1 )
Ответ: _______
в) ( 3 p + 2 c )( 2 p + 4 c )
Ответ: _______
г) ( b – 2 )( b2+ 2 b - 3 )
Ответ: _______
2. Разложите на множители
х( х - у ) - а( х - у )
Ответ: _______
II часть
Для записи решений и ответов каждого задания второй части используйте тетрадные листы в клетку. Запишите номер выполняемого задания, затем полное обоснованное решение и ответ. Каждое задание второй части оценивается от нуля до двух баллов.
3. Упростите выражение 0,5 х( 4 х2- 1 )( 5 х2+ 2).
4. Бассейн имеет прямоугольную форму. Одна из его сторон на 6 м больше другой. Он окружён дорожкой, ширина которой 0,5 м. Найдите стороны бассейна, если площадь окружающей его дорожки 15 м2.
Инструкция по проверке и оценке работ
|
№ задания |
Планируемый результат |
Правильный ответ |
Критерии оценивания / Максимальный балл |
|
|
1 вариант |
2 вариант |
|||
|
1 а) |
Выполнение преобразований с использованием формул сокращенного умножения |
с2-с-6 |
а2-8а+15 |
За верный ответ 1 балл |
|
1 б) |
Выполнение несложных преобразований целых выражений: раскрытие скобок, приводить подобные слагаемые |
6а2+5а-4 |
10х2+3х-4 |
За верный ответ 1 балл |
|
1 в) |
Выполнение несложных преобразований целых выражений: раскрытие скобок, приводить подобные слагаемые |
20х2-13ху+2у2 |
6р2+16рс+8с2 |
За верный ответ 1 балл |
|
1 г) |
Выполнение несложных преобразований целых выражений: раскрытие скобок, приводить подобные слагаемые |
а3-5а2+12а-12 |
в3-7в+6 |
За верный ответ 1 балл |
|
2 |
Разложение на множители с использованием формул |
(а+3)(а-2) |
(х-у)(х+а) |
За верный ответ 1 балл |
|
3 |
Выполнение несложных преобразований целых выражений: раскрытие скобок, приводить подобные слагаемые |
0,8х5+1,4х3-3х |
10х5+1,5х3-х |
2 балла получен верный обоснованный ответ. 1 балл при верных рассуждениях допущена вычислительная ошибка или описка, возможно приведшая к неверному ответу. 0 баллов другие случаи, не соответствующие указанным критериям |
|
4 |
Решение текстовой задачи, применяя формулы площади квадрата и прямоугольника |
9 см |
4 м и 10 м |
2 балла получен верный обоснованный ответ. 1 балл при верных рассуждениях допущена вычислительная ошибка или описка, возможно приведшая к неверному ответу. 0 баллов другие случаи, не соответствующие указанным критериям |
|
|
|
|
Итого 9 |
|
Контрольная работа № 7 «Формулы сокращенного умножения»
План контрольной работы
|
№ задания |
КЭС (код) |
Раздел программы (содержательная линия) |
Проверяемый планируемый результат |
Уровень сложности |
Тип задания |
Время выполнения |
Максимальный балл |
|
1 |
2.3.2 |
Числа |
Использовать формулы сокращенного умножения для упрощения вычислений значений выражений; |
Базовый |
С кратким ответом |
3 мин |
1 балл |
|
2 |
2.3.2 |
Тождественные преобразования |
Применять формулы сокращенного умножения для преобразований |
Базовый |
С кратким ответом |
3 мин |
1 балл |
|
3 |
2.3.2 |
Числа |
Использовать формулы сокращенного умножения для упрощения вычислений значений выражений; |
Базовый |
С кратким ответом |
3 мин |
1 балл |
|
4 |
2.3.3 |
Тождественные преобразования |
Применять формулы сокращенного умножения для разложения на множители |
Базовый |
С выбором ответа |
7 мин |
1 балл |
|
5 |
2.3.2 |
Тождественные преобразования |
Применять формулы сокращенного умножения для преобразований |
Базовый |
С кратким ответом |
4 мин |
1 балл |
|
6 |
2.3.2 |
Тождественные преобразования |
Применять формулы сокращенного умножения для доказательства тождеств |
Повышенный |
С развернутым ответом |
10 мин |
2 балла |
|
7 |
2.3.2 |
Уравнения |
Применять формулы сокращенного умножения для преобразований |
Повышенный |
С развернутым ответом |
10 мин |
2 балла |
|
|
|
|
|
|
|
40 мин |
Общий балл |
Вариант I
1 часть
В каждом задании первой части необходимо записать верный ответ, в отведенном для этого месте. Каждый верный ответ оценивается в один балл.
1.
Используя
формулу квадрата суммы или разности, вычислите: ![]() .
.
Ответ:__________
2.
Найдите
значение выражения ![]() если
если ![]() .
.
Ответ:__________
3.
Вычислите:
![]() .
.
Ответ:__________
4.
Разложите
на множители выражение: ![]() .
.
1) ![]() ;
;
2) ![]() ;
;
3) ![]() ;
;
4) ![]() ;
;
Ответ:__________
5.
Найдите
значение выражения ![]() если
если ![]() .
.
Ответ:__________
II часть
Для записи решений и ответов каждого задания второй части используйте тетрадные листы в клетку. Запишите номер выполняемого задания, затем полное обоснованное решение и ответ. Каждое задание второй части оценивается от нуля до двух баллов.
6.
Докажите,
что при любом натуральном n
значение выражения ![]() делиться на 3.
делиться на 3.
7.
Решите
уравнение: ![]() .
.
Вариант II
1 часть
В каждом задании первой части необходимо записать верный ответ, в отведенном для этого месте. Каждый верный ответ оценивается в один балл.
1.
Используя
формулу квадрата суммы или разности, вычислите: ![]() .
.
Ответ:__________
2.
Найдите
значение выражения ![]() если
если ![]() .
.
Ответ:__________
3.
Вычислите:
![]() .
.
Ответ:__________
4.
Разложите
на множители выражение: ![]() .
.
1) ![]() ;
;
2) ![]() ;
;
3) ![]() ;
;
4) ![]() ;
;
Ответ:__________
5.
Найдите
значение выражения ![]() если
если ![]() .
.
Ответ:__________
II часть
Для записи решений и ответов каждого задания второй части используйте тетрадные листы в клетку. Запишите номер выполняемого задания, затем полное обоснованное решение и ответ. Каждое задание второй части оценивается от нуля до двух баллов.
6.
Докажите,
что при любом натуральном n
значение выражения ![]() делиться на 3.
делиться на 3.
7.
Решите
уравнение: ![]() .
.
Инструкция по проверке и оценке работ
|
№ задания |
Планируемый результат |
Правильный ответ |
Критерии оценивания / Максимальный балл |
|
|
1 вариант |
2 вариант |
|||
|
1 |
Выполнение вычислений с использованием формул сокращенного умножения |
|
|
За верный ответ 1 балл |
|
2 |
Выполнение преобразований с использованием формул сокращенного умножения |
4 |
9 |
За верный ответ 1 балл |
|
3 |
Выполнение вычислений с использованием формул сокращенного умножения |
0,2 |
1,2 |
За верный ответ 1 балл |
|
4 |
Разложение на множители с использованием формул |
2 |
3 |
За верный ответ 1 балл |
|
5 |
Преобразование выражений, отыскание значений выражения при заданных значениях переменных |
9 |
249 |
За верный ответ 1 балл |
|
6 |
Использование формул для доказательства тождеств |
Выражение делиться на 3 |
Выражение делиться на 3 |
2 балла получен верный обоснованный ответ. 1 балл при верных рассуждениях допущена вычислительная ошибка или описка, возможно приведшая к неверному ответу. 0 баллов другие случаи, не соответствующие указанным критериям |
|
7 |
Решение уравнений, методом разложения на множители |
|
|
2 балла получен верный обоснованный ответ. 1 балл при верных рассуждениях допущена вычислительная ошибка или описка, возможно приведшая к неверному ответу. 0 баллов другие случаи, не соответствующие указанным критериям |
|
|
|
|
Итого 9 |
|
Контрольная работа № 8 «Формулы сокращенного умножения»
План контрольной работы
|
№ задания |
КЭС (код) |
Раздел программы (содержательная линия) |
Проверяемый планируемый результат |
Уровень сложности |
Тип задания |
Время выполнения |
Максимальный балл |
|
1 а) |
2.3.1 |
Тождественные преобразования |
выполнять несложные преобразования целых выражений: раскрывать скобки, приводить подобные слагаемые |
Базовый |
С кратким ответом |
3 мин |
1 балл |
|
1 б) |
2.3.2 |
Тождественные преобразования |
выполнять несложные преобразования целых выражений: раскрывать скобки, приводить подобные слагаемые |
Базовый |
С кратким ответом |
3 мин |
1 балл |
|
1 в) |
2.3.2 |
Тождественные преобразования |
выполнять несложные преобразования целых выражений: раскрывать скобки, приводить подобные слагаемые |
Базовый |
С кратким ответом |
4 мин |
1 балл |
|
2 а) |
2.3.3 |
Тождественные преобразования |
Применять формулы сокращенного умножения для разложения на множители |
Базовый |
С кратким ответом |
4 мин |
1 балл |
|
2 б) |
2.3.3 |
Тождественные преобразования |
Применять формулы сокращенного умножения для разложения на множители |
Базовый |
С кратким ответом |
6 мин |
1 балл |
|
3 |
2.3.3 |
Тождественные преобразования |
Применять формулы сокращенного умножения для разложения на множители |
Повышенный |
С развернутым ответом |
10 мин |
2 балла |
|
4 |
2.1.2 |
Тождественные преобразования |
Доказывать тождества |
Повышенный |
С развернутым ответом |
10 мин |
2 балла |
|
|
|
|
|
|
|
40 мин |
Общий балл |
Вариант I
1 часть
В каждом задании первой части необходимо записать верный ответ, в отведенном для этого месте. Каждый верный ответ оценивается в один балл.
1. Упростите выражение:
а) (х - 3)(х – 7) – 2 х(3 х – 5);
Ответ: _______
б) 4 а( а - 2 ) – ( а – 4 )2;
Ответ: _______
в) 2( m + 1)2- 4 m
Ответ: _______
2. Разложите на множители:
а) х3 – 9 х;
Ответ: _______
б) -5 а2 – 10 ab – 5 b2.
Ответ: _______
II часть
Для записи решений и ответов каждого задания второй части используйте тетрадные листы в клетку. Запишите номер выполняемого задания, затем полное обоснованное решение и ответ. Каждое задание второй части оценивается от нуля до двух баллов.
3. Разложите на множители: 16 х4 – 81
4. Докажите, что выражение х2 – 4 х + 9 при любых значениях х принимает положительные значения.
Вариант II
1 часть
В каждом задании первой части необходимо записать верный ответ, в отведенном для этого месте. Каждый верный ответ оценивается в один балл.
1. Упростите выражение:
а) 2 х( х - 3 ) – 3 х( х + 5 );
Ответ: _______
б) ( а + 7 )( а - 1) + ( а – 3 )2;
Ответ: _______
в) 3( у + 5)2- 3 у2
Ответ: _______
2. Разложите на множители:
а) c3 – 16 c;
Ответ: _______
б) 3 а2 – 6 ab + 3 b2.
Ответ: _______
II часть
Для записи решений и ответов каждого задания второй части используйте тетрадные листы в клетку. Запишите номер выполняемого задания, затем полное обоснованное решение и ответ. Каждое задание второй части оценивается от нуля до двух баллов.
3. Разложите на множители: 81 а4 – 1
4. Докажите, что выражение - а2 + 4 а - 9 может принимать лишь отрицательные значения.
Инструкция по проверке и оценке работ
|
№ задания |
Планируемый результат |
Правильный ответ |
Критерии оценивания / Максимальный балл |
|
|
1 вариант |
2 вариант |
|||
|
1 а) |
Преобразование буквенных выражений: раскрытие скобок, приведение подобных |
-5х2+21 |
-х2-21х |
За верный ответ 1 балл |
|
1 б) |
Преобразование буквенных выражений: раскрытие скобок, приведение подобных, использование формулы квадрат разности |
3а2-16 |
2а2+2 |
За верный ответ 1 балл |
|
1 в) |
Преобразование буквенных выражений: раскрытие скобок, приведение подобных, использование формулы квадрат суммы |
2m2+2 |
30у+75 |
За верный ответ 1 балл |
|
2 а) |
Разложение на множители с использованием формул |
х(х-3)(х+3) |
с(с-4)(с+4) |
За верный ответ 1 балл |
|
2 б) |
Разложение на множители с использованием формул |
-5(а+в)2 |
3(а-в)2 |
За верный ответ 1 балл |
|
3 |
Разложение на множители с использованием формул |
(2х-3)(2х+3) (4х2+9) |
(3а-1)(3а+1) (9а2+1) |
2 балла получен верный обоснованный ответ. 1 балл при верных рассуждениях допущена вычислительная ошибка или описка, возможно приведшая к неверному ответу. 0 баллов другие случаи, не соответствующие указанным критериям |
|
4 |
Доказательство тождества |
Тождество верно |
Тождество верно |
2 балла получен верный обоснованный ответ. 1 балл при верных рассуждениях допущена вычислительная ошибка или описка, возможно приведшая к неверному ответу. 0 баллов другие случаи, не соответствующие указанным критериям |
|
|
|
|
Итого 9 |
|
Контрольная работа № 9 «Системы линейных уравнений»
План контрольной работы
|
№ задания |
КЭС (код) |
Раздел программы (содержательная линия) |
Проверяемый планируемый результат |
Уровень сложности |
Тип задания |
Время выполнения |
Максимальный балл |
|
1 |
3.1.6 |
Уравнения и неравенства |
Оперировать на базовом уровне понятиями: уравнение, корень уравнения, решение уравнения, проверять справедливость числовых равенств |
Базовый |
С кратким ответом |
3 мин |
1 балл |
|
2 |
3.1.7 |
Уравнения и неравенства |
Решать системы несложных линейных уравнений, |
Базовый |
С кратким ответом |
4 мин |
1 балл |
|
3 |
3.1.7 |
Текстовая задача |
Решать несложные текстовые задачи |
Базовый |
С кратким ответом |
5 мин |
1 балл |
|
4 |
5.1.3 |
Функция |
Составлять системы уравнений, используя условие прохождения прямой через точки |
Базовый |
С кратким ответом |
5 мин |
1 балл |
|
5 |
3.1.7 |
Уравнения и неравенства |
Решать системы уравнений опираясь на их геометрический смысл |
Базовый |
С кратким ответом |
3 мин |
1 балл |
|
6 |
3.1.7 |
Текстовая задача |
Решать текстовые задачи с помощью систем уравнений |
Повышенный |
С развернутым ответом |
10 мин |
2 балла |
|
7 |
3.1.7 |
Уравнения и неравенства |
Оценивать значение выражений, решать уравнение используя ограниченность выражений |
Повышенный |
С развернутым ответом |
10 мин |
2 балла |
|
|
|
|
|
|
|
40 мин |
Общий балл |
Вариант I
1 часть
В каждом задании первой части необходимо записать верный ответ, в отведенном для этого месте. Каждый верный ответ оценивается в один балл.
1. При
каком значении параметра b
пара чисел ![]() является решением
уравнения
является решением
уравнения ![]() ?
?
Ответ:________
2. Пара
чисел ![]() является решением
системы уравнений
является решением
системы уравнений ![]() . Найдите
. Найдите ![]() /
/
Ответ:_________
3. Решите задачу: Сумма двух чисел равна 140. Сумма 70% первого числа и 80% второго числа равна 104. Найдите эти числа. В ответ запишите большее из чисел.
Ответ:_________
4. График
линейной функции ![]() проходит через точки
проходит через точки ![]() , чему равен угловой
коэффициент данной прямой?
, чему равен угловой
коэффициент данной прямой?
Ответ:_________
5. При
каком значении параметра a
система ![]() имеет бесконечно много
решений?
имеет бесконечно много
решений?
Ответ:________
II часть
Для записи решений и ответов каждого задания второй части используйте тетрадные листы в клетку. Запишите номер выполняемого задания, затем полное обоснованное решение и ответ. Каждое задание второй части оценивается от нуля до двух баллов.
6. Решите задачу: Если между цифрами двузначного числа вписать это же двузначное число, то полученное четырехзначное число будет больше первоначального в 77 раз. Найдите данное число.
7. Решите
уравнение: ![]() .
.
Вариант II
1 часть
В каждом задании первой части необходимо записать верный ответ, в отведенном для этого месте. Каждый верный ответ оценивается в один балл.
1. При
каком значении параметра b
пара чисел ![]() является решением
уравнения
является решением
уравнения ![]() ?
?
Ответ:________
2. Пара
чисел ![]() является решением
системы уравнений
является решением
системы уравнений ![]() . Найдите
. Найдите ![]() /
/
Ответ:_________
3. Решите задачу: Разность первого и второго числа равна 30. Сумма 80% первого числа и 90% второго числа равна 177. Найдите эти числа. В ответ запишите большее из чисел.
Ответ:_________
4. График
линейной функции ![]() проходит через точки
проходит через точки ![]() , чему равен угловой
коэффициент данной прямой?
, чему равен угловой
коэффициент данной прямой?
Ответ:_________
5. При
каком значении параметра a
система ![]() имеет бесконечно много
решений?
имеет бесконечно много
решений?
Ответ:________
II часть
Для записи решений и ответов каждого задания второй части используйте тетрадные листы в клетку. Запишите номер выполняемого задания, затем полное обоснованное решение и ответ. Каждое задание второй части оценивается от нуля до двух баллов.
6. Решите задачу: Если между цифрами двузначного числа вписать это же двузначное число, то полученное четырехзначное число будет больше первоначального в 77 раз. Найдите данное число.
7. Решите
уравнение: ![]() .
.
Инструкция по проверке и оценке работ
|
№ задания |
Планируемый результат |
Правильный ответ |
Критерии оценивания / Максимальный балл |
|
|
1 вариант |
2 вариант |
|||
|
1 |
Умение применять понятия уравнения, решение уравнения. |
|
|
За верный ответ 1 балл |
|
2 |
Решение системы линейных уравнений |
|
|
За верный ответ 1 балл |
|
3 |
Решение текстовой задачи, составлением системы уравнений |
80 |
120 |
За верный ответ 1 балл |
|
4 |
Определение условия принадлежности точки графику функции. |
|
|
За верный ответ 1 балл |
|
5 |
Решение системы уравнений с помощью геометрического смысла. |
12 |
15 |
За верный ответ 1 балл |
|
6 |
Решение текстовой задачи, составлением системы уравнений |
15 |
15 |
2 балла получен верный обоснованный ответ. 1 балл при верных рассуждениях допущена вычислительная ошибка или описка, возможно приведшая к неверному ответу. 0 баллов другие случаи, не соответствующие указанным критериям |
|
7 |
Решить уравнение с двумя неизвестными, используя ограниченность выражений, составив систему уравнений. |
|
|
2 балла получен верный обоснованный ответ. 1 балл при верных рассуждениях допущена вычислительная ошибка или описка, возможно приведшая к неверному ответу. 0 баллов другие случаи, не соответствующие указанным критериям |
|
|
|
|
Итого 9 |
|
Диагностическая работа (итоговая работа 7 класс)
План диагностической работы
|
№ задания |
КЭС (код) |
Раздел программы (содержательная линия) |
Проверяемый планируемый результат |
Уровень сложности |
Тип задания |
Время выполнения (мин) |
Максимальный балл |
|
1 |
2.2.1 |
Тождественные преобразования |
Выполнять несложные преобразования для вычисления значений числовых выражений, содержащих степени с натуральным показателем |
Базовый |
Со свободным, кратким однозначным ответом |
1 |
1 балл |
|
2 |
2.2.1 |
Тождественные преобразования |
Выполнять несложные преобразования для вычисления значений числовых выражений, содержащих степени с натуральным показателем |
Базовый |
Со свободным, кратким однозначным ответом |
1 |
1 балл |
|
3 |
2.2.1 |
Числа и дроби |
Выполнять вычисления с рациональными числами, сочетая устные и письменные приёмы вычислений |
Базовый |
Со свободным, кратким однозначным ответом |
3 |
1 балл |
|
4 |
3.1.1 |
Уравнения и неравенства |
Решать линейные уравнения |
Базовый |
Со свободным, кратким однозначным ответом |
2 |
1 балл |
|
5 |
5.1.3 |
Функции |
По графику линейной функции определять знаки коэффициентов к и b |
Базовый |
С выбором верного ответа из нескольких вариантов |
1 |
1 балл |
|
6 |
3.1.1 |
Текстовые задачи |
Решать несложные сюжетные задачи разных типов на все арифметические действия |
Базовый |
Со свободным, кратким однозначным ответом |
3 |
1 балл |
|
7 |
2.3.2
|
Тождественные преобразования |
Выполнять несложные преобразования целых выражений: раскрывать скобки, приводить подобные слагаемые |
Базовый |
Со свободным, кратким однозначным ответом |
2 |
1 балл |
|
8 |
8.1.2 |
Статистика и теория вероятности |
Читать информацию, представленную в виде таблицы, определять основные статистические характеристики числовых наборов |
Базовый |
Со свободным, кратким однозначным ответом |
2 |
1 балл |
|
9 |
2.3.4 |
Тождественные преобразования |
Выполнять несложные преобразования целых выражений: раскладывать на множители способом группировки |
Базовый |
С выбором верного ответа из нескольких вариантов |
3 |
1 балл |
|
10 |
1.5.4 |
Статистика и теория вероятности |
Читать информацию, представленную в виде диаграммы |
Базовый |
Со свободным, кратким однозначным ответом |
3 |
1 балл |
|
11 |
5.1.1 |
Функции |
Находить значение аргумента по заданному значению функции в несложных ситуациях |
Базовый |
Со свободным, кратким однозначным ответом |
2 |
1 балл |
|
12 |
5.1.7 |
Уравнения и неравенства |
Решать системы несложных линейных уравнений алгебраически или графически |
Базовый |
Со свободным, кратким однозначным ответом |
2 |
1 балл |
|
13 |
2.3.3 |
Уравнения и неравенства |
Решать уравнения разложением на множители, используя вынесение общего множителя за скобку, формулы сокращенного умножения |
Повышенный |
С развернутым ответом |
4 |
2 балла 2 балла получен верный обоснованный ответ,. 1 балл при верных рассуждениях допущена вычислительная ошибка, возможно приведшая к неверному ответу. 0 баллов другие случаи, не соответствующие указанным критериям |
|
14 |
5.1.6 |
Функции |
Строить график линейной функции с модулем |
Повышенный |
С развернутым ответом |
6 |
2 балла 2 балла получен верный обоснованный ответ. 1 балл при верных рассуждениях допущена вычислительная ошибка, возможно приведшая к неверному ответу. 0 баллов другие случаи, не соответствующие указанным критериям |
|
15 |
1.5.3 |
Текстовые задачи |
Решать задачи разных типов (на работу, на движение), связывающих три величины, выделять эти величины и отношения между ними |
повышенный |
С развернутым ответом |
8 |
2 балла 2 балла получен верный обоснованный ответ. 1 балл при верных рассуждениях допущена вычислительная ошибка, возможно приведшая к неверному ответу. 0 баллов другие случаи, не соответствующие указанным критериям |
|
|
|
|
|
|
|
45 мин |
18 баллов |
Вариант I
1 часть
В каждом задании первой части необходимо записать верный ответ, в отведенном для этого месте. Каждый верный ответ оценивается в один балл.
1. Вычислите: ![]() ;
;
Ответ:________________________
2. Приведите одночлен
![]() к стандартному виду. В ответе укажите
степень полученного
одночлена.
к стандартному виду. В ответе укажите
степень полученного
одночлена.
Ответ:________________________
3. Значение какого из данных выражений является наименьшим?
1) ![]()
2) ![]() ;
;
3) ![]()
Ответ:________________________
4. Решите уравнение: ![]() ;
;
Ответ:________________________
5. На рисунке
изображен график линейной функции вида ![]() .
.

Определите знаки коэффициентов k и b.
1)
![]() ;
;
2)
![]() ;
;
3)
![]() ;
;
4)
![]() ;
;
Ответ:________________________
6. Решите задачу.
От Челябинска до Чебаркуля электричка движется на 6 минут дольше, чем от Чебаркуля до Златоуста. За сколько минут электричка дойдет от Челябинска до Чебаркуля, если весь путь от Челябинска до Златоуста (через Чебаркуль) занимает 3 часа 26 минут?
Ответ:________________________
7.
Найдите
значение выражения ![]() , при
, при ![]() .
.
Ответ:________________________
8. Результаты контрольной работы по математике в 7-а представлены в таблице:
|
Оценка |
«5» |
«4» |
«3» |
«2» |
|
Количество уч-ся. |
7 |
12 |
9 |
2 |
Найдите средний балл 7-а класса за эту контрольную работу.
Ответ:________________________
9. Разложите
многочлен ![]() на множители.
на множители.
1) ![]() ;
;
2) ![]() ;
;
3) ![]() ;
;
4) ![]() ;
;
Ответ:________________________
10. На диаграмме представлено распределение по природным зонам земель Челябинской области, общая площадь которой равна 88,3 тыс. км2.
Площадь какой природной зоны примерно равна 33 тыс. км2?
1) Лесостепная природная зона.
2) Степная природная зона.
3) Горнолесная природная зона.
4) Лесостепная или степная природные зоны.
Ответ:________________________
11. Функция задана формулой ![]() . При каком значении аргумента значение
функции равно 2?
. При каком значении аргумента значение
функции равно 2?
Ответ:________________________
12. Даны линейные функции ![]() и
и ![]() , которые
пересекаются в точке
, которые
пересекаются в точке ![]() . Найдите
. Найдите ![]() .
.
Ответ:________________________
II часть
Для записи решений и ответов каждого задания второй части используйте тетрадные листы в клетку. Запишите номер выполняемого задания, затем полное обоснованное решение и ответ. Каждое задание второй части оценивается от нуля до двух баллов.
13. Решите уравнение ![]() , разложив левую часть на множители.
, разложив левую часть на множители.
14. Постройте график функции ![]() .
.
15. Заказ по изготовлению деталей рабочий должен был выполнить за 20 дней. Но рабочий делал ежедневно по 2 детали сверх плана, а поэтому выполнил заказ за 18 дней. Сколько деталей сделал рабочий.
Вариант II
1 часть
В каждом задании первой части необходимо записать верный ответ, в отведенном для этого месте. Каждый верный ответ оценивается в один балл.
1.
Вычислите:
![]()
Ответ:________________________
2.
Приведите
одночлен ![]() к стандартному виду. В ответе укажите
степень полученного одночлена.
к стандартному виду. В ответе укажите
степень полученного одночлена.
Ответ:________________________
3. Значение какого из данных выражений является наименьшим?
1)
![]()
2)
![]() ;
;
3)
![]()
Ответ:________________________
4.
Решите
уравнение: ![]() ;
;
Ответ:________________________
5.
На
рисунке изображен график линейной функции вида ![]() .
.
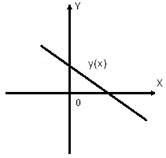
Определите знаки коэффициентов k и b.
1)
![]() ;
;
2)
![]() ;
;
3)
![]() ;
;
4)
![]() ;
;
Ответ:________________________
6. Решите задачу.
От Челябинска до Миасса электричка движется на 46 минут дольше, чем от Миасса до Златоуста. За сколько минут электричка дойдет от Челябинска до Миасса, если весь путь от Челябинска до Златоуста (через Миасс) занимает 3 часа 26 минут?
Ответ:________________________
7. Найдите значение
выражения ![]() при
при ![]() .
.
Ответ:________________________
8. Результаты контрольной работы по математике в 7-в представлены в таблице:
|
Оценка |
«5» |
«4» |
«3» |
«2» |
|
Количество уч-ся. |
8 |
12 |
9 |
1 |
Найдите средний балл 7-в класса за эту контрольную работу.
Ответ:________________________
9. Разложите
многочлен ![]() на множители.
на множители.
1) ![]() ;
;
2) ![]() ;
;
3) ![]() ;
;
4) ![]() ;
;
Ответ:________________________
10. На диаграмме представлено распределение по природным зонам земель Челябинской области.
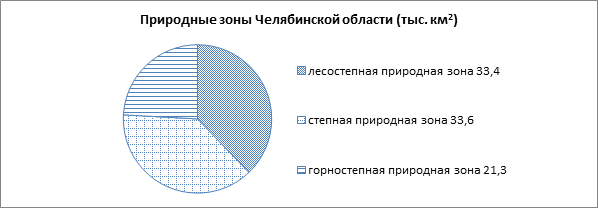
Площадь какой природной зоны составляет примерно равна 37% от общей площади земель Челябинской области?
1) Лесостепная природная зона.
2) Степная природная зона.
3) Горнолесная природная зона.
4) Лесостепная или степная природные зоны.
Ответ:________________________
11.
Функция
задана формулой ![]() . При каком значении аргумента значение
функции равно 2?
. При каком значении аргумента значение
функции равно 2?
Ответ:________________________
12.
Даны
линейные функции ![]() и
и ![]() , которые
пересекаются в точке
, которые
пересекаются в точке ![]() . Найдите
. Найдите ![]() .
.
Ответ:________________________
II часть
Для записи решений и ответов каждого задания второй части используйте тетрадные листы в клетку. Запишите номер выполняемого задания, затем полное обоснованное решение и ответ. Каждое задание второй части оценивается от нуля до двух баллов.
13.
Решите
уравнение ![]() , разложив левую часть на множители.
, разложив левую часть на множители.
14.
Постройте
график функции ![]() .
.
15.
Турист
рассчитал, что двигаясь с определенной скоростью, намеченный путь он пройдет за
2,5 часа. Но он увеличил скорость на ![]() , поэтому прошел путь за 2 часа. Найдите
длину пути.
, поэтому прошел путь за 2 часа. Найдите
длину пути.
Распределение заданий по разделам программ(ы)
|
№ п/п |
Раздел программы (содержательная линия) |
Количество заданий базового уровня сложности |
Количество заданий повышенного уровня сложности |
|
1. |
Числа и дроби |
1 |
|
|
2. |
Тождественные преобразования |
4 |
|
|
3. |
Уравнения и неравенства |
2 |
1 |
|
4. |
Статистика и теория вероятности |
2 |
|
|
5. |
Функции |
2 |
1 |
|
6. |
Текстовые задачи |
1 |
1 |
|
|
Всего |
12 |
3 |
Инструкция по проверке и оценке работ
|
№ задания |
Планируемый результат |
Правильный ответ |
Критерии оценивания / Максимальный балл |
||
|
Вариант1 |
Вариант2 |
||||
|
1 |
Рациональный счет, свойства степени |
|
|
1 балл |
|
|
2 |
Свойства степени, стандартный вид одночлена |
8 |
9 |
1 балл |
|
|
3 |
Рациональный счет, формулы сокращенного умножения |
2 |
3 |
1 балл |
|
|
4 |
Решение линейных уравнений |
0,5 |
2 |
1 балл |
|
|
5 |
График линейной функции, свойства линейной функции |
4 |
3 |
1 балл |
|
|
6 |
Решение текстовых задач с помощью уравнения или по действиям |
100 |
126 |
1 балл |
|
|
7 |
Преобразование буквенных выражений: раскрытие скобок, приведение подобных, вычисление значения выражения при заданном значении переменной |
2 |
12 |
1 балл |
|
|
8 |
Чтение информации, представленной в виде таблицы, определение основных статистических характеристик числовых наборов |
3,8 |
3,9 |
1 балл |
|
|
9 |
Разложение многочлена на множители |
4 |
2 |
1 балл |
|
|
10 |
установление отношений между множествами с помощью диаграмм |
1 |
1 |
1 балл |
|
|
11 |
Вычисление значения аргумента по заданному значению функции |
6 |
3 |
1 балл |
|
|
12 |
Определение координат точки пересечения прямых по построенному чертежу или решением системы уравнений |
6 |
5 |
1 балл |
|
|
13 |
Разложение многочлена на множители, решение уравнений старших степеней |
|
|
2 балла правильно выполнены преобразования, получен верный ответ. 1 балл решение доведено до конца, но допущена ошибка вычислительного характера или описка, с ее учетом дальнейшие шаги выполнены верно. 0 баллов другие случаи, не соответствующие указанным критериям |
|
|
14 |
Построение графика линейной функции с модулем |
См. рисунок |
См. рисунок |
2 балла верно и обоснованно построен график. 1 балл при верных рассуждениях допущена вычислительная ошибка, или описка, возможно приведшая к неверному ответу. 0 баллов другие случаи, не соответствующие указанным критериям |
|
|
15 |
Решение текстовых задач с помощью уравнения |
360 деталей |
10 км |
2 балла получен верный обоснованный ответ. 1 балл при верных рассуждениях допущена вычислительная ошибка, возможно приведшая к неверному ответу. 0 баллов другие случаи, не соответствующие указанным критериям |
|
Ответ к заданию 14 (построение графика)
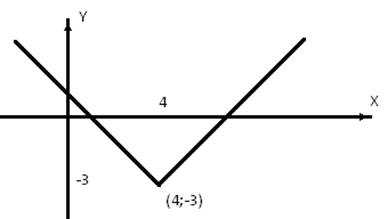
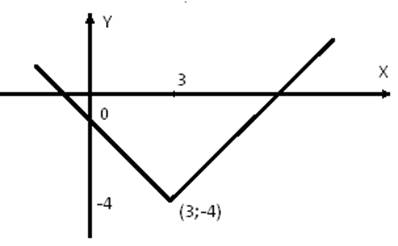
Геометрия 7 класс. Контрольная работа № 1 «Начальные геометрические сведения»
План контрольной работы
|
№ задания |
КЭС (код) |
Раздел программы (содержательная линия) |
Проверяемый планируемый результат |
Уровень сложности |
Тип задания |
Время выполнения (мин) |
Максимальный балл |
|
1 |
7.1.1 |
Геометрические фигуры. Прямая и отрезок.
|
Оперировать на базовом уровне понятиями: равенство фигур, равные фигуры. оперировать представлениями о длине, площади, объеме как величинами |
Базовый |
Со свободным, кратким однозначным ответом |
5 |
1 балл |
|
2 |
7.1.2 |
Измерения и вычисления. Измерение углов
|
Свободно оперировать понятиями длина, величина угла как величинами. |
Базовый |
Со свободным, кратким однозначным ответом |
5 |
1 балл |
|
3 |
7.1.2 |
Геометрические фигуры. Смежные и вертикальные углы |
Оперировать на базовом уровне понятиями: смежные и вертикальные углы |
Базовый |
Со свободным, кратким однозначным ответом |
5 |
1 балл |
|
4 |
7.1.2 |
Измерения и вычисления. Смежные и вертикальные углы |
Решать задачи на нахождение геометрических величин по образцам или алгоритмам. |
Базовый |
Со свободным, кратким ответом |
5 |
1 балл |
|
5 |
7.1.2 |
Измерения и вычисления. Смежные и вертикальные углы |
Решать задачи на нахождение геометрических величин по образцам или алгоритмам |
Базовый |
Со свободным, кратким однозначным ответом |
5 |
1 балл |
|
6 |
7.1.2 |
Измерения и вычисления. Смежные и вертикальные углы. Биссектриса угла |
Геометрические факты для решения задач, в том числе, предполагающих несколько шагов решения |
Повышенный |
С развернутым ответом |
7 |
2 балла |
|
7 |
7.1.4 |
Измерения и вычисления. Вычисление отрезков
|
Геометрические факты для решения задач, в том числе, предполагающих несколько шагов решения |
Повышенный |
С развернутым ответом |
8 |
2 балла |
|
|
|
|
|
|
|
40 мин |
9 баллов |
Вариант I
1 часть
В каждом задании первой части необходимо записать верный ответ, в отведенном для этого месте. Каждый верный ответ оценивается в один балл.
1. На отрезке PK отмечена точка М. Известно, что РМ в два раза больше МК. Найдите длину отрезка РМ, если РК=180 см. Ответ выразите в метрах.
Ответ:______________________
2. Луч ОС проходит между сторонами угла АОВ. Известно, что угол АОС равен 570, а угол АОВ равен 1120. Найдите градусную меру угла СОВ.
Ответ:______________________
![]()
3. Прямые АС и BD пересекаются в точке К. Какие утверждения являются верными?
1) Углы АКВ и DКС – смежные
2) Углы АКВ и DКС – вертикальные
3) Углы АКВ и ВКС – смежные
4) Углы АКВ и ВКС – вертикальные
Ответ:______________________
4. Один из смежных углов в 4 раз больше другого. Найдите величины этих углов.
Ответ:______________________
5. Сумма двух вертикальных углов, образованных при пересечении прямых aи cравна 2500. Найдите величину меньшего из углов, образованных этими прямыми.
Ответ:______________________
II часть
Для записи решений и ответов каждого задания второй части используйте тетрадные листы в клетку. Запишите номер выполняемого задания, затем полное обоснованное решение и ответ. Каждое задание второй части оценивается от нуля до двух баллов.
6. Даны смежные углы АОВ и ВОС. ОК – биссектриса угла АОВ. Найдите угол ВОК, если величина угла ВОС равна 1500.
7. Семиклассники одной из школ города Златоуста провели воскресный день в Национальном парке «Таганай». Вечером Максим предложил папе решить задачу: «Сосна (С), ель (Е) и береза (В) расположены на одной прямой. Известно, что СЕ : ВЕ = 5 : 3. Каким может быть расстояние между елью (Е) и березой (В), если расстояние между сосной (С) и березой (В) равно 16 м?»
Вариант II
1 часть
В каждом задании первой части необходимо записать верный ответ, в отведенном для этого месте. Каждый верный ответ оценивается в один балл.
1. На отрезке PK отмечена точка М. Известно, что РМ в три раза меньше МК. Найдите длину отрезка РМ, если РК=560 см. Ответ выразите в метрах.
Ответ:______________________
2. Луч ОМ проходит между сторонами угла АОВ. Известно, что угол АОМ равен 630, а угол АОВ равен 1180. Найдите градусную меру угла МОВ.
Ответ:______________________
3.
![]() Прямые АВ и СDпересекаются
в точке М. Какие утверждения являются верными?
Прямые АВ и СDпересекаются
в точке М. Какие утверждения являются верными?
1) Углы АМDи ВМС – смежные
2) Углы АМС и ВМD – вертикальные
3) Углы АМС и ВМС – смежные
4) Углы АМDи ВМD– вертикальные
Ответ:______________________
4. Один из смежных углов на 360 больше другого. Найдите величины этих углов.
Ответ:______________________
5. Сумма двух вертикальных углов, образованных при пересечении прямых aи cравна 700. Найдите величину большего из углов, образованных этими прямыми.
Ответ:______________________
II часть
Для записи решений и ответов каждого задания второй части используйте тетрадные листы в клетку. Запишите номер выполняемого задания, затем полное обоснованное решение и ответ. Каждое задание второй части оценивается от нуля до двух баллов.
6. Даны смежные углы АОВ и ВОС. ОМ– биссектриса угла АОВ. Найдите величину угла АОМ, если величина угла ВОС равна 800.
7. Семиклассники одной из школ города Златоуста провели воскресный день в Национальном парке «Таганай». В понедельник на уроке геометрии Маша предложила одноклассникам решить задачу: «Сосна (С), ель (Е) и береза (В) расположены на одной прямой. Известно, что СЕ : ВЕ=4 : 7. Каким может быть расстояние между елью (Е) и березой (В), если расстояние между сосной (С) и березой (В) равно 33 м?»
Инструкция по проверке и оценке работ
|
№ задания |
Планируемый результат |
Правильный ответ |
Критерии оценивания / Максимальный балл |
|
|
Вариант1 |
Вариант2 |
|||
|
1 |
Решение задачи на свойства длин отрезков |
1,2 |
1,4 |
1 балл |
|
2 |
Решение задач на свойства смежных и вертикальных углов |
550 |
550 |
1 балл |
|
3 |
Анализ геометрических высказываний. |
23 |
23 |
1 балл |
|
4 |
Решение задач на свойства смежных и вертикальных углов |
1440, 360 |
720, 1080 |
1 балл |
|
5 |
Решение задач на свойства смежных и вертикальных углов |
550 |
1450 |
1 балл |
|
6 |
Решение задачи на применение свойств смежных углов и биссектрисы |
150 |
500 |
2 балла - ход решения верный, все его шаги выполнены правильно, получен верный ответ 1 балл - ход решения верный, все его шаги выполнены правильно, но даны неполные объяснения или допущена одна вычислительная ошибка |
|
7 |
Решение задачи на нахождение длин отрезков |
6 м |
21 м |
2 балла - ход решения верный, все его шаги выполнены правильно, получен верный ответ 1 балл - ход решения верный, все его шаги выполнены правильно, но даны неполные объяснения или допущена одна вычислительная ошибка |
Контрольная работа № 2 «Треугольники»
План контрольной работы
|
№ задания |
КЭС (код) |
Раздел программы (содержательная линия) |
Проверяемый планируемый результат |
Уровень сложности |
Тип задания |
Время выполнения(мин) |
Максимальный балл |
|
1 |
7.2.4 |
Отношения. Признаки равенства треугольников
|
Оперировать на базовом уровне понятиями: равенство фигур, равные фигуры. |
Базовый |
Со свободным, кратким однозначным ответом |
5 |
1 балл |
|
2 |
7.2.2 |
Измерения и вычисления. Равнобедренный треугольник
|
Свободно оперировать понятиями длина, величина угла как величинами. |
Базовый |
Со свободным, кратким однозначным ответом |
5 |
1 балл |
|
3 |
7.2.2 |
Отношения. Признаки равнобедренного треугольника |
Решать задачи на применение признаков |
Базовый |
Со свободным, кратким однозначным ответом |
5 |
1 балл |
|
4 |
7.2.2 |
Отношения. Признаки равенства треугольников |
Оперировать на базовом уровне понятиями: равенство фигур, равные фигуры. |
Базовый |
Со свободным, кратким однозначным ответом |
5 |
1 балл |
|
5 |
7.2.2 |
Построения геометрических объектов |
Изображать геометрические объекты по их свойствам |
Базовый |
Со свободным, кратким однозначным ответом |
5 |
1 балл |
|
6 |
7.2.4 |
Отношения. Признаки равенства треугольников |
Геометрические факты для решения задач, в том числе, предполагающих несколько шагов решения |
Повышенный |
С развернутым ответом |
7 |
2 балла |
|
7 |
7.2.4 |
Отношения. Признаки равенства треугольников. Свойства окружности
|
Геометрические факты для решения задач, в том числе, предполагающих несколько шагов решения |
Повышенный |
С развернутым ответом |
8 |
2 балла |
|
|
|
|
|
|
|
40 мин |
9 баллов |
Вариант I
1 часть
В каждом задании первой части необходимо записать верный ответ, в отведенном для этого месте. Каждый верный ответ оценивается в один балл.
1.
![]() На
рисунке изображены равные треугольники АВС и МРК. Используя
данные рисунка, укажите верное равенство.
На
рисунке изображены равные треугольники АВС и МРК. Используя
данные рисунка, укажите верное равенство.
1)Величина угла К равна 500
2)Величина угла Р равна 500
3)Величина угла М равна 500
Ответ:______________________
2. В равнобедренном треугольнике АВС АВ=ВС. Периметр треугольника равен 18 см. Найдите боковую сторону треугольника, если его основание равно 4,6 см.
Ответ:______________________
3. Периметр треугольника АСЕ равен 77 см. Сторона АС в 3 раза больше стороны АЕ, углы А и Е равны. Найдите длины сторон треугольника АСЕ.
Ответ:______________________
4.
![]() Биссектриса CK
угла АСЕ перпендикулярна отрезку АЕ. Найдите градусную меру угла САЕ, если
величина угла СЕА равна 370.
Биссектриса CK
угла АСЕ перпендикулярна отрезку АЕ. Найдите градусную меру угла САЕ, если
величина угла СЕА равна 370.
Ответ:______________________
5. Используя транспортир и угольник, постройте высоту DН и биссектрису BМ треугольника ABD, изображенного на рисунке.
II часть
Для записи решений и ответов каждого задания второй части используйте тетрадные листы в клетку. Запишите номер выполняемого задания, затем полное обоснованное решение и ответ. Каждое задание второй части оценивается от нуля до двух баллов.
6. На сторонах угла D отмечены точки М и К так, что DМ = DК. Точка Р лежит внутри угла D и РК = РМ . Докажите, что луч DР – биссектриса угла МDК .
7.
В
окружности с центром О хорда АС пересекает диаметр МК в
точке В, причем АВ=ВС, ![]() .
Найдите
.
Найдите ![]() .
.
Вариант II
1 часть
В каждом задании первой части необходимо записать верный ответ, в отведенном для этого месте. Каждый верный ответ оценивается в один балл.
1. ![]() В треугольниках
АВС и МРК помечены равные элементы. Равенство каких элементов нужно добавить,
чтобы треугольники были равны по второму признаку равенства треугольников?
В треугольниках
АВС и МРК помечены равные элементы. Равенство каких элементов нужно добавить,
чтобы треугольники были равны по второму признаку равенства треугольников?
1) ВС=РМ
2) АС=МР
3) Угол А равен углу К
4) Угол А равен углу Р
Ответ:______________________
2. В равнобедренном треугольнике АВС АВ=ВС. Периметр треугольника равен 23 см. Найдите основание треугольника, если его боковая сторона равна 8,6 см.
Ответ:______________________
3. Найдите длины сторон треугольника АВС, если разность сторон АВ и АС равна 10 см, периметр треугольника – 38 см, углы А и С равны.
Ответ:______________________
4. Построили прямую КМ, на ней отметили точку В. Из этой точки провели к прямой перпендикуляр ВА так, что АК=АМ. Найдите длину отрезка ВК, если ВМ=10 см.
Ответ:______________________
5.
![]() Используя транспортир и угольник, постройте высоту ВН
и биссектрису АМ треугольника ABD,
изображенного на рисунке.
Используя транспортир и угольник, постройте высоту ВН
и биссектрису АМ треугольника ABD,
изображенного на рисунке.
II часть
Для записи решений и ответов каждого задания второй части используйте тетрадные листы в клетку. Запишите номер выполняемого задания, затем полное обоснованное решение и ответ. Каждое задание второй части оценивается от нуля до двух баллов.
6.
Луч
AD – биссектриса угла А. На сторонах угла А отмечены
точки В и С так, что ![]() .
Докажите, что АВ = АС .
.
Докажите, что АВ = АС .
7.
В
окружности с центром О проведены диаметры АВ и СК, причем ![]() Найдите
Найдите ![]() .
.
Инструкция по проверке и оценке работ
|
№ задания |
Планируемый результат |
Правильный ответ |
Критерии оценивания / Максимальный балл |
|
|
Вариант1 |
Вариант2 |
|||
|
1 |
Оперировать на базовом уровне понятиями: равенство фигур, равные фигуры, равенство треугольников |
1 |
3 |
1 балл |
|
2 |
Решение задач на свойства равнобедренного треугольника |
6,7см |
5,8 см |
1 балл |
|
3 |
Решение задач на применение признака равнобедренного треугольника |
11 см, 33 см, 33 см |
6 см, 16 см, 16 см |
1 балл |
|
4 |
Решение задач на применение признака равнобедренного треугольника |
370 |
10 см |
1 балл |
|
5 |
Построение биссектрисы, медианы, высоты треугольника |
|
|
1 балл |
|
6 |
Решение задачи на применение признаков равенства треугольников |
|
|
2 балла - доказательство верное, все шаги обоснованы, 1 балл - доказательство в целом верное, но содержит неточности |
|
7 |
Решение задач на применение признака равнобедренного треугольника, элементов и свойств окружности |
800 |
300 |
2 балла - ход решения верный, все его шаги выполнены правильно, получен верный ответ 1 балл - ход решения верный, все его шаги выполнены правильно, но даны неполные объяснения или допущена одна вычислительная ошибка |
Контрольная работа № 3 «Параллельные прямые»
План контрольной работы
|
№ задания |
КЭС (код) |
Раздел программы (содержательная линия) |
Проверяемый планируемый результат |
Уровень сложности |
Тип задания |
Время выполнения (мин) |
Максимальный балл |
|
1 |
7.1.2 |
Геометрические фигуры
|
Оперировать на базовом уровне понятиями: углы при параллельных прямых |
Базовый |
Со свободным, кратким однозначным ответом |
5 |
1 балл |
|
2 |
7.1.3 |
Отношения. Признаки параллельности прямых
|
Свободно оперировать понятиями признаки параллельности прямых. |
Базовый |
С выбором ответа |
5 |
1 балл |
|
3 |
7.1.2 |
Геометрические фигуры. Свойства параллельных прямых |
Решать задачи на применение свойств параллельных прямых |
Базовый |
Со свободным, кратким однозначным ответом |
5 |
1 балл |
|
4 |
7.1.2 |
Измерения и вычисления. Признаки параллельности прямых. Свойства параллельных прямых |
Решать задачи на применение свойств параллельных прямых |
Базовый |
Со свободным, кратким однозначным ответом |
5 |
1 балл |
|
5 |
7.1.2 |
Измерения и вычисления. Признаки параллельности прямых. Свойства параллельных прямых |
Геометрические факты для решения задач |
Базовый |
Со свободным, кратким однозначным ответом |
5 |
1 балл |
|
6 |
7.1.3 |
Отношения. Признаки и свойства параллельных прямых |
Геометрические факты для решения задач, в том числе, предполагающих несколько шагов решения |
Повышенный |
С развернутым ответом |
7 |
2 балла |
|
7 |
7.1.3 |
Отношения. Признаки параллельности прямых
|
Геометрические факты для решения задач, в том числе, предполагающих несколько шагов решения |
Повышенный |
С развернутым ответом |
8 |
2 балла |
|
|
|
|
|
|
|
40 мин |
9 баллов |
Вариант I
1 часть
В каждом задании первой части необходимо записать верный ответ, в отведенном для этого месте. Каждый верный ответ оценивается в один балл.
1. ![]() На рисунке две
прямые пересечены секущей. Назовите угол, соответственный углу 6.
На рисунке две
прямые пересечены секущей. Назовите угол, соответственный углу 6.
Ответ:______________________
![]()
2.
На
рисунке прямые m,
n, l
пересечены прямой k,
![]() Какие из прямых параллельны?
Какие из прямых параллельны?
1)m и n
2)m и l
3)n и l
4)m и k
![]() Ответ:______________________
Ответ:______________________
3.
На
рисунке прямая DF параллельна
прямой АВ. Используя данные рисунка, найдите ![]() .
.
Ответ:______________________
![]()
4. По данным рисунка найдите х.
Ответ:______________________
5. При пересечении двух параллельных прямых секущей образовались односторонние углы, один из которых в 5 раз больше другого. Найдите больший из этих углов.
Ответ:______________________
II часть
Для записи решений и ответов каждого задания второй части используйте тетрадные листы в клетку. Запишите номер выполняемого задания, затем полное обоснованное решение и ответ. Каждое задание второй части оценивается от нуля до двух баллов.
6.
Боковые
стороны равнобедренного треугольника АВС пересекает прямая МК, параллельная
основанию АВ. Найдите углы ![]() и
и ![]() треугольника МСК, если
треугольника МСК, если ![]()
7. Точки Р и F лежат по разные стороны от прямой TL. Докажите, что если PT|| FL, и PT=FL, то ΔPTL=ΔFLT.
Вариант II
1 часть
В каждом задании первой части необходимо записать верный ответ, в отведенном для этого месте. Каждый верный ответ оценивается в один балл.
![]()
1. На рисунке две прямые пересечены секущей. Назовите угол, накрест лежащий углу 3.
Ответ:______________________
2.
![]() На рисунке прямые m,
n, l
пересечены прямой k,
На рисунке прямые m,
n, l
пересечены прямой k,
![]() Какие из прямых параллельны?
Какие из прямых параллельны?
1) m и n
2) m и l
3) n и l
4) m и k
![]()
Ответ:______________________
3.
На
рисунке прямая DF параллельна
прямой ВС. Используя данные рисунка, найдите ![]() .
.
Ответ:______________________
4.
![]() По данным рисунка найдите х.
По данным рисунка найдите х.
Ответ:______________________
5. При пересечении двух параллельных прямых секущей образовались односторонние углы, один из которых на 200 меньше другого. Найдите больший из этих углов.
Ответ:______________________
II часть
Для записи решений и ответов каждого задания второй части используйте тетрадные листы в клетку. Запишите номер выполняемого задания, затем полное обоснованное решение и ответ. Каждое задание второй части оценивается от нуля до двух баллов.
6.
Прямая
МК параллельна основанию ВС равнобедренного треугольника АВС. Найдите
углы ![]() и
и ![]() треугольника МАК, если
треугольника МАК, если ![]()
7. АВ
и МК – диаметры окружности. Докажите, что АМ || ВК и найдите ![]() , если
, если ![]() .
.
Инструкция по проверке и оценке работ
|
№ задания |
Планируемый результат |
Правильный ответ |
Критерии оценивания / Максимальный балл |
|
|
Вариант1 |
Вариант2 |
|||
|
1 |
Оперировать на базовом уровне понятиями: углы при пересечении прямых |
2 |
2 |
1 балл |
|
2 |
Решение задач на признаки параллельности прямых |
3 |
2 |
1 балл |
|
3 |
Решение задач на применение признаков и свойств параллельных прямых |
410 |
410 |
1 балл |
|
4 |
Решение задач на применение признаков и свойств параллельных прямых |
72 |
56 |
1 балл |
|
5 |
Решение задач на применение признаков и свойств параллельных прямых |
1500 |
1000 |
1 балл |
|
6 |
Решение задач на применение признаков и свойств параллельных прямых |
460, 730 |
650, 780 |
2 балла - ход решения верный, все его шаги выполнены правильно, получен верный ответ 1 балл - ход решения верный, все его шаги выполнены правильно, но даны неполные объяснения или допущена одна вычислительная ошибка
|
|
7 |
Решение задач на применение признаков и свойств параллельных прямых |
|
|
2 балла - доказательство верное, все шаги обоснованы, 1 балл - доказательство в целом верное, но содержит неточности |
Контрольная работа № 4 «Прямоугольные треугольники»
План контрольной работы
|
№ задания |
КЭС (код) |
Раздел программы (содержательная линия) |
Проверяемый планируемый результат |
Уровень сложности |
Тип задания |
Время выполнения (мин) |
Максимальный балл |
|
1 |
7.5.1 |
Измерения и вычисления
|
оперировать на базовом уровне понятиями: расстояние от точки до прямой |
Базовый |
Со свободным, кратким однозначным ответом |
5 |
1 балл |
|
2 |
7.2.3 |
Измерения и вычисления. Свойства прямоугольного треугольника
|
Оперировать на базовом уровне свойствами прямоугольного треугольника |
Базовый |
Со свободным, кратким однозначным ответом |
5 |
1 балл |
|
3 |
7.2.3 |
Геометрические фигуры. Перпендикуляр |
Решать задачи на применение свойств прямоугольных треугольников |
Базовый |
Со свободным, кратким однозначным ответом |
5 |
1 балл |
|
4 |
7.2.3 |
Измерения и вычисления. Свойства прямоугольного треугольника
|
Задачи на применение свойств прямоугольных треугольников |
Базовый |
Со свободным, кратким однозначным ответом |
5 |
1 балл |
|
5 |
7.2.3 |
Измерения и вычисления. Признаки равенства прямоугольных треугольников
|
Задачи на применение свойств прямоугольных треугольников |
Базовый |
Со свободным, кратким однозначным ответом |
5 |
1 балл |
|
6 |
7.2.3 |
Измерения и вычисления. Свойства прямоугольного треугольника
|
Геометрические факты для решения задач, в том числе, предполагающих несколько шагов решения |
Повышенный |
С развернутым ответом |
7 |
2 балла |
|
7 |
7.2.3 |
Измерения и вычисления. Свойства прямоугольного треугольника
|
Геометрические факты для решения задач, в том числе, предполагающих несколько шагов решения |
Повышенный |
С развернутым ответом |
8 |
2 балла |
|
|
|
|
|
|
|
40 мин |
9 баллов |
Вариант I
1 часть
В каждом задании первой части необходимо записать верный ответ, в отведенном для этого месте. Каждый верный ответ оценивается в один балл.
1. В треугольнике АВС высоты равны: АН=12, ВМ=10, СР=9. Найдите расстояние от точки А до прямой ВС.
Ответ:______________________
2.
Катет
ВС прямоугольного треугольника АВС равен 18, ![]() . Найдите гипотенузу.
. Найдите гипотенузу.
Ответ:______________________
![]()
3. По данным рисунка найдите расстояние между прямыми МК и РТ.
Ответ:_____________________
4. Один из острых углов прямоугольного треугольника на 150 больше другого острого угла. Найдите величину меньшего острого угла.
Ответ:______________________
5.
В
прямоугольном треугольнике АВС с прямым углом С проведена высота СН. АС=8.
Найдите длину отрезка АН, если ![]() .
.
Ответ:______________________
II часть
Для записи решений и ответов каждого задания второй части используйте тетрадные листы в клетку. Запишите номер выполняемого задания, затем полное обоснованное решение и ответ. Каждое задание второй части оценивается от нуля до двух баллов.
6. В прямоугольном треугольнике один из углов равен 600, сумма гипотенузы и меньшего из катетов равна 36,6 см. Найдите гипотенузу прямоугольного треугольника.
7. В прямоугольном треугольнике угол равен 500. Найдите угол между высотой и медианой, проведенными к гипотенузе.
Вариант II
1 часть
В каждом задании первой части необходимо записать верный ответ, в отведенном для этого месте. Каждый верный ответ оценивается в один балл.
1. В треугольнике МРК высоты равны: МС=7, ВР=9, КЕ=10. Найдите расстояние от точки Р до прямой МК.
Ответ:______________________
2.
Гипотенуза
прямоугольного треугольника МОР равна 18, ![]() .
Найдите катет МР.
.
Найдите катет МР.
Ответ:______________________
3.
![]() По данным рисунка найдите расстояние между прямыми АВ
и CD.
По данным рисунка найдите расстояние между прямыми АВ
и CD.
Ответ:______________________
4. Один из острых углов прямоугольного треугольника на 440 меньше другого острого угла. Найдите величину большего острого угла.
Ответ:______________________
5.
В
прямоугольном треугольнике КМР с прямым углом М проведена высота МН. КН=13.
Найдите длину отрезка МК, если ![]() .
.
Ответ:______________________
II часть
Для записи решений и ответов каждого задания второй части используйте тетрадные листы в клетку. Запишите номер выполняемого задания, затем полное обоснованное решение и ответ. Каждое задание второй части оценивается от нуля до двух баллов.
6. В прямоугольном треугольнике один из углов равен 300, разность гипотенузы и меньшего из катетов равна 18,3 см. Найдите гипотенузу прямоугольного треугольника.
7. В прямоугольном треугольнике угол равен 400. Найдите угол между высотой и медианой, проведенными к гипотенузе.
Инструкция по проверке и оценке работ
|
№ задания |
Планируемый результат |
Правильный ответ |
Критерии оценивания / Максимальный балл |
|
|
Вариант1 |
Вариант2 |
|||
|
1 |
Оперировать на базовом уровне понятиями: свойства прямоугольного треугольника |
12 |
9 |
1 балл |
|
2 |
Решение задач на применение свойств прямоугольного треугольника |
36 |
9 |
1 балл |
|
3 |
Решение задач на применение свойств прямоугольного треугольника |
17 |
11 |
1 балл |
|
4 |
Решение задач на применение свойств прямоугольного треугольника |
37,5 |
670 |
1 балл |
|
5 |
Решение задач на применение признаков прямоугольного треугольника |
4 |
26 |
1 балл |
|
6 |
Решение задач на применение свойств прямоугольного треугольника |
24,4 |
36,6 |
2 балла - ход решения верный, все его шаги выполнены правильно, получен верный ответ 1 балл - ход решения верный, все его шаги выполнены правильно, но даны неполные объяснения или допущена одна вычислительная ошибка
|
|
7 |
Решение задач на применение свойств прямоугольного треугольника |
100 |
100 |
2 балла - ход решения верный, все его шаги выполнены правильно, получен верный ответ 1 балл - ход решения верный, все его шаги выполнены правильно, но даны неполные объяснения или допущена одна вычислительная ошибка |
Контрольная работа № 5 «Соотношения меду сторонами и углами треугольника»
План контрольной работы
|
№ задания |
КЭС (код) |
Раздел программы (содержательная линия) |
Проверяемый планируемый результат |
Уровень сложности |
Тип задания |
Время выполнения (мин) |
Максимальный балл |
|
1 |
7.2.2 |
Свойства и признаки равнобедренного треугольника |
Решать задачи на применение свойств равнобедренного треугольника |
Базовый |
Со свободным, кратким однозначным ответом |
5 |
1 балл |
|
2 |
7.2.6 |
Зависимость между величинами сторон и углов треугольника |
Решать задачи на зависимость между величинами сторон и углов треугольника |
Базовый |
Со свободным, кратким однозначным ответом |
5 |
1 балл |
|
3 |
7.2.6 |
Сумма углов треугольника |
Решать задачи используя сумму углов треугольника |
Базовый |
Со свободным, кратким однозначным ответом |
5 |
1 балл |
|
4 |
7.2.5 |
Неравенство треугольников |
Использовать неравенство треугольников |
Базовый |
Со свободным, кратким однозначным ответом |
5 |
1 балл |
|
5 |
7.2.2 |
Свойства и признаки равнобедренного треугольника |
Решать задачи на применение свойств равнобедренного треугольника |
Базовый |
Со свободным, кратким однозначным ответом |
5 |
1 балл |
|
6 |
7.2.1 |
Высота, медиана, биссектриса, средняя линия треугольника; точки пересечения |
Решать задачи на применение свойств треугольника |
Повышенный |
С развернутым ответом |
7 |
2 балла |
|
7 |
7.2.6 |
Сумма углов треугольника |
Решать задачи используя сумму углов треугольника |
Повышенный |
С развернутым ответом |
7 |
2 балла |
Вариант I
1 часть
В каждом задании первой части необходимо записать верный ответ, в отведенном для этого месте. Каждый верный ответ оценивается в один балл.
1. В равнобедренном треугольнике угол при основании равен 500. Найдите угол при вершине.
Ответ:______________________
2. Найдите углы треугольника, если их градусные меры относятся как 7 : 5 : 3.
Ответ:______________________
3. Один из внешних углов треугольника равен 1340. Найдите углы треугольника, не смежные с ним, если один из них на 200 больше другого. В ответ запишите больший угол.
Ответ:______________________
4. Какие из треугольников с заданными сторонами существуют?
1) 3; 4; 7
2) 6; 10; 3
3) 3; 4; 5
4) 8; 12; 18
Ответ:______________________
5. В треугольнике АВС проведена биссектриса CМ, причем СМ=МВ. Найдите градусную меру угла АВС, если величина угла АСВ равна 540.
![]()
Ответ:______________________
II часть
Для записи решений и ответов каждого задания второй части используйте тетрадные листы в клетку. Запишите номер выполняемого задания, затем полное обоснованное решение и ответ. Каждое задание второй части оценивается от нуля до двух баллов.
6. Один из углов треугольника равен 680. Найдите меньший угол между биссектрисами двух других углов треугольника.
7. Внешний угол равнобедренного треугольника в три раза больше внутреннего угла, смежного с ним. Найдите углы треугольника.
Вариант II
1 часть
В каждом задании первой части необходимо записать верный ответ, в отведенном для этого месте. Каждый верный ответ оценивается в один балл.
1. В равнобедренном треугольнике угол при вершине равен 800. Найдите угол при основании.
Ответ:______________________
2. Найдите углы треугольника, если их градусные меры относятся как 4 : 6 : 2.
Ответ:______________________
3. Один из внешних углов треугольника равен 1420. Найдите углы треугольника, не смежные с ним, если один из них на 340 больше другого. В ответ запишите меньший угол.
Ответ:______________________
4. Какие из треугольников с заданными сторонами существуют?
1) 5; 6; 7
2) 1; 1; 3
3) 6; 8; 10
4) 3; 4; 7
Ответ:______________________
5.
![]() В треугольнике АВС проведена биссектриса CМ,
причем СМ=МВ. Найдите градусную меру угла АВС, если величина угла
АСВ равна 480.
В треугольнике АВС проведена биссектриса CМ,
причем СМ=МВ. Найдите градусную меру угла АВС, если величина угла
АСВ равна 480.
Ответ:______________________
II часть
Для записи решений и ответов каждого задания второй части используйте тетрадные листы в клетку. Запишите номер выполняемого задания, затем полное обоснованное решение и ответ. Каждое задание второй части оценивается от нуля до двух баллов.
6. В равнобедренном треугольнике проведена высота к боковой стороне. Угол между высотой и основанием равен 160. Найдите углы треугольника.
7. Внешний угол равнобедренного треугольника в пять раз больше внутреннего угла, смежного с ним. Найдите углы треугольника.
Инструкция по проверке и оценке работ
|
№ задания |
Планируемый результат |
|
Правильный ответ |
Критерии оценивания / Максимальный балл |
|
|
|
Вариант1 |
Вариант2 |
|||
|
1 |
Решение задач на применение свойств равнобедренного треугольника |
Решать задачи на применение свойств равнобедренного треугольника |
800 |
500 |
1 балл |
|
2 |
Решение задач на зависимость между величинами сторон и углов треугольника |
Решать задачи на зависимость между величинами сторон и углов треугольника |
|
|
1 балл |
|
3 |
Решение задач на сумму углов треугольника |
Решать задачи используя сумму углов треугольника |
770 |
540 |
1 балл |
|
4 |
Решение задач на неравенство треугольников |
Использовать неравенство треугольников |
3; 4 |
1; 3 |
1 балл |
|
5 |
Решение задач на применение свойств равнобедренного треугольника |
Решать задачи на применение свойств равнобедренного треугольника |
170 |
240 |
1 балл |
|
6 |
Решение задач на применение свойств треугольника |
Решать задачи на применение свойств треугольника |
|
|
2 балла - ход решения верный, все его шаги выполнены правильно, получен верный ответ 1 балл - ход решения верный, все его шаги выполнены правильно, но даны неполные объяснения или допущена одна вычислительная ошибка
|
|
7 |
Решение задач на сумму углов треугольника |
Решать задачи используя сумму углов треугольника |
|
|
2 балла - ход решения верный, все его шаги выполнены правильно, получен верный ответ 1 балл - ход решения верный, все его шаги выполнены правильно, но даны неполные объяснения или допущена одна вычислительная ошибка |
Алгебра 8 класс. Диагностическая работа (входная)
План диагностической работы
|
№ задания |
КЭС (код) |
Раздел программы (содержательная линия) |
Проверяемый планируемый результат |
Уровень сложности |
Тип задания |
Время выполнения (мин) |
Максимальный балл |
|
1 |
2.2.1 |
Тождественные преобразования |
Выполнять несложные преобразования для вычисления значений числовых выражений, содержащих степени с натуральным показателем |
Базовый |
Со свободным, кратким однозначным ответом |
1 |
1 балл |
|
2 |
2.2.1 |
Тождественные преобразования |
Выполнять несложные преобразования для вычисления значений числовых выражений, содержащих степени с натуральным показателем |
Базовый |
Со свободным, кратким однозначным ответом |
1 |
1 балл |
|
3 |
2.2.1 |
Числа и дроби |
Выполнять вычисления с рациональными числами, сочетая устные и письменные приёмы вычислений |
Базовый |
Со свободным, кратким однозначным ответом |
3 |
1 балл |
|
4 |
3.1.1 |
Уравнения и неравенства |
Решать линейные уравнения |
Базовый |
Со свободным, кратким однозначным ответом |
2 |
1 балл |
|
5 |
5.1.3 |
Функции |
По графику линейной функции определять знаки коэффициентов к и b |
Базовый |
С выбором верного ответа из нескольких вариантов |
1 |
1 балл |
|
6 |
3.1.1 |
Текстовые задачи |
Решать несложные сюжетные задачи разных типов на все арифметические действия |
Базовый |
Со свободным, кратким однозначным ответом |
3 |
1 балл |
|
7 |
2.3.2
|
Тождественные преобразования |
Выполнять несложные преобразования целых выражений: раскрывать скобки, приводить подобные слагаемые |
Базовый |
Со свободным, кратким однозначным ответом |
2 |
1 балл |
|
8 |
8.1.2 |
Статистика и теория вероятности |
Читать информацию, представленную в виде таблицы, определять основные статистические характеристики числовых наборов |
Базовый |
Со свободным, кратким однозначным ответом |
2 |
1 балл |
|
9 |
2.3.4 |
Тождественные преобразования |
Выполнять несложные преобразования целых выражений: раскладывать на множители способом группировки |
Базовый |
С выбором верного ответа из нескольких вариантов |
3 |
1 балл |
|
10 |
1.5.4 |
Статистика и теория вероятности |
Читать информацию, представленную в виде диаграммы |
Базовый |
Со свободным, кратким однозначным ответом |
3 |
1 балл |
|
11 |
5.1.1 |
Функции |
Находить значение аргумента по заданному значению функции в несложных ситуациях |
Базовый |
Со свободным, кратким однозначным ответом |
2 |
1 балл |
|
12 |
5.1.7 |
Уравнения и неравенства |
Решать системы несложных линейных уравнений алгебраически или графически |
Базовый |
Со свободным, кратким однозначным ответом |
2 |
1 балл |
|
13 |
2.3.3 |
Уравнения и неравенства |
Решать уравнения разложением на множители, используя вынесение общего множителя за скобку, формулы сокращенного умножения |
Повышенный |
С развернутым ответом |
4 |
2 балла 2 балла получен верный обоснованный ответ,. 1 балл при верных рассуждениях допущена вычислительная ошибка, возможно приведшая к неверному ответу. 0 баллов другие случаи, не соответствующие указанным критериям |
|
14 |
5.1.6 |
Функции |
Строить график линейной функции с модулем |
Повышенный |
С развернутым ответом |
6 |
2 балла 2 балла получен верный обоснованный ответ,. 1 балл при верных рассуждениях допущена вычислительная ошибка, возможно приведшая к неверному ответу. 0 баллов другие случаи, не соответствующие указанным критериям |
|
15 |
1.5.3 |
Текстовые задачи |
Решать задачи разных типов (на работу, на движение), связывающих три величины, выделять эти величины и отношения между ними |
Повышенный |
С развернутым ответом |
8 |
2 балла 2 балла получен верный обоснованный ответ,. 1 балл при верных рассуждениях допущена вычислительная ошибка, возможно приведшая к неверному ответу. 0 баллов другие случаи, не соответствующие указанным критериям |
|
|
|
|
|
|
|
45 мин |
18 баллов |
Вариант I
1 часть
В каждом задании первой части необходимо записать верный ответ, в отведенном для этого месте. Каждый верный ответ оценивается в один балл.
1. Вычислите: ![]() ;
;
Ответ:________________________
2. Приведите одночлен
![]() к стандартному виду. В ответе укажите
степень полученного
одночлена.
к стандартному виду. В ответе укажите
степень полученного
одночлена.
Ответ:________________________
3. Значение какого из данных выражений является наименьшим?
![]() ;
; ![]()
Ответ:________________________
4. Решите уравнение: ![]() ;
;
Ответ:________________________
5. На рисунке
изображен график линейной функции вида ![]() .
.

Определите знаки коэффициентов k и b.
1)![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
Ответ:________________________
6. Решите задачу.
От Челябинска до Чебаркуля электричка движется на 6 минут дольше, чем от Чебаркуля до Златоуста. За сколько минут электричка дойдет от Челябинска до Чебаркуля, если весь путь от Челябинска до Златоуста (через Чебаркуль) занимает 3 часа 26 минут?
Ответ:________________________
7.
Найдите
значение выражения ![]() , при
, при ![]() .
.
Ответ:________________________
8. Результаты контрольной работы по математике в 7-а представлены в таблице:
|
Оценка |
«5» |
«4» |
«3» |
«2» |
|
Количество уч-ся. |
7 |
12 |
9 |
2 |
Найдите средний балл 7-а класса за эту контрольную работу.
Ответ:________________________
9. Разложите
многочлен ![]() на множители.
на множители.
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
Ответ:________________________
10. На диаграмме представлено распределение по природным зонам земель Челябинской области, общая площадь которой равна 88,3 тыс. км2.
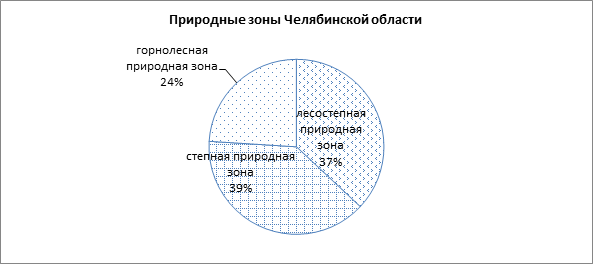
Площадь какой природной зоны примерно равна 33 тыс. км2?
1) Лесостепная природная зона.
2) Степная природная зона.
3) Горнолесная природная зона.
4) Лесостепная или степная природные зоны.
Ответ:________________________
11. Функция задана
формулой ![]() . При каком значении аргумента значение
функции равно 2?
. При каком значении аргумента значение
функции равно 2?
Ответ:________________________
12. Даны линейные функции ![]() и
и ![]() , которые
пересекаются в точке
, которые
пересекаются в точке ![]() . Найдите
. Найдите ![]() .
.
Ответ:________________________
II часть
Для записи решений и ответов каждого задания второй части используйте тетрадные листы в клетку. Запишите номер выполняемого задания, затем полное обоснованное решение и ответ. Каждое задание второй части оценивается от нуля до двух баллов.
13. Решите уравнение ![]() , разложив левую часть на множители.
, разложив левую часть на множители.
14. Постройте график функции ![]() .
.
15. Заказ по изготовлению деталей рабочий должен был выполнить за 20 дней. Но рабочий делал ежедневно по 2 детали сверх плана, а поэтому выполнил заказ за 18 дней. Сколько деталей сделал рабочий.
Вариант II
1 часть
В каждом задании первой части необходимо записать верный ответ, в отведенном для этого месте. Каждый верный ответ оценивается в один балл.
1. Вычислите: ![]()
Ответ:________________________
2. Приведите одночлен
![]() к стандартному виду. В ответе укажите
степень полученного одночлена.
к стандартному виду. В ответе укажите
степень полученного одночлена.
Ответ:________________________
3. Значение какого из данных выражений является наименьшим?
![]()
![]() ;
;
![]()
Ответ:________________________
4.
Решите
уравнение: ![]() ;
;
Ответ:________________________
5.
На
рисунке изображен график линейной функции вида ![]() .
.

Определите знаки коэффициентов k и b.
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
Ответ:________________________
6. Решите задачу.
От Челябинска до Миасса электричка движется на 46 минут дольше, чем от Миасса до Златоуста. За сколько минут электричка дойдет от Челябинска до Миасса, если весь путь от Челябинска до Златоуста (через Миасс) занимает 3 часа 26 минут?
Ответ:________________________
7. Найдите значение
выражения ![]() при
при ![]() .
.
Ответ:________________________
8. Результаты контрольной работы по математике в 7-в представлены в таблице:
|
Оценка |
«5» |
«4» |
«3» |
«2» |
|
Количество уч-ся. |
8 |
12 |
9 |
1 |
Найдите средний балл 7-в класса за эту контрольную работу.
Ответ:________________________
9. Разложите
многочлен ![]() на множители.
на множители.
5) ![]() ;
;
6) ![]() ;
;
7) ![]() ;
;
8) ![]() ;
;
Ответ:________________________
10. На диаграмме представлено распределение по природным зонам земель Челябинской области.

Площадь какой природной зоны составляет примерно равна 37% от общей площади земель Челябинской области?
5) Лесостепная природная зона.
6) Степная природная зона.
7) Горнолесная природная зона.
8) Лесостепная или степная природные зоны.
Ответ:________________________
11.
Функция
задана формулой ![]() . При каком значении аргумента значение
функции равно 2?
. При каком значении аргумента значение
функции равно 2?
Ответ:________________________
12.
Даны
линейные функции ![]() и
и ![]() , которые
пересекаются в точке
, которые
пересекаются в точке ![]() . Найдите
. Найдите ![]() .
.
Ответ:________________________
II часть
Для записи решений и ответов каждого задания второй части используйте тетрадные листы в клетку. Запишите номер выполняемого задания, затем полное обоснованное решение и ответ. Каждое задание второй части оценивается от нуля до двух баллов.
13.
Решите
уравнение ![]() , разложив левую часть на множители.
, разложив левую часть на множители.
14.
Постройте
график функции ![]() .
.
15.
Турист
рассчитал, что двигаясь с определенной скоростью, намеченный путь он пройдет за
2,5 часа. Но он увеличил скорость на ![]() , поэтому прошел путь за 2 часа. Найдите
длину пути.
, поэтому прошел путь за 2 часа. Найдите
длину пути.
Распределение заданий по разделам программ(ы)
|
№ п/п |
Раздел программы (содержательная линия) |
Количество заданий базового уровня сложности |
Количество заданий повышенного уровня сложности |
|
1. |
Числа и дроби |
1 |
|
|
2. |
Тождественные преобразования |
4 |
|
|
3. |
Уравнения и неравенства |
2 |
1 |
|
4. |
Статистика и теория вероятности |
2 |
|
|
5. |
Функции |
2 |
1 |
|
6. |
Текстовые задачи |
1 |
1 |
|
|
Всего |
12 |
3 |
Инструкция по проверке и оценке работ
|
№ задания |
Планируемый результат |
Правильный ответ |
Критерии оценивания / Максимальный балл |
||
|
Вариант1 |
Вариант2 |
||||
|
1 |
Рациональный счет, свойства степени |
|
|
1 балл |
|
|
2 |
Свойства степени, стандартный вид одночлена |
8 |
9 |
1 балл |
|
|
3 |
Рациональный счет, формулы сокращенного умножения |
2 |
3 |
1 балл |
|
|
4 |
Решение линейных уравнений |
0,5 |
2 |
1 балл |
|
|
5 |
График линейной функции, свойства линейной функции |
4 |
3 |
1 балл |
|
|
6 |
Решение текстовых задач с помощью уравнения или по действиям |
100 |
126 |
1 балл |
|
|
7 |
Преобразование буквенных выражений: раскрытие скобок, приведение подобных, вычисление значения выражения при заданном значении переменной |
2 |
12 |
1 балл |
|
|
8 |
Чтение информации, представленной в виде таблицы, определение основных статистических характеристик числовых наборов |
3,8 |
3,9 |
1 балл |
|
|
9 |
Разложение многочлена на множители |
4 |
2 |
1 балл |
|
|
10 |
установление отношений между множествами с помощью диаграмм |
1 |
1 |
1 балл |
|
|
11 |
Вычисление значения аргумента по заданному значению функции |
6 |
3 |
1 балл |
|
|
12 |
Определение координат точки пересечения прямых по построенному чертежу или решением системы уравнений |
6 |
5 |
1 балл |
|
|
13 |
Разложение многочлена на множители, решение уравнений старших степеней |
|
|
2 балла правильно выполнены преобразования, получен верный ответ. 1 балл решение доведено до конца, но допущена ошибка вычислительного характера или описка, с ее учетом дальнейшие шаги выполнены верно. 0 баллов другие случаи, не соответствующие указанным критериям |
|
|
14 |
Построение графика линейной функции с модулем |
См. рисунок |
См. рисунок |
2 балла верно и обоснованно построен график. 1 балл при верных рассуждениях допущена вычислительная ошибка, или описка, возможно приведшая к неверному ответу. 0 баллов другие случаи, не соответствующие указанным критериям |
|
|
15 |
Решение текстовых задач с помощью уравнения |
360 деталей |
10 км |
2 балла получен верный обоснованный ответ. 1 балл при верных рассуждениях допущена вычислительная ошибка, возможно приведшая к неверному ответу. 0 баллов другие случаи, не соответствующие указанным критериям |
|
Ответ к заданию 14 (построение графика)
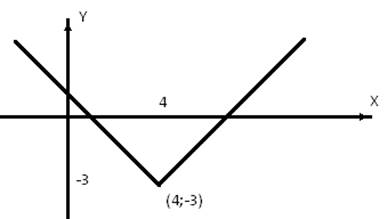

Контрольная работа № 1 «Рациональные дроби. Сумма и разность дробей»
План контрольной работы
|
№ задания |
КЭС (код) |
Раздел программы (содержательная линия) |
Проверяемый планируемый результат |
Уровень сложности |
Тип задания |
Время выполнения |
Максимальный балл |
|
1 |
2.4.1 |
Тождественные преобразования |
Выполнять несложные преобразования для сокращения дробей |
Базовый |
С кратким ответом |
3 мин |
1 балл |
|
2 |
2.4.2 |
Тождественные преобразования |
Выполнять различные действия с рациональными дробями |
Базовый |
С кратким ответом |
4 мин |
1 балл |
|
3 |
2.4.2 |
Тождественные преобразования |
Выполнять несложные преобразования для вычисления значений числовых выражений, содержащих степени с натуральным показателем |
Базовый |
С кратким ответом |
4 мин |
1 балл |
|
4 |
2.4.1 |
Тождественные преобразования |
выполнять несложные преобразования для сокращения дробей |
Базовый |
С выбором ответа |
5 мин |
1 балл |
|
5 |
2.4.1 |
Тождественные преобразования |
Находить область допустимых значений переменной |
Базовый |
С кратким ответом |
4 мин |
1 балл |
|
6 |
1.3.6 |
Числа |
Использовать свойства чисел и правила действий при выполнении вычислений; |
Повышенный |
С развернутым ответом |
10 мин |
2 балла |
|
7 |
2.4.1 |
Тождественные преобразования |
Выполнять преобразования для сокращения дробей, раскладывать выражения на множители |
Повышенный |
С развернутым ответом |
10 мин |
2 балла |
|
|
|
|
|
|
|
40 мин |
Общий балл |
Вариант I
1 часть
В каждом задании первой части необходимо записать верный ответ, в отведенном для этого месте. Каждый верный ответ оценивается в один балл.
1.
Сократите
дробь ![]() .
.
Ответ:_________
2.
Найдите
все значения переменной ![]() при которых НЕ
определено выражение
при которых НЕ
определено выражение ![]() .
.
Ответ:_________
3. Найдите
значение дроби ![]() .
.
Ответ:_________
4.
Запишите
частное в виде дроби и сократите полученную дробь: ![]()
1)
![]()
2)
![]()
3)
![]()
4)
![]()
Ответ:_________
5.
Найдите
все значения переменной, при которых значение дроби ![]() равно
нулю.
равно
нулю.
Ответ:__________
II часть
Для записи решений и ответов каждого задания второй части используйте тетрадные листы в клетку. Запишите номер выполняемого задания, затем полное обоснованное решение и ответ. Каждое задание второй части оценивается от нуля до двух баллов.
6.
Найдите
значение выражения: ![]() .
.
7.
Найдите
значение дроби ![]() при
при ![]() .
.
Вариант II
1 часть
В каждом задании первой части необходимо записать верный ответ, в отведенном для этого месте. Каждый верный ответ оценивается в один балл.
1.
Сократите дробь ![]() .
.
Ответ:_________
2.
Найдите все значения переменной ![]() при которых НЕ
определено выражение
при которых НЕ
определено выражение ![]() .
.
Ответ:_________
3.
Найдите значение дроби ![]() .
.
Ответ:_________
4.
Запишите частное в виде дроби и сократите полученную дробь: ![]()
1)
![]()
2)
![]()
3)
![]()
4)
![]()
Ответ:__________
5.
Найдите все значения переменной, при которых значение дроби ![]() равно нулю.
равно нулю.
Ответ:__________
II часть
Для записи решений и ответов каждого задания второй части используйте тетрадные листы в клетку. Запишите номер выполняемого задания, затем полное обоснованное решение и ответ. Каждое задание второй части оценивается от нуля до двух баллов.
6.
Найдите значение выражения: ![]() .
.
7.
Найдите значение дроби ![]() при
при ![]() .
.
Инструкция по проверке и оценке работ
|
№ задания |
Планируемый результат |
Правильный ответ |
Критерии оценивания / Максимальный балл |
|
|
1 вариант |
2 вариант |
|||
|
1 |
Сокращение дроби с использованием свойств степени |
|
|
За верный ответ 1 балл |
|
2 |
Выполнение действий с рациональными дробями |
2 |
3 |
За верный ответ 1 балл |
|
3 |
Сокращение дроби, вычисление значения выражения |
|
|
За верный ответ 1 балл |
|
4 |
Сокращение дроби с использованием свойств степени |
2 |
4 |
За верный ответ 1 балл |
|
5 |
Нахождение области допустимых значений переменной |
8 |
6 |
За верный ответ 1 балл |
|
6 |
Вычисление значения выражения, используя свойства степени и сокращая дроби |
|
|
2 балла получен верный обоснованный ответ. 1 балл при верных рассуждениях допущена вычислительная ошибка или описка, возможно приведшая к неверному ответу. 0 баллов другие случаи, не соответствующие указанным критериям |
|
7 |
Сокращение рациональной дроби, вычисление значения рациональной дроби |
2 |
2 |
2 балла получен верный обоснованный ответ. 1 балл при верных рассуждениях допущена вычислительная ошибка или описка, возможно приведшая к неверному ответу. 0 баллов другие случаи, не соответствующие указанным критериям |
|
|
|
|
Итого 9 |
|
Контрольная работа № 2 «Произведение и частное дробей»
План контрольной работы
|
№ задания |
КЭС (код) |
Раздел программы (содержательная линия) |
Проверяемый планируемый результат |
Уровень сложности |
Тип задания |
Время выполнения |
Максимальный балл |
|
1 а) |
2.4.2 |
Тождественные преобразования |
Выполнять произведение дробей, использовать сокращение |
Базовый |
С кратким ответом |
5 мин |
1 балл |
|
1 б) |
2.4.2 |
Тождественные преобразования |
Выполнять деление дробей, использовать формулы сокращенного умножения |
Базовый |
С кратким ответом |
5 мин |
1 балл |
|
1 в) |
2.4.2 |
Тождественные преобразования |
Выполнять произведение дробей, использовать сокращение |
Базовый |
С кратким ответом |
5 мин |
1 балл |
|
1 г) |
2.4.2 |
Тождественные преобразования |
Выполнять произведение дробей, нахождение общего знаменателя |
Базовый |
С кратким ответом |
5 мин |
1 балл |
|
2 |
5.1.1 |
Функция |
Находить промежутки знакопостоянства квадратичной функции |
Базовый |
С кратким ответом |
10 мин |
1 балл |
|
3 |
2.4.3 |
Тождественные преобразования |
Выполнять действия с дробями, нахождение общего знаменателя, использовать формулы сокращенного умножения |
Повышенный |
С развернутым ответом |
10 мин |
2 балла |
|
|
|
|
|
|
|
40 мин |
Общий балл |
Вариант I
1 часть
В каждом задании первой части необходимо записать верный ответ, в отведенном для этого месте.
1. Представьте в виде дроби:
а)
![]()
![]() ;
;
Ответ: _______
б)
![]() : ( 18a2
b ) ;
: ( 18a2
b ) ;
Ответ: _______
в)
![]() :
: ![]() ;
;
Ответ: _______
г)
![]()
![]() (
(
![]() +
+ ![]() )
)
Ответ: _______
2.
Постройте график функции y
= ![]() . Какова область
определения функции ? При каких значениях х функция принимает
отрицательные значения?
. Какова область
определения функции ? При каких значениях х функция принимает
отрицательные значения?
Ответ: _______
II часть
Для записи решений и ответов используйте тетрадные листы в клетку. Запишите номер выполняемого задания, затем полное обоснованное решение и ответ. Задание второй части оценивается от нуля до двух баллов.
3.
Докажите, что при всех значениях b ![]()
![]() 1
значение выражения (b
– 1)2 (
1
значение выражения (b
– 1)2 (![]() +
+ ![]() ) +
) + ![]()
не зависит от b
Вариант II
1 часть
В каждом задании первой части необходимо записать верный ответ, в отведенном для этого месте.
1. Представьте в виде дроби:
а)
![]() 17 x7y
;
17 x7y
;
Ответ: _______
б)
![]() :
: ![]() ;
;
Ответ: _______
в)
![]()
![]()
![]() ;
;
Ответ: _______
г)
![]()
![]() (
(
![]() -
- ![]() )
)
Ответ: _______
2.
Постройте график функции y
= - ![]() . Какова область
определения функции ? При каких значениях х функция принимает
положительные значения?
. Какова область
определения функции ? При каких значениях х функция принимает
положительные значения?
Ответ: _______
II часть
Для записи решений и ответов каждого задания второй части используйте тетрадные листы в клетку. Запишите номер выполняемого задания, затем полное обоснованное решение и ответ. Каждое задание второй части оценивается от нуля до двух баллов.
3.
Докажите, что при всех значениях х ![]()
![]() 2
значение выражения
2
значение выражения ![]() -
- ![]()
![]() (
(
![]() +
+ ![]() )
)
не зависит от х
Инструкция по проверке и оценке работ
|
№ задания |
Планируемый результат |
Правильный ответ |
Критерии оценивания / Максимальный балл |
|
|
1 вариант |
2 вариант |
|||
|
1 а) |
Выполнять произведение дробей, использовать сокращение |
|
|
За верный ответ 1 балл |
|
1 б) |
Выполнять деление дробей, использовать формулы сокращенного умножения |
|
|
За верный ответ 1 балл |
|
1 в) |
Выполнять произведение дробей, использовать сокращение |
|
|
За верный ответ 2 балла |
|
1 г) |
Выполнять произведение дробей, нахождение общего знаменателя |
|
|
За верный ответ 2 балла |
|
2 |
Находить промежутки знакопостоянства квадратичной функции |
|
|
За верный ответ 1 балл |
|
3 |
Доказательство тождества |
|
|
2 балла получен верный обоснованный ответ. 1 балл при верных рассуждениях допущена вычислительная ошибка или описка, возможно приведшая к неверному ответу. 0 баллов другие случаи, не соответствующие указанным критериям |
|
|
|
|
Итого 9 |
|
Контрольная работа № 3 «Арифметический квадратный корень и его свойства»
План контрольной работы
|
№ задания |
КЭС (код) |
Раздел программы (содержательная линия) |
Проверяемый планируемый результат |
Уровень сложности |
Тип задания |
Время выполнения |
Максимальный балл |
|
1 |
1.4.1 |
Числа |
Выполнять несложные арифметические действия с квадратными корнями |
Базовый |
С кратким ответом |
4 мин |
1 балл |
|
2 |
1.4.1 |
Числа |
Выполнять несложные арифметические действия с квадратными корнями |
Базовый |
С кратким ответом |
4 мин |
1 балл |
|
3 |
3.1.1 |
Уравнение и неравенства |
Решать уравнение по определению корня |
Базовый |
С кратким ответом |
4 мин |
1 балл |
|
4 |
1.4.1 |
Тождественные преобразования |
Выполнять простейшие преобразования с квадратным корнем |
Базовый |
С выбором ответа |
4 мин |
1 балл |
|
5 |
1.4.1 |
Числа |
Выполнять несложные арифметические действия с квадратными корнями |
Базовый |
С кратким ответом |
4 мин |
1 балл |
|
6 |
1.4.1 |
Числа |
Выполнять несложные арифметические действия с квадратными корнями, применяя свойства корня |
Повышенный |
С развернутым ответом |
10 мин |
2 балла |
|
7 |
1.4.1 |
Числа |
Выполнять несложные арифметические действия с квадратными корнями, применяя свойства корня |
Повышенный |
С развернутым ответом |
10 мин |
2 балла |
|
|
|
|
|
|
|
40 мин |
Общий балл |
Вариант I
1 часть
В каждом задании первой части необходимо записать верный ответ, в отведенном для этого месте. Каждый верный ответ оценивается в один балл.
1.
Вычислите
![]() .
.
Ответ:_________
2.
Упростите
![]() .
.
Ответ:_________
3.
Найдите
значение x, при котором верно
равенство ![]() .
.
Ответ:_________
4.
При
каких значениях ![]() имеет смысл выражение
имеет смысл выражение ![]() .
.
5) ни при каких
6) при любых
7) ![]()
8) ![]()
Ответ:_________
5.
Вычислите
![]() .
.
Ответ:__________
II часть
Для записи решений и ответов каждого задания второй части используйте тетрадные листы в клетку. Запишите номер выполняемого задания, затем полное обоснованное решение и ответ. Каждое задание второй части оценивается от нуля до двух баллов.
6. Выполните
действия: ![]() .
.
7.
Упростите выражение: ![]()
Вариант II
1 часть
В каждом задании первой части необходимо записать верный ответ, в отведенном для этого месте. Каждый верный ответ оценивается в один балл.
1.
Вычислите ![]() .
.
Ответ:_________
2.
Упростите ![]() .
.
Ответ:_________
3.
Найдите значение x, при котором верно
равенство ![]() .
.
Ответ:_________
4.
При каких значениях ![]() имеет смысл выражение
имеет смысл выражение ![]() .
.
5) ни при каких
6) при любых
7) ![]()
8) ![]()
Ответ:__________
5.
Вычислите ![]() .
.
Ответ:__________
II часть
Для записи решений и ответов каждого задания второй части используйте тетрадные листы в клетку. Запишите номер выполняемого задания, затем полное обоснованное решение и ответ. Каждое задание второй части оценивается от нуля до двух баллов.
6.
Выполните действия: ![]() .
.
7.
Упростите выражение: ![]()
Инструкция по проверке и оценке работ
|
№ задания |
Планируемый результат |
Правильный ответ |
Критерии оценивания / Максимальный балл |
|
|
1 вариант |
2 вариант |
|||
|
1 |
Вычисление арифметического квадратного корня |
|
|
За верный ответ 1 балл |
|
2 |
Выполнение действий с арифметическим квадратным корнем |
41 |
44 |
За верный ответ 1 балл |
|
3 |
Решение уравнение по определению квадратного корня |
|
|
За верный ответ 1 балл |
|
4 |
Выполнение преобразований квадратного корня |
3 |
3 |
За верный ответ 1 балл |
|
5 |
Выполнение действий с арифметическим квадратным корнем |
0 |
0 |
За верный ответ 1 балл |
|
6 |
Выполнение действий с арифметическим квадратным корнем |
6,5 |
6,5 |
2 балла получен верный обоснованный ответ. 1 балл при верных рассуждениях допущена вычислительная ошибка или описка, возможно приведшая к неверному ответу. 0 баллов другие случаи, не соответствующие указанным критериям |
|
7 |
Выполнение действий с арифметическим квадратным корнем с применением его свойств |
|
|
2 балла получен верный обоснованный ответ. 1 балл при верных рассуждениях допущена вычислительная ошибка или описка, возможно приведшая к неверному ответу. 0 баллов другие случаи, не соответствующие указанным критериям |
|
|
|
|
Итого 9 |
|
Контрольная работа № 4 «Преобразование выражений, содержащих квадратные корни»
План контрольной работы
|
№ задания |
КЭС (код) |
Раздел программы (содержательная линия) |
Проверяемый планируемый результат |
Уровень сложности |
Тип задания |
Время выполнения |
Максимальный балл |
|
1 |
1.3.4 |
Тождественные преобразования |
Выполнять сокращение рациональных дробей, содержащих квадратные корни |
Базовый |
С кратким ответом |
3 мин |
1 балл |
|
2 |
1.4.1 |
Тождественные преобразования |
Выполнять преобразования выражений с квадратными корнями, |
Базовый |
С кратким ответом |
4 мин |
1 балл |
|
3 |
1.3.4 |
Тождественные преобразования |
Выполнять преобразования выражений с квадратными корнями, |
Базовый |
С кратким ответом |
4 мин |
1 балл |
|
4 |
2.1.4 |
Тождественные преобразования |
Выполнять преобразования выражений с квадратными корнями, внесение множителя под знак корень |
Базовый |
С выбором ответа |
4 мин |
1 балл |
|
5 |
2.1.2 |
Тождественные преобразования |
Находить область допустимых значений |
Базовый |
С кратким ответом |
3 мин |
1 балл |
|
6 |
2.5.1 |
Тождественные преобразования |
Выполнять преобразования выражений с квадратными корнями. |
Повышенный |
С развернутым ответом |
12 мин |
2 балла |
|
7 |
1.4.5 |
Числа |
Выполнять преобразования выражений с квадратными корнями, сравнивать иррациональные числа |
Повышенный |
С развернутым ответом |
10 мин |
2 балла |
|
|
|
|
|
|
|
40 мин |
Общий балл |
Вариант I
1 часть
В каждом задании первой части необходимо записать верный ответ, в отведенном для этого месте. Каждый верный ответ оценивается в один балл.
1.
Сократите
дробь ![]() .
.
Ответ:_________
2.
Вынести
множитель за знак корня: ![]() .
.
Ответ:_________
3.
Упростите
выражение: ![]() .
.
Ответ:_________
4.
Внесите
множитель под знак корня: ![]() .
.
1) ![]()
2)
![]()
3)
![]()
4)
![]()
Ответ:_________
5.
При
каких ![]() имеет смысл выражение
имеет смысл выражение ![]() .
.
Ответ:__________
II часть
Для записи решений и ответов каждого задания второй части используйте тетрадные листы в клетку. Запишите номер выполняемого задания, затем полное обоснованное решение и ответ. Каждое задание второй части оценивается от нуля до двух баллов.
6. Упростите
выражение:  .
.
7.
Что меньше ![]() или
или ![]() ?
?
Вариант II
1 часть
В каждом задании первой части необходимо записать верный ответ, в отведенном для этого месте. Каждый верный ответ оценивается в один балл.
1.
Сократите дробь ![]() .
.
Ответ:_________
2.
Вынести множитель за знак корня: ![]() .
.
Ответ:_________
3.
Упростите выражение: ![]() .
.
Ответ:_________
4.
Внесите множитель под знак корня: ![]() .
.
9)
![]()
10) ![]()
11) ![]()
12) ![]()
Ответ:__________
1.
5.
При каких ![]() имеет смысл выражение
имеет смысл выражение ![]() .
.
Ответ:__________
II часть
Для записи решений и ответов каждого задания второй части используйте тетрадные листы в клетку. Запишите номер выполняемого задания, затем полное обоснованное решение и ответ. Каждое задание второй части оценивается от нуля до двух баллов.
6.
Упростите
выражение:  .
.
7.
Что меньше ![]() или
или ![]() ?
?
Инструкция по проверке и оценке работ
|
№ задания |
Планируемый результат |
Правильный ответ |
Критерии оценивания / Максимальный балл |
|
|
1 вариант |
2 вариант |
|||
|
1 |
Сокращение рациональной дроби |
|
|
За верный ответ 1 балл |
|
2 |
Вынесение множителя за знак корня |
|
|
За верный ответ 1 балл |
|
3 |
Преобразование рациональных выражений содержащих квадратные корни |
0 |
0 |
За верный ответ 1 балл |
|
4 |
Внесение множителя под знак корня |
3 |
3 |
За верный ответ 1 балл |
|
5 |
Определить область допустимых значений выражения |
0 |
0 |
За верный ответ 1 балл |
|
6 |
Преобразование рациональных выражений содержащих квадратные корни |
|
|
2 балла получен верный обоснованный ответ. 1 балл при верных рассуждениях допущена вычислительная ошибка или описка, возможно приведшая к неверному ответу. 0 баллов другие случаи, не соответствующие указанным критериям |
|
7 |
Преобразование рациональных выражений содержащих квадратные корни, выполнение сравнения иррациональных чисел |
|
|
2 балла получен верный обоснованный ответ. 1 балл при верных рассуждениях допущена вычислительная ошибка или описка, возможно приведшая к неверному ответу. 0 баллов другие случаи, не соответствующие указанным критериям |
|
|
|
|
Итого 9 |
|
Контрольная работа № 5 «Решение квадратных уравнений»
План контрольной работы
|
№ задания |
КЭС (код) |
Раздел программы (содержательная линия) |
Проверяемый планируемый результат |
Уровень сложности |
Тип задания |
Время выполнения |
Максимальный балл |
|
1 |
3.1.3 |
Уравнения и неравенства |
Решать квадратные уравнения |
Базовый |
С кратким ответом |
3 мин |
1 балл |
|
2 |
2.3.4 |
Уравнения и неравенства |
Применение теоремы Виета для квадратного уравнения |
Базовый |
С кратким ответом |
2 мин |
1 балл |
|
3 |
3.3.2 |
Текстовые задачи |
Решать не сложные текстовые задачи с помощью уравнения |
Базовый |
С кратким ответом |
5 мин |
1 балл |
|
4 |
3.1.3 |
Уравнения и неравенства |
Составлять квадратное уравнение с заданными корнями |
Базовый |
с выбором ответа |
5 мин |
1 балл |
|
5 |
2.3.4 |
Уравнения и неравенства |
Выполнение преобразований дробно-рациональных выражений, с разложением квадратного трехчлена на множители. Отбор корней. |
Базовый |
С кратким ответом |
3 мин |
1 балл |
|
6 |
3.1.5 |
Уравнения и неравенства |
Умение решать уравнение методом замены переменной, отбор корней |
Повышенный |
С развернутым ответом |
10 мин |
2 балла |
|
7 |
5.1.7 |
Функции |
Умение находить точку пересечения графиков функций с помощью уравнения |
Повышенный |
С развернутым ответом |
12 мин |
2 балла |
|
|
|
|
|
|
|
40 мин |
Общий балл |
Вариант I
1 часть
В каждом задании первой части необходимо записать верный ответ, в отведенном для этого месте. Каждый верный ответ оценивается в один балл.
1.
Какое
из чисел ![]() является корнем
уравнения
является корнем
уравнения ![]() , в ответ запишите это
число
, в ответ запишите это
число
Ответ:_________
2. Найдите
сумму корней уравнения ![]()
Ответ: _________
3. Решите задачу: Первое число на 4 больше второго, их произведение равно 96. В ответ запишите меньшее число.
Ответ: __________
4.
Среди
предложенных уравнений, выберите то, корнями которого являются числа ![]() .
.
1) ![]() ;
;
2) ![]() ;
;
3) ![]() ;
;
4) ![]() ;
;
Ответ:__________
5. Решите
уравнение ![]() , в ответ запишите корень
уравнения, если корней несколько, в ответ запишите их сумму.
, в ответ запишите корень
уравнения, если корней несколько, в ответ запишите их сумму.
Ответ:__________
II часть
Для записи решений и ответов каждого задания второй части используйте тетрадные листы в клетку. Запишите номер выполняемого задания, затем полное обоснованное решение и ответ. Каждое задание второй части оценивается от нуля до двух баллов.
6. Решите
уравнение: ![]()
7. При
каком значении параметра b
графики функций ![]() имеют только одну общую
точку.
имеют только одну общую
точку.
Вариант II
1 часть
В каждом задании первой части необходимо записать верный ответ, в отведенном для этого месте. Каждый верный ответ оценивается в один балл.
1.
Какое
из чисел ![]() является корнем
уравнения
является корнем
уравнения ![]() , в ответ запишите это
число
, в ответ запишите это
число
Ответ:__________
2. Найдите
произведение корней уравнения ![]()
Ответ: __________
3. Решите задачу: Сумма двух чисел равна 19, а их произведение равно 84. Найдите эти числа. В ответ запишите большее число.
Ответ: __________
4.
Среди
предложенных уравнений, выберите то, корнями которого являются числа ![]() .
.
1) ![]() ;
;
2) ![]() ;
;
3) ![]() ;
;
4) ![]() ;
;
Ответ:__________
5. Решите
уравнение ![]() , в ответ запишите корень
уравнения, если корней несколько, в ответ запишите их сумму.
, в ответ запишите корень
уравнения, если корней несколько, в ответ запишите их сумму.
Ответ:__________
II часть
Для записи решений и ответов каждого задания второй части используйте тетрадные листы в клетку. Запишите номер выполняемого задания, затем полное обоснованное решение и ответ. Каждое задание второй части оценивается от нуля до двух баллов.
6. Решите
уравнение: ![]()
7. При
каком значении параметра b
графики функций ![]() имеют только одну общую
точку.
имеют только одну общую
точку.
Инструкция по проверке и оценке работ
|
№ задания |
Планируемый результат |
Правильный ответ |
Критерии оценивания / Максимальный балл |
|
|
1 вариант |
2 вариант |
|||
|
1 |
Навыки решения квадратного уравнения |
|
|
За верный ответ 1 балл |
|
2 |
Применение теоремы Виета |
2 |
|
За верный ответ 1 балл |
|
3 |
Составление и решение квадратного уравнения по заданным условиям |
|
12 |
За верный ответ 1 балл |
|
4 |
Составление квадратного уравнения с заданными корнями |
3 |
3 |
За верный ответ 1 балл |
|
5 |
Разложение квадратного трехчлена на множители, отбор корней |
|
|
За верный ответ 1 балл |
|
6 |
Решение уравнений высших степеней с помощью замены переменной, отбор корней |
3; 7 |
3; 7 |
2 балла получен верный обоснованный ответ. 1 балл при верных рассуждениях допущена вычислительная ошибка или описка, возможно приведшая к неверному ответу. 0 баллов другие случаи, не соответствующие указанным критериям |
|
7 |
Нахождение точки пересечения графиков функций с помощью уравнения, анализ квадратного уравнения |
|
-1 |
2 балла получен верный обоснованный ответ. 1 балл при верных рассуждениях допущена вычислительная ошибка или описка, возможно приведшая к неверному ответу. 0 баллов другие случаи, не соответствующие указанным критериям |
|
|
|
|
Итого 9 |
|
Контрольная работа № 6 «Решение дробных рациональных уравнений»
План контрольной работы
|
№ задания |
КЭС (код) |
Раздел программы (содержательная линия) |
Проверяемый планируемый результат |
Уровень сложности |
Тип задания |
Время выполнения |
Максимальный балл |
|
1 |
2.3.4 |
Уравнения и неравенства |
Выполнение преобразований дробно-рациональных выражений. Отбор корней. |
Базовый |
С кратким ответом |
12 мин |
3 балла
|
|
2 |
2.3.4 |
Уравнения и неравенства |
Выполнение преобразований дробно-рациональных выражений. Отбор корней. |
Базовый |
С кратким ответом |
12 мин |
3 балла |
|
3 |
3.3.2 |
Текстовые задачи |
Решать задачи разных типов (на движение), связывающих три величины, выделять эти величины и отношения между ними |
Повышенный |
С развернутым ответом |
16 мин |
3 балла |
|
|
|
|
|
|
|
40 мин |
Общий балл |
Вариант I
1 часть
В каждом задании первой части необходимо записать верный ответ, в отведенном для этого месте.
1. Решите уравнение:
а)
![]()
![]() ;
;
Ответ: _______
б)
![]() +
+ ![]() = 3;
= 3;
Ответ: _______
II часть
Для записи решения и ответа второй части используйте тетрадные листы в клетку. Запишите номер выполняемого задания, затем полное обоснованное решение и ответ.
2. Из пункта А в пункт В велосипедист проехал по одной дороге длиной 27 км, а обратно возвращался по другой дороге, которая была короче первой на 7 км. Хотя на обратном пути велосипедист уменьшил скорость на 3 км/ч, он всё же на обратный путь затратил времени на 10 мин меньше, чем на путь из А в В. С какой скоростью ехал велосипедист из А в В?
Вариант II
1 часть
В каждом задании первой части необходимо записать верный ответ, в отведенном для этого месте.
1. Решите уравнение:
а)
![]()
![]() ;
;
Ответ: _______
б)
![]() +
+ ![]() = 2;
= 2;
Ответ: _______
II часть
Для записи решения и ответа второй части используйте тетрадные листы в клетку. Запишите номер выполняемого задания, затем полное обоснованное решение и ответ.
3. Катер прошел 12 км против течения реки и 5 км по течению. При этом он затратил столько времени, сколько ему потребовалось бы, если бы он шел 18 км по озеру. Какова собственная скорость катера, если известно, что скорость течения реки равна 3 км/ч?
Инструкция по проверке и оценке работ
|
№ задания |
Планируемый результат |
Правильный ответ |
Критерии оценивания / Максимальный балл |
|
|
1 вариант |
2 вариант |
|||
|
1 а) |
Преобразование дробно-рациональных выражений. Отбор корней. |
-4 |
-1 |
3 балла получен верный обоснованный ответ. 2 балла при верных рассуждениях допущена вычислительная ошибка или описка, возможно приведшая к неверному ответу. 1 балл другие случаи, не соответствующие указанным критериям |
|
1 б) |
Преобразование дробно-рациональных выражений. Отбор корней. |
|
2,5;8 |
3 балла получен верный обоснованный ответ. 2 балла при верных рассуждениях допущена вычислительная ошибка или описка, возможно приведшая к неверному ответу. 1 балл другие случаи, не соответствующие указанным критериям |
|
2 |
Решение текстовых задач с помощью дробно рациональных уравнений |
18 км/ч |
27 км/ч |
3 балла получен верный обоснованный ответ. 2 балла при верных рассуждениях допущена вычислительная ошибка или описка, возможно приведшая к неверному ответу. 1 балл другие случаи, не соответствующие указанным критериям |
|
|
|
|
Итого 9 |
|
Контрольная работа № 7 «Числовые неравенства и их свойства»
План контрольной работы
|
№ задания |
КЭС (код) |
Раздел программы (содержательная линия) |
Проверяемый планируемый результат |
Уровень сложности |
Тип задания |
Время выполнения |
Максимальный балл |
|
1 |
3.2.1 |
Уравнения и неравенства |
Проверять справедливость числовых равенств и неравенств |
Базовый |
С кратким ответом |
3 мин |
1 балл |
|
2 |
3.2.2 |
Уравнения и неравенства |
Решать несложные числовые неравенства |
Базовый |
С кратким ответом |
3 мин |
1 балл |
|
3 |
3.2.2 |
Уравнения и неравенства |
Решать несложные числовые неравенства, анализировать полученные корни |
Базовый |
С кратким ответом |
5 мин |
1 балл |
|
4 |
3.2.2 |
Функции |
Нахождение области допустимых значений переменной |
Базовый |
С выбором ответа |
5 мин |
1 балл |
|
5 |
3.3.1 |
Текстовые задачи |
Решать несложные текстовые задачи на проценты, применять свойства числовых неравенств |
Базовый |
С кратким ответом |
4 мин |
1 балл |
|
6 |
3.2.3 |
Уравнения и неравенства |
Решать числовые неравенства с модулем |
Повышенный |
С развернутым ответом |
10 мин |
2 балла |
|
7 |
3.1.3 |
Уравнения и неравенства |
Исследовать квадратное уравнение на количество корней |
Повышенный |
С развернутым ответом |
10 мин |
2 балла |
|
|
|
|
|
|
|
40 мин |
Общий балл |
Вариант I
1 часть
В каждом задании первой части необходимо записать верный ответ, в отведенном для этого месте. Каждый верный ответ оценивается в один балл.
1.
Какое
из указанных чисел -3; 0; 1,1;1,9; 3,2 является решением неравенства: ![]()
Ответ:_________
2.
Укажите
наибольшее натуральное число, при котором выполняется неравенство ![]() .
.
Ответ:_________
3.
Найдите
наибольшее значение x, при котором значение
многочлена ![]() принадлежит промежутку
принадлежит промежутку ![]() .
.
Ответ:_________
4.
Среди
предложенных значений переменной x
выберите то, при котором определено выражение: ![]() .
.
![]()
2. ![]()
3. ![]()
4. ![]()
Ответ:_________
5.
На
коробке конфет «Вечерний Челябинск» указано, что масса конфет без коробки ![]() . Известно, что масса
пустой коробки
. Известно, что масса
пустой коробки ![]() . Какую наибольшую массу
может иметь коробка с конфетами.
. Какую наибольшую массу
может иметь коробка с конфетами.
Ответ:__________
II часть
Для записи решений и ответов каждого задания второй части используйте тетрадные листы в клетку. Запишите номер выполняемого задания, затем полное обоснованное решение и ответ. Каждое задание второй части оценивается от нуля до двух баллов.
6. Решите
неравенство: ![]() .
.
7.
При каких значениях параметра ![]() уравнение
уравнение ![]() имеет два различных
действительных корня?
имеет два различных
действительных корня?
Вариант II
1 часть
В каждом задании первой части необходимо записать верный ответ, в отведенном для этого месте. Каждый верный ответ оценивается в один балл.
1.
Какое из указанных чисел -3; 0; 1,1;1,9; 3,2 является решением неравенства: ![]() .
.
Ответ:_________
2.
Укажите наименьшее натуральное число, при котором выполняется неравенство ![]() .
.
Ответ:_________
3.
Найдите наибольшее значение x,
при котором значение многочлена ![]() принадлежит промежутку
принадлежит промежутку![]() .
.
Ответ:_________
4.
Среди
предложенных значений переменной x
выберите то, при котором определено выражение: ![]() .
.
1. ![]()
2. ![]()
3. ![]()
4. ![]()
Ответ:__________
5.
На коробке конфет «Хозяйка Медной горы» указано, что масса конфет без коробки ![]() . Известно, что масса
пустой коробки
. Известно, что масса
пустой коробки ![]() . Какую наименьшую массу
может иметь коробка с конфетами.
. Какую наименьшую массу
может иметь коробка с конфетами.
Ответ:__________
II часть
Для записи решений и ответов каждого задания второй части используйте тетрадные листы в клетку. Запишите номер выполняемого задания, затем полное обоснованное решение и ответ. Каждое задание второй части оценивается от нуля до двух баллов.
6.
Решите неравенство: ![]() .
.
7.
При каких значениях параметра ![]() уравнение 2
уравнение 2![]() имеет два различных
действительных корня?
имеет два различных
действительных корня?
Инструкция по проверке и оценке работ
|
№ задания |
Планируемый результат |
Правильный ответ |
Критерии оценивания / Максимальный балл |
|
|
1 вариант |
2 вариант |
|||
|
1 |
Владение понятием неравенство, числовое неравенство, решение неравенства; |
1,9 |
1,9 |
За верный ответ 1 балл |
|
2 |
Решение числового неравенства, анализ корней |
5 |
1 |
За верный ответ 1 балл |
|
3 |
Решение числового неравенства, анализ корней |
0 |
2 |
За верный ответ 1 балл |
|
4 |
Нахождение ОДЗ переменной выражения |
3 |
4 |
За верный ответ 1 балл |
|
5 |
Решение текстовой задачи, нахождение числа по проценту, свойства числовых неравенств |
367 |
441 |
За верный ответ 1 балл |
|
6 |
Решение линейного неравенства с модулем |
|
|
2 балла получен верный обоснованный ответ. 1 балл при верных рассуждениях допущена вычислительная ошибка или описка, возможно приведшая к неверному ответу. 0 баллов другие случаи, не соответствующие указанным критериям |
|
7 |
Анализ корней квадратного уравнения, зависимость от дискриминанта. |
|
|
2 балла получен верный обоснованный ответ. 1 балл при верных рассуждениях допущена вычислительная ошибка или описка, возможно приведшая к неверному ответу. 0 баллов другие случаи, не соответствующие указанным критериям |
|
|
|
|
Итого 9 |
|
Контрольная работа № 8 «Решения неравенства с одной переменной и их системы»
План контрольной работы
|
№ задания |
КЭС (код) |
Раздел программы (содержательная линия) |
Проверяемый планируемый результат |
Уровень сложности |
Тип задания |
Время выполнения |
Максимальный балл |
|
1 а) |
3.2.2 |
Уравнения и неравенства |
Решать несложные числовые неравенства, анализировать полученные корни |
Базовый |
С кратким ответом |
3 мин |
1 балл |
|
1 б) |
3.2.2 |
Уравнения и неравенства |
Решать несложные числовые неравенства, анализировать полученные корни |
Базовый |
С кратким ответом |
3 мин |
1 балл |
|
1 в) |
3.2.2 |
Уравнения и неравенства |
Решать несложные числовые неравенства, анализировать полученные корни |
Базовый |
С кратким ответом |
4 мин |
1 балл |
|
2 а) |
3.2.4 |
Уравнения и неравенства |
Решать несложные системы числовых неравенств, анализировать полученные корни |
Базовый |
С кратким ответом |
4 мин |
1 балл |
|
2 б) |
3.2.4 |
Уравнения и неравенства |
Решать несложные системы числовых неравенств, анализировать полученные корни |
Базовый |
С кратким ответом |
6 мин |
1 балл |
|
3 |
3.2.4 |
Уравнения и неравенства |
Решать системы числовых неравенств, анализировать полученные корни |
Повышенный |
С развернутым ответом |
10 мин |
2 балла |
|
4 |
|
Уравнения и неравенства |
Решать системы числовых неравенств, анализировать полученные корни |
Повышенный |
С развернутым ответом |
10 мин |
2 балла |
|
|
|
|
|
|
|
40 мин |
Общий балл |
Вариант I
1 часть
В каждом задании первой части необходимо записать верный ответ, в отведенном для этого месте. Каждый верный ответ оценивается в один балл.
1. Решите неравенство:
а) ![]() х < 5;
х < 5;
Ответ: _______
б)
1 - 3х ![]() 0;
0;
Ответ: _______
в) 5(у –
1,2) – 4,6 ![]() 3у + 1.
3у + 1.
Ответ: _______
2. Решите систему неравенств:
![]()
![]() а) 2 х – 3
а) 2 х – 3 ![]() 0,
б) 3 - 2х
0,
б) 3 - 2х ![]() 1,
1,
7 х + 4 ![]() 0; 1,6
+ х
0; 1,6
+ х ![]() 2,9.
2,9.
Ответ: _______
II часть
Для записи решений и ответов каждого задания второй части используйте тетрадные листы в клетку. Запишите номер выполняемого задания, затем полное обоснованное решение и ответ. Каждое задание второй части оценивается от нуля до двух баллов.
3. При каких а значение дроби ![]() меньше соответствующего значения дроби
меньше соответствующего значения дроби ![]() ?
?
4. Найдите целые решения системы неравенств
![]() 6
– 2х
6
– 2х ![]() 3 (
х - 1),
3 (
х - 1),
6
- ![]()
![]() х.
х.
Вариант II
1 часть
В каждом задании первой части необходимо записать верный ответ, в отведенном для этого месте. Каждый верный ответ оценивается в один балл.
1. Решите неравенство:
а) ![]() х
х ![]() 2;
2;
Ответ: _______
б)
2 - 7х ![]() 0;
0;
Ответ: _______
в)
6(у – 1,5) – 3,4 ![]() 4у – 2,4
4у – 2,4
Ответ: _______
2. Решите систему неравенств:
![]()
![]() а) 4 х – 10
а) 4 х – 10 ![]() 10,
б) 1,4 + х
10,
б) 1,4 + х ![]() 1,5,
1,5,
3
х - 5 ![]() 1; 5
- 2х
1; 5
- 2х ![]() 2.
2.
Ответ: _______
II часть
Для записи решений и ответов каждого задания второй части используйте тетрадные листы в клетку. Запишите номер выполняемого задания, затем полное обоснованное решение и ответ. Каждое задание второй части оценивается от нуля до двух баллов.
3. При каких b значение дроби ![]() больше соответствующего значения дроби
больше соответствующего значения дроби ![]() ?
?
4. Найдите целые решения системы неравенств
![]() 10
– 4х
10
– 4х ![]() 3 (
1 - х ),
3 (
1 - х ),
3,5
+ ![]()
![]() 2х.
2х.
Инструкция по проверке и оценке работ
|
№ задания |
Планируемый результат |
Правильный ответ |
Критерии оценивания / Максимальный балл |
|
|
1 вариант |
2 вариант |
|||
|
1 а) |
Решение числового неравенства, анализ корней |
|
|
За верный ответ 1 балл |
|
1 б) |
Решение числового неравенства, анализ корней |
|
|
За верный ответ 1 балл |
|
1 в) |
Решение числового неравенства, анализ корней |
|
|
За верный ответ 1 балл |
|
2 а) |
Решение системы числовых неравенств, анализ корней |
|
|
За верный ответ 1 балл |
|
2 б) |
Решение системы числовых неравенств, анализ корней |
|
|
За верный ответ 1 балл |
|
3 |
Решение системы числовых неравенств, анализ корней |
При |
При |
2 балла получен верный обоснованный ответ. 1 балл при верных рассуждениях допущена вычислительная ошибка или описка, возможно приведшая к неверному ответу. 0 баллов другие случаи, не соответствующие указанным критериям |
|
4 |
Решение системы числовых неравенств, анализ корней |
2; 3; 4 |
3; 4; 5; 6; 7 |
2 балла получен верный обоснованный ответ. 1 балл при верных рассуждениях допущена вычислительная ошибка или описка, возможно приведшая к неверному ответу. 0 баллов другие случаи, не соответствующие указанным критериям |
|
|
|
|
Итого 9 |
|
Контрольная работа № 9 «Степень с целым показателем и её свойства»
План контрольной работы
|
№ задания |
КЭС (код) |
Раздел программы (содержательная линия) |
Проверяемый планируемый результат |
Уровень сложности |
Тип задания |
Время выполнения |
Максимальный балл |
|
1 |
2.2.1 |
Числа |
Выполнять несложные преобразования для вычисления значений числовых выражений, содержащих степени с целым отрицательным показателем; |
Базовый |
С кратким ответом |
3 мин |
1 балл |
|
2 |
2.2.1 |
Числа |
Выполнять несложные преобразования для вычисления значений числовых выражений, содержащих степени с целым отрицательным показателем; |
Базовый |
С кратким ответом |
3 мин |
1 балл |
|
3 |
2.3.3 |
Тождественные преобразования |
Выполнять преобразования выражений, раскладывать выражения на множители, сокращать дроби |
Базовый |
С кратким ответом |
5 мин |
1 балл |
|
4 |
2.2.1 |
Тождественные преобразования |
Выполнять несложные преобразования, используя свойства степени |
Базовый |
С выбором ответа |
5 мин |
1 балл |
|
5 |
2.2.1 |
Числа |
Сравнивать рациональные числа, используя свойства степени |
Базовый |
С кратким ответом |
4 мин |
1 балл |
|
6 |
2.2.1 |
Числа |
Выполнять преобразования для вычисления значений числовых выражений, содержащих степени с целым отрицательным показателем; |
Повышенный |
С развернутым ответом |
10 мин |
2 балла |
|
7 |
2.1.4 |
Тождественные преобразования |
Выполнять преобразования выражений, раскладывать выражения на множители, сокращать дроби |
повышенный |
С развернутым ответом |
10 мин |
2 балла |
|
|
|
|
|
|
|
40 мин |
Общий балл |
Вариант I
1 часть
В каждом задании первой части необходимо записать верный ответ, в отведенном для этого месте. Каждый верный ответ оценивается в один балл.
1. Вычислите
![]() .
.
Ответ:_________
2.
Найдите значение выражения ![]()
Ответ:_________
3.
Преобразуйте в дробь выражение ![]() .
.
Ответ:_________
4. Запишите
выражение в виде степени или произведения степеней ![]() .
.
1) ![]()
2) ![]()
3) ![]()
4) ![]()
Ответ:_________
5. Выберите
наименьшее из чисел, являющихся значениями выражений: ![]() или
или ![]()
Ответ:__________
II часть
Для записи решений и ответов каждого задания второй части используйте тетрадные листы в клетку. Запишите номер выполняемого задания, затем полное обоснованное решение и ответ. Каждое задание второй части оценивается от нуля до двух баллов.
6.
Вычислите:
![]() .
.
7.
Найдите значение выражения: ![]() при
при ![]()
Вариант II
1 часть
В каждом задании первой части необходимо записать верный ответ, в отведенном для этого месте. Каждый верный ответ оценивается в один балл.
1.
Вычислите ![]() ..
..
Ответ:_________
2.
Найдите значение выражения ![]()
Ответ:_________
3.
Преобразуйте в дробь выражение ![]() .
.
Ответ:_________
4.
Запишите выражение в виде степени или произведения степеней ![]() .
.
13)
![]()
14)
![]()
15)
![]()
16)
![]()
Ответ:__________
5.
Выберите наименьшее из чисел, являющихся значениями выражений: ![]() или
или ![]()
Ответ:__________
II часть
Для записи решений и ответов каждого задания второй части используйте тетрадные листы в клетку. Запишите номер выполняемого задания, затем полное обоснованное решение и ответ. Каждое задание второй части оценивается от нуля до двух баллов.
6.
Вычислите: ![]() .
.
7.
Найдите значение выражения: ![]() при
при ![]()
Инструкция по проверке и оценке работ
|
№ задания |
Планируемый результат |
Правильный ответ |
Критерии оценивания / Максимальный балл |
|
|
1 вариант |
2 вариант |
|||
|
1 |
Использование свойств степени, вычисление значения |
|
|
За верный ответ 1 балл |
|
2 |
Использование свойств степени, вычисление значения |
169 |
121 |
За верный ответ 1 балл |
|
3 |
Разложение многочлена на множители, сокращение дробей |
|
|
За верный ответ 1 балл |
|
4 |
Применение свойств степени для преобразования выражения |
4 |
4 |
За верный ответ 1 балл |
|
5 |
Сравнение чисел, используя свойства степени и свойства дроби |
B |
A |
За верный ответ 1 балл |
|
6 |
Вычисление значения выражения, используя свойства степени |
|
|
2 балла получен верный обоснованный ответ. 1 балл при верных рассуждениях допущена вычислительная ошибка или описка, возможно приведшая к неверному ответу. 0 баллов другие случаи, не соответствующие указанным критериям |
|
7 |
Преобразование выражения, вычисление значения выражения |
|
|
2 балла получен верный обоснованный ответ. 1 балл при верных рассуждениях допущена вычислительная ошибка или описка, возможно приведшая к неверному ответу. 0 баллов другие случаи, не соответствующие указанным критериям |
|
|
|
|
Итого 9 |
|
Итоговая контрольная работа (8 класс)
План диагностической работы
|
№ задания |
КЭС (код) |
Раздел программы (содержательная линия) |
Проверяемый планируемый результат |
Уровень сложности |
Тип задания |
Время выполнения (мин) |
Максимальный балл |
|
1 |
1.4.1 |
Числа и дроби |
Находить значение арифметического квадратного корня |
Базовый |
Со свободным, кратким однозначным ответом |
2 |
1 балл |
|
2 |
1.3.5 |
Числа и дроби |
Выполнять действия со степенями с целыми показателями |
Базовый |
Со свободным, кратким однозначным ответом |
2 |
1 балл |
|
3 |
2.4.3 |
Тождественные преобразования |
Выполнять несложные преобразования дробно-рациональных выражений |
Базовый |
Со свободным, кратким однозначным ответом |
3 |
1 балл |
|
4 |
3.1.3 |
Уравнения и неравенства |
Умение решать квадратные уравнения |
Базовый |
Со свободным, кратким однозначным ответом |
2 |
1 балл |
|
5 |
6.1.1 |
Уравнения и неравенства |
Умение находить абсциссу точки по заданной ординате |
Базовый |
Со свободным, кратким однозначным ответом |
2 |
1 балл |
|
6 |
2.3.4 |
Уравнения и неравенства |
Применение теоремы Виета для квадратного уравнения |
Базовый |
Со свободным, кратким однозначным ответом |
1 |
1 балл |
|
7 |
3.1.8 |
Уравнения и неравенства |
Умение решать системы линейных уравнений |
Базовый |
Со свободным, кратким однозначным ответом |
3 |
1 балл |
|
8 |
1.5.5 |
Измерения, приближения, оценка |
Находить пересечение множеств |
Базовый |
Со свободным, кратким однозначным ответом |
2 |
1 балл |
|
9 |
1.5.3 |
Числа и дроби |
Работа с таблицами, определение соотношения между величинами |
Базовый |
Со свободным, кратким однозначным ответом |
3 |
1 балл |
|
10 |
3.1.4 |
Уравнения и неравенства |
Умение находить область допустимых значений переменной |
Базовый |
С выбором верного ответа из нескольких вариантов |
2 |
1 балл |
|
11 |
2.5.1 |
Тождественные преобразования |
Выполнение преобразований с использованием свойств арифметического квадратного корня |
Повышенный |
С выбором верного ответа из нескольких вариантов |
2 |
1 балл |
|
12 |
8.1.2 |
Статистика и теория вероятности |
Умение находить статистические характеристики числового ряда |
Повышенный |
Со свободным, кратким однозначным ответом |
1 |
1 балл |
|
13 |
2.4.3 |
Тождественные преобразования |
Выполнение преобразований дробно-рациональных выражений, с использованием формул сокращенного умножения |
Повышенный |
С развернутым ответом |
5 |
2 балла
|
|
14 |
3.1.7 |
Уравнения и неравенства |
Умение находить точку пересечения графиков функций с помощью уравнения |
Повышенный |
С развернутым ответом |
5 |
2 балла |
|
15 |
3.3.2 |
Текстовые задачи |
Составление уравнение по заданным условиям, решение уравнений |
Повышенный |
С развернутым ответом |
10 |
2 балла
|
|
|
|
|
|
|
|
45 мин |
18 баллов |
Вариант I
1 часть
В каждом задании первой части необходимо записать верный ответ, в отведенном для этого месте. Каждый верный ответ оценивается в один балл.
1.
Вычислите:
![]()
Ответ:_____________________________
2. Найдите значение
дроби:
![]() ,
,
Ответ:_____________________________
3. Сократите дробь ![]() , найдите значение дроби, если
, найдите значение дроби, если ![]() .
.
Ответ:_____________________________
4. Решите
уравнение: ![]() , в ответе укажите наибольший из корней.
, в ответе укажите наибольший из корней.
Ответ:_____________________________
5. График функции ![]() проходит через точку К с ординатой 9.
Найдите абсциссу точки К.
проходит через точку К с ординатой 9.
Найдите абсциссу точки К.
Ответ:_____________________________
6. Найдите
произведение корней уравнения: ![]() .
.
Ответ:_____________________________
7. Пара чисел ![]() является решением системы
является решением системы ![]() . Найдите
. Найдите ![]() .
.
Ответ:_____________________________
8. Укажите наибольшее
целое число, удовлетворяющее условию ![]() , если
, если ![]() .
.
Ответ:_____________________________
9. В таблице представлены данные о количестве населения крупнейших (более 100 тыс. жителей), городов Челябинской области (на 4 декабря 2017г).
|
Город |
Количество жителей |
|
Челябинск |
1202371 |
|
Магнитогорск |
418241 |
|
Златоуст |
167978 |
|
Миасс |
151856 |
|
Копейск |
147573 |
Определите, во сколько раз численность населения Челябинска превышает численность населения Магнитогорска? (Ответ округлите до сотых).
Ответ: ________________________________
10. Определите, какие значения НЕ может
принимать переменная ![]() в выражении:
в выражении: ![]() ?
?
1) ![]()
2) ![]()
3) ![]()
4) ![]()
Ответ: _____________________________________
11. Упростите выражение: ![]()
1) ![]() ;
;
2) ![]() ;
;
3) ![]() ;
;
4) ![]() ;
;
Ответ: _______________________________________
12. На тренировке хоккейной команды «Трактор» девять игроков забили в ворота 19, 12, 17, 18, 14, 20, 23, 17, 21 шайбы соответственно. Найдите медиану полученного ряда чисел.
Ответ: ___________________________________
2 часть
Для записи решений и ответов каждого задания второй части используйте тетрадные листы в клетку. Запишите номер выполняемого задания, затем полное обоснованное решение и ответ. Каждое задание второй части оценивается от нуля до двух баллов.
13. Упростите выражение: ![]()
14. Найдите точки пересечения графиков
функций ![]()
15. Из Златоуста в санаторий «Увильды», расстояние между которыми равно120 км выехал автобус. Через 1 час вслед за ним выехал автомобиль, скорость которого больше скорости автобуса на 20км/ч. Автомобиль прибыл в конечный пункт одновременно с автобусом. Найдите скорость автобуса и автомобиля.
Вариант II
1 часть
В каждом задании первой части необходимо записать верный ответ, в отведенном для этого месте. Каждый верный ответ оценивается в один балл.
1.
Вычислите:
![]()
Ответ: _______________________
2.
Найдите
значение дроби:
![]() ,
,
Ответ: _______________________
3.
Сократите
дробь ![]() , найдите значение дроби, если
, найдите значение дроби, если ![]() .
.
Ответ: _______________________
4.
Решите
уравнение: ![]() , в ответе укажите наибольший из
корней.
, в ответе укажите наибольший из
корней.
Ответ: _______________________
5.
График
функции ![]() проходит через точку M с ординатой 4.
Найдите абсциссу точки M.
проходит через точку M с ординатой 4.
Найдите абсциссу точки M.
Ответ: _______________________
6.
Найдите
сумму корней уравнения: ![]() .
.
Ответ: ________________________
7.
Пара
чисел ![]() является решением системы
является решением системы ![]() . Найдите
. Найдите ![]() .
.
Ответ: ________________________
8.
Укажите
наименьшее целое число, удовлетворяющее условию ![]() , если
, если ![]() .
.
Ответ: ___________________________
9. В таблице представлены данные о количестве населения крупнейших (более 100 тыс. жителей), городов Челябинской области (на 4 декабря 2017г).
|
Город |
Количество жителей |
|
Челябинск |
1202371 |
|
Магнитогорск |
418241 |
|
Златоуст |
167978 |
|
Миасс |
151856 |
|
Копейск |
147573 |
Определите, во сколько раз численность населения Златоуста меньше численности населения Челябинска? (Ответ округлите до сотых). Ответ: ____________________________
10.
Определите,
какие значения НЕ может принимать переменная ![]() в выражении:
в выражении: ![]() ?
?
1)
![]()
2)
![]()
3)
![]()
4)
![]()
Ответ: ______________________________
11.
Упростите
выражение: ![]()
1)
![]() ;
;
2)
![]() ;
;
3)
![]() ;
;
4)
![]() ;
;
Ответ: _______________________________
12. На тренировке хоккейной команды «Трактор» деdять игроков забили в ворота 17, 22, 13, 15, 15, 19, 23, 20, 21 шайбы соответственно. Найдите медиану полученного ряда чисел.
Ответ: ____________________________
2 часть
Для записи решений и ответов каждого задания второй части используйте тетрадные листы в клетку. Запишите номер выполняемого задания, затем полное обоснованное решение и ответ. Каждое задание второй части оценивается от нуля до двух баллов.
13.
Упростите
выражение: ![]()
14.
Найдите
точки пересечения графиков функций ![]()
15. Из Полетаево в Челябинск, расстояние между которыми равно 30 км выехал велосипедист. Через 1 час вслед за ним выехал мотоциклист, скорость которого больше скорости велосипедиста на 40км/ч. Мотоциклист прибыл в конечный пункт одновременно с велосипедистом. Найдите скорость велосипедиста и мотоциклиста.
Планируемые результаты: Проверить уровень достижения результатов по основным темам курса математики 8 класса для обеспечения возможности успешного продолжения образования на базовом уровне.
Распределение заданий по разделам программ(ы)
|
№ п/п |
Раздел программы (содержательная линия) |
Количество заданий базового уровня сложности |
Количество заданий повышенного уровня сложности |
|
1. |
Числа и дроби |
3 |
|
|
2. |
Элементы теории множеств |
1 |
|
|
3. |
Тождественные преобразования |
2 |
1 |
|
4. |
Статистика, вероятность, комбинаторика |
1 |
|
|
5. |
Уравнения и неравенства |
3 |
|
|
6 |
Функции |
2 |
1 |
|
7 |
Текстовые задачи |
|
1 |
|
|
Всего |
12 |
3 |
Инструкция по проверке и оценке работ
|
№ задания |
Планируемый результат |
Правильный ответ |
Критерии оценивания / Максимальный балл |
||
|
Вариант1 |
Вариант2 |
||||
|
1 |
Вычисление арифметического квадратного корня |
10,9 |
|
1 балл |
|
|
2 |
Применение свойств степени с целым показателем |
3 |
2 |
1 балл |
|
|
3 |
Преобразование рациональных дробей |
1,5 |
2,25 |
1 балл |
|
|
4 |
Решение квадратных уравнений |
3 |
4 |
1 балл |
|
|
5 |
Определение принадлежности точки, графику функции |
81 |
16 |
1 балл |
|
|
6 |
Применение теоремы Виета |
|
1 |
1 балл |
|
|
7 |
Решение системы линейных уравнений |
|
9 |
1 балл |
|
|
8 |
Выполнение действий с множествами, пересечение множеств |
|
|
1 балл |
|
|
9 |
Работа с таблицами |
2,87 |
7,16 |
1 балл |
|
|
10 |
Нахождение области допустимых значений переменной |
3 |
3 |
1 балл |
|
|
11 |
Применение свойств арифметического квадратного корня |
3 |
4 |
1 балл |
|
|
12 |
Определение статистических характеристик ряда чисел |
18 |
19 |
1 балл |
|
|
13 |
Преобразование дробно-рациональных выражений |
|
|
2 балла правильно выполнены преобразования, получен верный ответ. 1 балл решение доведено до конца, но допущена ошибка вычислительного характера или описка, с ее учетом дальнейшие шаги выполнены верно. 0 баллов другие случаи, не соответствующие указанным критериям |
|
|
14 |
Пересечение графиков функций, решение уравнения или системы уравнений. |
|
|
2 балла верно и обоснованно найдены точки пересечения графиков. 1 балл при верных рассуждениях допущена вычислительная ошибка, или описка, возможно приведшая к неверному ответу. 0 баллов другие случаи, не соответствующие указанным критериям |
|
|
15 |
Решение текстовых задач с помощью уравнения |
40км/ч; 60км/ч. |
20км/ч; 60км/ч. |
2 балла получен верный обоснованный ответ. 1 балл при верных рассуждениях допущена вычислительная ошибка, возможно приведшая к неверному ответу. 0 баллов другие случаи, не соответствующие указанным критериям |
|
Геометрия 8 класс. Контрольная работа № 1 «Четырехугольники»
План контрольной работы
|
№ задания |
КЭС (код) |
Раздел программы (содержательная линия) |
Проверяемый планируемый результат |
Уровень сложности |
Тип задания |
Время выполнения (мин) |
Максимальный балл |
|
1 |
7.3.1 |
Измерения и вычисления. Свойства параллелограмма
|
Оперировать на базовом уровне понятиями геометрических фигур (параллелограмм); применять для решения задач геометрические факты, если условия их применения заданы в явной форме |
Базовый |
Со свободным, кратким однозначным ответом |
5 |
1 балл |
|
2 |
7.3.1 |
Измерения и вычисления. Свойства параллелограмма
|
Оперировать на базовом уровне понятиями геометрических фигур (параллелограмм); применять для решения задач геометрические факты, если условия их применения заданы в явной форме |
Базовый |
Со свободным, кратким однозначным ответом |
5 |
1 балл |
|
3 |
7.3.2 |
Измерения и вычисления. Свойства прямоугольника
|
Применять для решения задач геометрические факты, если условия их применения заданы в явной форме |
Базовый |
Со свободным, кратким однозначным ответом |
5 |
1 балл |
|
4 |
7.3.2 |
Измерения и вычисления. Свойства ромба
|
Применять для решения задач геометрические факты, если условия их применения заданы в явной форме |
Базовый |
Со свободным, кратким однозначным ответом |
5 |
1 балл |
|
5 |
7.3.3 |
Измерения и вычисления. Свойства трапеции
|
Оперировать на базовом уровне понятиями геометрических фигур (трапеция); применять для решения задач геометрические факты, если условия их применения заданы в явной форме |
Базовый |
Со свободным, кратким однозначным ответом |
5 |
1 балл |
|
6 |
7.3.1 |
Измерения и вычисления. Свойства параллелограмма |
Геометрические факты для решения задач, в том числе, предполагающих несколько шагов решения |
Повышенный |
С развернутым ответом |
7 |
2 балла |
|
7 |
7.3.3 |
Измерения и вычисления. Свойства трапеции
|
Геометрические факты для решения задач, в том числе, предполагающих несколько шагов решения |
Повышенный |
С развернутым ответом |
8 |
2 балла |
|
|
|
|
|
|
|
40 мин |
9 баллов |
Вариант 1
Инструкция по выполнению работы
Контрольная работа состоит из двух частей и включает в себя 7 заданий: 5 заданий в первой части и 2 задания во второй части. На выполнение работы отводится 45 минут. В первой части работы запишите ответы к заданиям в поле ответа в тексте работы. При выполнении заданий можно пользоваться черновиком. Записи в черновике не учитываются при оценивании работы.
Решения заданий части 2 и ответы к ним запишите на отдельном листе или бланке.
Задания можно выполнять в любом порядке.
Текст задания переписывать не надо, необходимо только указать его номер.
Баллы, полученные Вами за выполненные задания, суммируются.
Постарайтесь выполнить как можно больше заданий и набрать наибольшее количество баллов.
|
1. Величины двух углов параллелограмма пропорциональны числам 2 и 8. Найдите больший угол параллелограмма.
Ответ:______________________
5. Найдите периметр параллелограмма АВСМ, если биссектриса острого угла С делит сторону АМ на отрезки АК=7 см, КМ=9 см.
Ответ:______________________
6. Угол между диагоналями прямоугольника равен 600. Меньшая сторона прямоугольника равна
4,5 см. Найдите длину диагонали прямоугольника.
Ответ:______________________
4. Диагонали ромба образуют со стороной ромба углы, величины которых пропорциональны числам 6 и 3. Найдите больший угол ромба.
Ответ:______________________
5. Найдите высоту равнобедренной трапеции, основания которой равны 8 см и 10 см, а острый угол равен 450.
Ответ:______________________
Часть 2
|
6. Биссектрисы углов параллелограмма, прилежащих к одной стороне, делят противолежащую сторону параллелограмма на три равных отрезка. Найдите смежные стороны параллелограмма, если его периметр равен 120 см и биссектрисы не пересекаются.
7.
В ромбе АВСМ биссектриса угла ВСА пересекает сторону ВС в точке Р. Найдите
острый угол ромба, если ![]() .
.
Вариант 2
Инструкция по выполнению работы
Контрольная работа состоит из двух частей и включает в себя 7 заданий: 5 заданий в первой части и 2 задания во второй части. На выполнение работы отводится 45 минут. В первой части работы запишите ответы к заданиям в поле ответа в тексте работы. При выполнении заданий можно пользоваться черновиком. Записи в черновике не учитываются при оценивании работы.
Решения заданий части 2 и ответы к ним запишите на отдельном листе или бланке.
Задания можно выполнять в любом порядке.
Текст задания переписывать не надо, необходимо только указать его номер.
Баллы, полученные Вами за выполненные задания, суммируются.
Постарайтесь выполнить как можно больше заданий и набрать наибольшее количество баллов.
|
1. Величины двух углов параллелограмма пропорциональны числам 7 и 11. Найдите больший угол параллелограмма.
Ответ:______________________
2. Найдите периметр параллелограмма АВСМ, если биссектриса тупого угла В параллелограмма делит сторону АМ на отрезки АК=8 см, КМ=15 см.
Ответ:______________________
3. Угол между диагоналями прямоугольника равен 600. Меньшая сторона прямоугольника равна 12,5 см. Найдите длину диагонали прямоугольника.
Ответ:______________________
4. Диагонали ромба образуют со стороной ромба углы, величины которых пропорциональны числам 2 и 7. Найдите меньший угол ромба.
Ответ:______________________
5. Найдите высоту равнобедренной трапеции, основания которой равны 3 см и 12 см, а острый угол равен 450.
Ответ:______________________
Часть 2
|
6. Биссектрисы углов параллелограмма, прилежащих к одной стороне, делят противолежащую сторону параллелограмма на три равных отрезка. Найдите смежные стороны параллелограмма, если его периметр равен 88 см и биссектрисы не пересекаются.
7.
В
ромбе АВСМ биссектриса угла САВ пересекает сторону ВС в точке Р. Найдите острый
угол ромба, если ![]() .
.
Инструкция по проверке и оценке работ
|
№ задания |
Планируемый результат |
Правильный ответ |
Критерии оценивания / Максимальный балл |
|
|
Вариант1 |
Вариант2 |
|||
|
1 |
Решение задач на применение свойства углов параллелограмма |
144 |
110 |
1 балл |
|
2 |
Решение задач на свойство сторон параллелограмма |
50 см |
62 см |
1 балл |
|
3 |
Решение задач на свойство диагоналей прямоугольника |
9 см |
25 см |
1 балл |
|
4 |
Решение задач на свойства ромба |
1200 |
400 |
1 балл |
|
5 |
Решение задач на нахождение элементов трапеции |
1 см |
4,5 см |
1 балл |
|
6 |
Решение задачи на применение свойств параллелограмма |
15см, 45 см |
11 см |
2 балла - ход решения верный, все его шаги выполнены правильно, получен верный ответ 1 балл - ход решения верный, все его шаги выполнены правильно, но даны неполные объяснения или допущена одна вычислительная ошибка |
|
7 |
Решение задач на применение свойства углов трапеции |
17 см |
13 см |
2 балла - ход решения верный, все его шаги выполнены правильно, получен верный ответ 1 балл - ход решения верный, все его шаги выполнены правильно, но даны неполные объяснения или допущена одна вычислительная ошибка |
Контрольная работа № 2 «Площади»
План контрольной работы
|
№ задания |
КЭС (код) |
Раздел программы (содержательная линия) |
Проверяемый планируемый результат |
Уровень сложности |
Тип задания |
Время выполнения (мин) |
Максимальный балл |
|
1 |
7.5.5 |
Отношения. Свойства площадей
|
Применять формулы периметра, площади многоугольников, при вычислениях, когда все данные имеются в условии |
Базовый |
Со свободным, кратким однозначным ответом |
5 |
1 балл |
|
2 |
7.5.4 |
Измерения и вычисления. Площадь ромба
|
Применять формулы периметра, площади многоугольников (параллелограммов, треугольников, трапеций), |
Базовый |
Со свободным, кратким однозначным ответом |
5 |
1 балл |
|
3 |
7.5.4 |
Измерения и вычисления. Площадь параллелограмма
|
Применять формулы периметра, площади многоугольников (параллелограммов, треугольников, трапеций), |
Базовый |
Со свободным, кратким однозначным ответом |
5 |
1 балл |
|
4 |
7.2.3 |
Измерения и вычисления. Площадь прямоугольного треугольника. Теорема Пифагора
|
Применять формулы периметра, площади многоугольников (параллелограммов, треугольников, трапеций), |
Базовый |
Со свободным, кратким однозначным ответом |
5 |
1 балл |
|
5 |
7.2.3 |
Измерения и вычисления. Площадь треугольника. Теорема Пифагора
|
Оперировать на базовом уровне понятиями геометрических фигур (трапеция); применять для решения задач геометрические факты, если условия их применения заданы в явной форме |
Базовый |
Со свободным, кратким однозначным ответом |
5 |
1 балл |
|
6 |
7.5.6 |
Измерения и вычисления. Площадь трапеции
|
Геометрические факты для решения задач, в том числе, предполагающих несколько шагов решения |
Повышенный |
С развернутым ответом |
7 |
2 балла |
|
7 |
7.5.5 |
Измерения и вычисления. Площадь параллелограмма и трапеции. Свойства площадей
|
Геометрические факты для решения задач, в том числе, предполагающих несколько шагов решения |
Повышенный |
С развернутым ответом |
8 |
2 балла |
|
|
|
|
|
|
|
40 мин |
9 баллов |
Вариант I
1 часть
В каждом задании первой части необходимо записать верный ответ, в отведенном для этого месте. Каждый верный ответ оценивается в один балл.
1. Во сколько раз увеличится площадь квадрата, если его сторону увеличить в 3 раза?
Ответ:______________________
7. Найдите площадь ромба, если его диагонали равны 18 см и 6 см.
Ответ:______________________
3. Стороны параллелограмма равны 12 см и 15 см. Его меньшая высота 5 см. Найдите другую высоту.
Ответ:______________________
4. Найдите площадь прямоугольного треугольника, катеты которого пропорциональны числам 6 и 8, а гипотенуза равна 30.
Ответ:______________________
5. Найдите площадь равнобедренного треугольника, если его боковая сторона равна 13 см, а основание равно 24 см.
Ответ:______________________
II часть
Для записи решений и ответов каждого задания второй части используйте тетрадные листы в клетку. Запишите номер выполняемого задания, затем полное обоснованное решение и ответ. Каждое задание второй части оценивается от нуля до двух баллов.
6. Длины высоты и основания трапеции пропорциональны числам 4, 6, 9. Найдите меньшее основание трапеции, если ее площадь равна 270 см2.
7. На стороне ВС параллелограмма ABCD отметили точку М. Площадь треугольника АМD равна 18 см2. Найдите площадь параллелограмма ABCD.
Вариант II
1 часть
В каждом задании первой части необходимо записать верный ответ, в отведенном для этого месте. Каждый верный ответ оценивается в один балл.
1. Во сколько раз уменьшится площадь квадрата, если его сторону уменьшить в 5 раз?
Ответ:______________________
2. Найдите площадь ромба, если его диагонали равны 24 см и 8 см.
Ответ:______________________
3. Стороны параллелограмма равны 18 см и 15 см. Его большая высота 9 см. Найдите другую высоту.
Ответ:______________________
4. Найдите площадь прямоугольного треугольника, катеты которого пропорциональны числам 5 и 12, а гипотенуза равна 39.
Ответ:______________________
5. Найдите площадь равнобедренного треугольника, если его боковая сторона равна 17 см, а основание равно 16 см.
Ответ:______________________
II часть
Для записи решений и ответов каждого задания второй части используйте тетрадные листы в клетку. Запишите номер выполняемого задания, затем полное обоснованное решение и ответ. Каждое задание второй части оценивается от нуля до двух баллов.
6. Длины высоты и основания трапеции пропорциональны числам 4, 6, 5. Найдите меньшее основание трапеции, если ее площадь равна 176 см2.
7. На стороне ВС параллелограмма ABCD отметили точку М. Площадь треугольника АМD равна 25 см2. Найдите площадь параллелограмма ABCD.
Инструкция по проверке и оценке работ
|
№ задания |
Планируемый результат |
Правильный ответ |
Критерии оценивания / Максимальный балл |
|
|
Вариант1 |
Вариант2 |
|||
|
1 |
Решение задач на применение свойства углов параллелограмма |
9 |
25 |
1 балл |
|
2 |
Решение задач на свойство сторон параллелограмма |
54 см2 |
96 см2 |
1 балл |
|
3 |
Решение задач на свойство диагоналей прямоугольника |
6,25 см |
7,5 см |
1 балл |
|
4 |
Решение задач на свойства ромба |
216 |
270 |
1 балл |
|
5 |
Решение задач на нахождение элементов трапеции |
60 см2 |
120 см2 |
1 балл |
|
6 |
Решение задачи на применение свойств параллелограмма |
18 см |
|
2 балла - ход решения верный, все его шаги выполнены правильно, получен верный ответ 1 балл - ход решения верный, все его шаги выполнены правильно, но даны неполные объяснения или допущена одна вычислительная ошибка |
|
7 |
Решение задач на применение свойства углов трапеции |
36 см2 |
50 см2 |
2 балла - ход решения верный, все его шаги выполнены правильно, получен верный ответ 1 балл - ход решения верный, все его шаги выполнены правильно, но даны неполные объяснения или допущена одна вычислительная ошибка |
Контрольная работа № 3 «Подобные треугольники»
План контрольной работы
|
№ задания |
КЭС (код) |
Раздел программы (содержательная линия) |
Проверяемый планируемый результат |
Уровень сложности |
Тип задания |
Время выполнения (мин) |
Максимальный балл |
|
1 |
7.2.9 |
Геометрические фигуры. Средняя линия треугольника
|
Оперировать на базовом уровне понятиями: подобие фигур, подобные фигуры, подобные треугольники |
Базовый |
Со свободным, кратким однозначным ответом |
5 |
1 балл |
|
2 |
7.2.11 |
Измерения и вычисления. Пропорциональные отрезки в прямоугольном треугольнике
|
Оперировать на базовом уровне понятиями: подобие фигур, подобные фигуры, подобные треугольники, находить неизвестные элементы в подобных треугольниках |
Базовый |
Со свободным, кратким однозначным ответом |
5 |
1 балл |
|
3 |
7.2.11 |
Измерения и вычисления. Определение тригонометрических функций
|
Применять для решения задач геометрические факты, если условия их применения заданы в явной форме |
Базовый |
Со свободным, кратким однозначным ответом |
5 |
1 балл |
|
4 |
7.2.11 |
Измерения и вычисления. Определение тригонометрических функций
|
Применять для решения задач геометрические факты, если условия их применения заданы в явной форме |
Базовый |
Со свободным, кратким однозначным ответом |
5 |
1 балл |
|
5 |
7.2.11 |
Измерения и вычисления. Определение тригонометрических функций
|
применять для решения практических задач геометрические факты, если условия их применения заданы в явной форме |
Базовый |
Со свободным, кратким однозначным ответом |
5 |
1 балл |
|
6 |
7.2.11 |
Измерения и вычисления. Определение тригонометрических функций
|
геометрические факты для решения задач, в том числе, предполагающих несколько шагов решения |
Повышенный |
С развернутым ответом |
7 |
2 балла |
|
7 |
7.2.9 |
Отношения. Свойство средней линии треугольника
|
геометрические факты для решения задач, в том числе, предполагающих несколько шагов решения |
Повышенный |
С развернутым ответом |
8 |
2 балла |
|
|
|
|
|
|
|
40 мин |
9 баллов |
Вариант 1
Инструкция по выполнению работы
Контрольная работа состоит из двух частей и включает в себя 7 заданий: 5 заданий в первой части и 2 задания во второй части. На выполнение работы отводится 45 минут. В первой части работы запишите ответы к заданиям в поле ответа в тексте работы. При выполнении заданий можно пользоваться черновиком. Записи в черновике не учитываются при оценивании работы.
Решения заданий части 2 и ответы к ним запишите на отдельном листе или бланке.
Задания можно выполнять в любом порядке.
Текст задания переписывать не надо, необходимо только указать его номер.
Баллы, полученные Вами за выполненные задания, суммируются.
Постарайтесь выполнить как можно больше заданий и набрать наибольшее количество баллов.
|
2. В прямоугольнике диагональ равна 36 см. Чему равен периметр четырехугольника, вершинами которого являются середины сторон прямоугольника?
Ответ:______________________
3. В прямоугольном треугольнике АВС с прямым углом С проведена высота CD, которая делит гипотенузу АВ на отрезки AD и DB. Найдите высоту CD, если АВ=26 см, AD=8 см.
Ответ:______________________
4. В прямоугольном треугольнике АВС с прямым углом С катеты равны АС=6 см, ВС=8 см. Найдите синус угла А.
Ответ:______________________
5. Синус острого угла в прямоугольном треугольнике равен 0,8. Найдите косинус этого угла.
Ответ:______________________
6. Найдите расстояние от наблюдателя до главного здания ЮУрГУ, если высота здания 86 м, а угол, под которым видно здание равен 30˚. В ответе укажите приближенное значение, равное целому числу метров.
Ответ:______________________
Часть 2
|
7. Через точку М, взятую на медиане АD треугольника ABC, и вершину В проведена прямая, пересекающая сторону АС в точке К. Найдите отношение АК : КС, если M - середина отрезка AD.
8. В равностороннем треугольнике ABC точки M, N, K — середины сторон АВ, ВС, СА соответственно. Докажите, что треугольник MNK — равносторонний.
Вариант 2
Инструкция по выполнению работы
Контрольная работа состоит из двух частей и включает в себя 7 заданий: 5 заданий в первой части и 2 задания во второй части. На выполнение работы отводится 45 минут. В первой части работы запишите ответы к заданиям в поле ответа в тексте работы. При выполнении заданий можно пользоваться черновиком. Записи в черновике не учитываются при оценивании работы.
Решения заданий части 2 и ответы к ним запишите на отдельном листе или бланке.
Задания можно выполнять в любом порядке.
Текст задания переписывать не надо, необходимо только указать его номер.
Баллы, полученные Вами за выполненные задания, суммируются.
Постарайтесь выполнить как можно больше заданий и набрать наибольшее количество баллов.
|
1. В равнобедренной трапеции диагональ равна 18 см. Найдите периметр четырехугольника, вершинами которого являются середины сторон трапеции.
Ответ:______________________
2. В прямоугольном треугольнике АВС с прямым углом С проведена высота CD, которая делит гипотенузу АВ на отрезки AD и DB. Найдите катет АС, если АВ=16 см, ВD=7 см.
Ответ:______________________
3. В прямоугольном треугольнике АВС с прямым углом С катеты равны АС=6 см, ВС=8 см. Найдите синус угла В.
Ответ:______________________
4. Синус острого угла в прямоугольном треугольнике равен 0,6. Найдите косинус этого угла.
Ответ:______________________
5. Найдите расстояние от наблюдателя до главного здания ЮУрГУ, если высота здания 86 м, а угол, под которым видно здание равен 60˚. В ответе укажите приближенное значение, равное целому числу метров.
Ответ:______________________
Часть 2
|
6. Через вершину В треугольника АВС проведена прямая ВМ, параллельная АС. Из вершины А проведен луч, пересекающий прямую ВМ в точке D, сторону ВС в точке N, медиану BH в точке К. В каком отношении точка К делит медиану ВН, если BN : NC=1 : 2.
7. В равностороннем треугольнике ABC точки M, N, K — середины сторон АВ, ВС, СА соответственно. Докажите, что ВMKN — ромб.
Инструкция по проверке и оценке работ
|
№ задания |
Планируемый результат |
Правильный ответ |
Критерии оценивания / Максимальный балл |
|
|
Вариант1 |
Вариант2 |
|||
|
1 |
Решение задач на применение подобных треугольников. Средняя линия треугольника |
72см |
36 см |
1 балл |
|
2 |
Решение задач на применение подобных треугольников. Пропорциональные отрезки в прямоугольном треугольнике |
12 см |
12 см |
1 балл |
|
3 |
Решение треугольников |
0,8 |
0,6 |
1 балл |
|
4 |
Решение треугольников |
0,6 |
0,8 |
1 балл |
|
5 |
Решение треугольников |
146 м |
51 м |
1 балл |
|
6 |
Решение треугольников |
12 |
16 |
2 балла - ход решения верный, все его шаги выполнены правильно, получен верный ответ 1 балл - ход решения верный, все его шаги выполнены правильно, но даны неполные объяснения или допущена одна вычислительная ошибка |
|
7 |
Решение задач на применение свойств средней линии треугольника |
|
|
2 балла - доказательство верное, все шаги обоснованы, 1 балл - доказательство в целом верное, но содержит неточности |
Контрольная работа № 4 «Соотношения между сторонами и углами прямоугольного треугольника»
План контрольной работы
|
№ задания |
КЭС (код) |
Раздел программы (содержательная линия) |
Проверяемый планируемый результат |
Уровень сложности |
Тип задания |
Время выполнения (мин) |
Максимальный балл |
|
1 |
7.2.9 |
Геометрические фигуры
|
Оперировать на базовом уровне понятиями: подобие фигур, подобные фигуры, подобные треугольники |
Базовый |
Со свободным, кратким однозначным ответом |
5 |
1 балл |
|
2 |
7.2.9 |
Измерения и вычисления. Подобные треугольники
|
Оперировать на базовом уровне понятиями: подобие фигур, подобные фигуры, подобные треугольники, находить неизвестные элементы в подобных треугольниках |
Базовый |
Со свободным, кратким однозначным ответом |
5 |
1 балл |
|
3 |
7.2.9 |
Измерения и вычисления. Отношение периметров подобных треугольников
|
Применять для решения задач геометрические факты, если условия их применения заданы в явной форме |
Базовый |
Со свободным, кратким однозначным ответом |
5 |
1 балл |
|
4 |
7.2.9 |
Измерения и вычисления. Отношения площадей подобных треугольников
|
Применять для решения задач геометрические факты, если условия их применения заданы в явной форме |
Базовый |
Со свободным, кратким однозначным ответом |
5 |
1 балл |
|
5 |
7.2.1 |
Измерения и вычисления. Свойство биссектрисы треугольника
|
Применять для решения задач геометрические факты, если условия их применения заданы в явной форме |
Базовый |
Со свободным, кратким однозначным ответом |
5 |
1 балл |
|
6 |
7.2.9 |
Измерения и вычисления. Свойства площадей подобных треугольников |
Геометрические факты для решения задач, в том числе, предполагающих несколько шагов решения |
Повышенный |
С развернутым ответом |
7 |
2 балла |
|
7 |
7.2.9 |
Отношения. Признаки и свойства подобных треугольников
|
Геометрические факты для решения задач, в том числе, предполагающих несколько шагов решения |
Повышенный |
С развернутым ответом |
8 |
2 балла |
|
|
|
|
|
|
|
40 мин |
9 баллов |
Вариант 1
Инструкция по выполнению работы
Контрольная работа состоит из двух частей и включает в себя 7 заданий: 5 заданий в первой части и 2 задания во второй части. На выполнение работы отводится 45 минут. В первой части работы запишите ответы к заданиям в поле ответа в тексте работы. При выполнении заданий можно пользоваться черновиком. Записи в черновике не учитываются при оценивании работы.
Решения заданий части 2 и ответы к ним запишите на отдельном листе или бланке.
Задания можно выполнять в любом порядке.
Текст задания переписывать не надо, необходимо только указать его номер.
Баллы, полученные Вами за выполненные задания, суммируются.
Постарайтесь выполнить как можно больше заданий и набрать наибольшее количество баллов.
|
6. На рисунке даны два подобных прямоугольных треугольника. Какая запись пропорциональности всех пар сходственных сторон будет верной?
1) ![]()
![]()
2) ![]()
3) ![]()
4) ![]()
Ответ:______________________
7. В треугольнике АВС АВ=10, ВС=8. Отрезок NKпараллелен АВ, причем точка Nлежит на стороне ВС, точка К лежит на стороне АС, CN=4. Найдите NK.
Ответ:______________________
8.
Треугольники
ВОС и РМК подобны. ![]() . Найдите
периметр треугольника ВОС, если периметр треугольника РМК равен 34 см.
. Найдите
периметр треугольника ВОС, если периметр треугольника РМК равен 34 см.
Ответ:______________________
9. Треугольники MNK и FTC подобны. Площадь треугольника FTCсоставляет 0,36 площади треугольника MNK. Найдите коэффициент подобия этих треугольников.
Ответ:______________________
10. В треугольнике АВС со стороной АС=15 см проведена биссектриса АК. Точка К делит сторону ВС на отрезки ВК=7 см, КС=6 см. Найдите сторону АВ.
Ответ:______________________
Часть 2
|
6. В треугольнике АВС на стороне АВ взяли точку М, на стороне ВС взяли точку Р так, что АМ : МВ = СР : РВ = 3 : 1. Во сколько раз площадь четырехугольника АМРС больше меньше площади треугольника АВС?
7.
В треугольнике АВС на стороне АС выбрали точку К так, что ![]() . Докажите, что
. Докажите, что ![]() .
.
Вариант 2
Инструкция по выполнению работы
Контрольная работа состоит из двух частей и включает в себя 7 заданий: 5 заданий в первой части и 2 задания во второй части. На выполнение работы отводится 45 минут. В первой части работы запишите ответы к заданиям в поле ответа в тексте работы. При выполнении заданий можно пользоваться черновиком. Записи в черновике не учитываются при оценивании работы.
Решения заданий части 2 и ответы к ним запишите на отдельном листе или бланке.
Задания можно выполнять в любом порядке.
Текст задания переписывать не надо, необходимо только указать его номер.
Баллы, полученные Вами за выполненные задания, суммируются.
Постарайтесь выполнить как можно больше заданий и набрать наибольшее количество баллов.
|
1. На рисунке даны
два подобных треугольника АОВ и CODи ![]() . Какая запись пропорциональности
всех пар сходственных сторон будет верной?
. Какая запись пропорциональности
всех пар сходственных сторон будет верной?
1) ![]()
![]()
2) ![]()
3) ![]()
4) ![]()
Ответ:______________________
2. В треугольнике АВС АВ=8, ВС=10. Отрезок NKпараллелен ВС, причем точка Nлежит на стороне АВ, точка К лежит на стороне АС, ВN=2. Найдите NK.
Ответ:______________________
3.
Треугольники
ВОС и РМК подобны. ![]() . Найдите
периметр треугольника ВОС, если периметр треугольника РМК равен 12 см.
. Найдите
периметр треугольника ВОС, если периметр треугольника РМК равен 12 см.
Ответ:______________________
4. Треугольники MNK и FTC подобны. Площадь треугольника FTC составляет 0,64 площади треугольника MNK. Найдите коэффициент подобия этих треугольников.
Ответ:______________________
5. В треугольнике АВС со сторонами АС=17 см, ВС=10 см, АВ=15 см проведена биссектриса ВК. Точка К делит сторону АС на отрезки. Найдите меньший из них.
Ответ:______________________
Часть 2
|
6. В треугольнике АВС на стороне АВ взяли точку М, на стороне ВС взяли точку Р так, что АМ : МВ = СР : РВ = 4 : 1. Во сколько раз площадь четырехугольника АМРС больше площади треугольника РМВ?
7.
В
треугольнике КМР на стороне КР выбрали точку В так, что ![]() . Докажите, что
. Докажите, что ![]() .
.
Инструкция по проверке и оценке работ
|
№ задания |
Планируемый результат |
Правильный ответ |
Критерии оценивания / Максимальный балл |
|
|
Вариант1 |
Вариант2 |
|||
|
1 |
Решение задач на определение подобных треугольников |
3 |
4 |
1 балл |
|
2 |
Решение задач на нахождение элементов подобных треугольников |
5 |
7,5 |
1 балл |
|
3 |
Решение задач на отношение периметров подобных треугольников |
40,8 см |
16,8 см |
1 балл |
|
4 |
Решение задач на нахождение площадей подобных треугольников |
0,6 |
0,8 |
1 балл |
|
5 |
Решение задач на применение свойств биссектрисы угла |
17,5 см |
6,8 см |
1 балл |
|
6 |
Решение задачи на применение признаков и свойств подобных треугольников |
15 |
24 |
2 балла - ход решения верный, все его шаги выполнены правильно, получен верный ответ 1 балл - ход решения верный, все его шаги выполнены правильно, но даны неполные объяснения или допущена одна вычислительная ошибка |
|
7 |
Решение задач на применение свойств и признаков подобных треугольников |
|
|
2 балла - доказательство верное, все шаги обоснованы, 1 балл - доказательство в целом верное, но содержит неточности |
Контрольная работа № 5 «Окружность»
План контрольной работы
|
№ задания |
КЭС (код) |
Раздел программы (содержательная линия) |
Проверяемый планируемый результат |
Уровень сложности |
Тип задания |
Время выполнения (мин) |
Максимальный балл |
|
1 |
7.4.5 |
Измерения и вычисления. Вписанный в окружность прямоугольный треугольник
|
Решать задачи на нахождение геометрических величин по образцам или алгоритмам. |
Базовый |
Со свободным, кратким однозначным ответом |
5 |
1 балл |
|
2 |
7.4.5 |
Измерения и вычисления. Свойство отрезков хорд
|
Решать задачи на нахождение геометрических величин по образцам или алгоритмам. |
Базовый |
Со свободным, кратким однозначным ответом |
5 |
1 балл |
|
3 |
7.4.6 |
Измерения и вычисления. Описанный четырехугольник
|
Применять для решения задач геометрические факты, если условия их применения заданы в явной форме |
Базовый |
Со свободным, кратким однозначным ответом |
5 |
1 балл |
|
4 |
7.2.9 |
Измерения и вычисления. Свойства отрезков касательных
|
Применять для решения задач геометрические факты, если условия их применения заданы в явной форме |
Базовый |
Со свободным, кратким однозначным ответом |
5 |
1 балл |
|
5 |
7.4.3 |
Измерения и вычисления. Свойство касательной к окружности
|
Применять для решения задач геометрические факты, если условия их применения заданы в явной форме |
Базовый |
Со свободным, кратким однозначным ответом |
5 |
1 балл |
|
6 |
7.4.1 |
Измерения и вычисления. Вписанный угол
|
Геометрические факты для решения задач, в том числе, предполагающих несколько шагов решения |
Повышенный |
С развернутым ответом |
7 |
2 балла |
|
7 |
7.4.3 |
Отношения. Свойства отрезков касательных
|
Геометрические факты для решения задач, в том числе, предполагающих несколько шагов решения |
Повышенный |
С развернутым ответом |
8 |
2 балла |
|
|
|
|
|
|
|
40 мин |
9 баллов |
Вариант I
1 часть
В каждом задании первой части необходимо записать верный ответ, в отведенном для этого месте. Каждый верный ответ оценивается в один балл.
1. Прямоугольный треугольник с катетами 16 см и 12 см вписан в окружность. Найдите радиус этой окружности.
Ответ:______________________
2. Две хорды окружности АВ и МК пересекаются в точке Р. АР=8 см, РВ=9 см, Отрезок МР в 2 раза больше отрезка РК. Найдите длину отрезка МР.
Ответ:______________________
3. В четырехугольник АВСD вписана окружность. Найдите его периметр, если АВ=47 см, CD=48 см.
Ответ:______________________
4. Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, длины которых 23 и 9, считая от вершины, противолежащей основанию. Найдите периметр треугольника.
Ответ:______________________
5. К окружности с центром О и радиусом 9 см проведена касательная АВ (А – точка касания). Найдите длину отрезка ВО, если АВ=12 см.
Ответ:______________________
II часть
Для записи решений и ответов каждого задания второй части используйте тетрадные листы в клетку. Запишите номер выполняемого задания, затем полное обоснованное решение и ответ. Каждое задание второй части оценивается от нуля до двух баллов
6. Четырехугольник АВСD вписан в окружность. Угол АВD равен 750, угол САD равен 350. Найдите угол АВС.
7. В треугольник АВС вписана окружность. К этой окружности провели три касательные. Периметры отсеченных треугольников равны 10 см, 6 см, 38 см. Найдите периметр треугольника АВС.
Вариант II
1 часть
В каждом задании первой части необходимо записать верный ответ, в отведенном для этого месте. Каждый верный ответ оценивается в один балл.
1. Прямоугольный треугольник с катетом 16 см вписан в окружность радиуса 10 см. Найдите второй катет треугольника.
Ответ:______________________
2. Две хорды окружности АВ и МК пересекаются в точке Р. АР=2 см, РВ=16 см, Отрезок МР в 2 раза больше отрезка РК. Найдите длину хорды МК.
Ответ:______________________
3. В четырехугольник АВСD вписана окружность. Найдите его периметр, если АВ=15 см, CD=18 см.
Ответ:______________________
4. Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, длины которых 18 и 3, считая от вершины, противолежащей основанию. Найдите периметр треугольника.
Ответ:______________________
5. К окружности с центром О и радиусом 12 см проведена касательная АВ (А – точка касания). Найдите длину отрезка АВ, если ОВ=15 см.
Ответ:______________________
II часть
Для записи решений и ответов каждого задания второй части используйте тетрадные листы в клетку. Запишите номер выполняемого задания, затем полное обоснованное решение и ответ. Каждое задание второй части оценивается от нуля до двух баллов
6. Четырехугольник АВСD вписан в окружность. Угол АСD равен 720, угол АDВ равен 480. Найдите угол ВАD.
7. В треугольник АВС вписана окружность. К этой окружности провели три касательные. Периметры отсеченных треугольников равны 15 см, 12 см, 8 см. Найдите периметр треугольника АВС.
Инструкция по проверке и оценке работ
|
№ задания |
Планируемый результат |
Правильный ответ |
Критерии оценивания / Максимальный балл |
|
|
Вариант1 |
Вариант2 |
|||
|
1 |
Решение задач на свойства вписанного треугольника |
10 см |
12 см |
1 балл |
|
2 |
Решение задач на свойство хорд |
12 см |
12 см |
1 балл |
|
3 |
Решение задач на свойство описанного четырехугольника |
190 см |
66 см |
1 балл |
|
4 |
Решение задач на свойство отрезков касательных |
82 |
48 |
1 балл |
|
5 |
Решение задач на свойство касательной |
15 см |
9 см |
1 балл |
|
6 |
Решение задач на свойство вписанных углов |
1100 |
600 |
|
|
7 |
Решение задач на свойство отрезков касательных |
54 см |
35 см |
2 балла - ход решения верный, все его шаги выполнены правильно, получен верный ответ 1 балл - ход решения верный, все его шаги выполнены правильно, но даны неполные объяснения или допущена одна вычислительная ошибка |
Алгебра 9 класс. Диагностическая работа (входная)
План диагностической работы
|
№ задания |
КЭС (код) |
Раздел программы (содержательная линия) |
Проверяемый планируемый результат |
Уровень сложности |
Тип задания |
Время выполнения (мин) |
Максимальный балл |
|
1 |
1.4.1 |
Числа и дроби |
Находить значение арифметического квадратного корня |
Базовый |
Со свободным, кратким однозначным ответом |
2 |
1 балл |
|
2 |
1.3.5 |
Числа и дроби |
Выполнять действия со степенями с целыми показателями |
Базовый |
Со свободным, кратким однозначным ответом |
2 |
1 балл |
|
3 |
2.4.3 |
Тождественные преобразования |
Выполнять несложные преобразования дробно-рациональных выражений |
Базовый |
Со свободным, кратким однозначным ответом |
3 |
1 балл |
|
4 |
3.1.3 |
Уравнения и неравенства |
Умение решать квадратные уравнения |
Базовый |
Со свободным, кратким однозначным ответом |
2 |
1 балл |
|
5 |
6.1.1 |
Уравнения и неравенства |
Умение находить абсциссу точки по заданной ординате |
Базовый |
Со свободным, кратким однозначным ответом |
2 |
1 балл |
|
6 |
2.3.4 |
Уравнения и неравенства |
Применение теоремы Виета для квадратного уравнения |
Базовый |
Со свободным, кратким однозначным ответом |
1 |
1 балл |
|
7 |
3.1.8 |
Уравнения и неравенства |
Умение решать системы линейных уравнений |
Базовый |
Со свободным, кратким однозначным ответом |
3 |
1 балл |
|
8 |
1.5.5 |
Измерения, приближения, оценка |
Находить пересечение множеств |
Базовый |
Со свободным, кратким однозначным ответом |
2 |
1 балл |
|
9 |
1.5.3 |
Числа и дроби |
Работа с таблицами, определение соотношения между величинами |
Базовый |
Со свободным, кратким однозначным ответом |
3 |
1 балл |
|
10 |
3.1.4 |
Уравнения и неравенства |
Умение находить область допустимых значений переменной |
Базовый |
С выбором верного ответа из нескольких вариантов |
2 |
1 балл |
|
11 |
2.5.1 |
Тождественные преобразования |
Выполнение преобразований с использованием свойств арифметического квадратного корня |
Повышенный |
С выбором верного ответа из нескольких вариантов |
2 |
1 балл |
|
12 |
8.1.2 |
Статистика и теория вероятности |
Умение находить статистические характеристики числового ряда |
Повышенный |
Со свободным, кратким однозначным ответом |
1 |
1 балл |
|
13 |
2.4.3 |
Тождественные преобразования |
Выполнение преобразований дробно-рациональных выражений, с использованием формул сокращенного умножения |
Повышенный |
С развернутым ответом |
5 |
2 балла
|
|
14 |
3.1.7 |
Уравнения и неравенства |
Умение находить точку пересечения графиков функций с помощью уравнения |
Повышенный |
С развернутым ответом |
5 |
2 балла |
|
15 |
3.3.2 |
Текстовые задачи |
Составление уравнение по заданным условиям, решение уравнений |
Повышенный |
С развернутым ответом |
10 |
2 балла
|
|
|
|
|
|
|
|
45 мин |
18 баллов |
Вариант I
1 часть
В каждом задании первой части необходимо записать верный ответ, в отведенном для этого месте. Каждый верный ответ оценивается в один балл.
16.
Вычислите:
![]()
Ответ:_____________________________
17. Найдите значение дроби: ![]() ,
,
Ответ:_____________________________
18. Сократите дробь ![]() , найдите значение дроби, если
, найдите значение дроби, если ![]() .
.
Ответ:_____________________________
19. Решите уравнение: ![]() , в ответе укажите наибольший из корней.
, в ответе укажите наибольший из корней.
Ответ:_____________________________
20. График функции ![]() проходит через точку К с ординатой 9.
Найдите абсциссу точки К.
проходит через точку К с ординатой 9.
Найдите абсциссу точки К.
Ответ:_____________________________
21. Найдите произведение корней
уравнения: ![]() .
.
Ответ:_____________________________
22. Пара чисел ![]() является решением системы
является решением системы ![]() . Найдите
. Найдите ![]() .
.
Ответ:_____________________________
23. Укажите наибольшее целое число,
удовлетворяющее условию ![]() , если
, если ![]() .
.
Ответ:_____________________________
24. В таблице представлены данные о количестве населения крупнейших (более 100 тыс. жителей), городов Челябинской области (на 4 декабря 2017г).
|
Город |
Количество жителей |
|
Челябинск |
1202371 |
|
Магнитогорск |
418241 |
|
Златоуст |
167978 |
|
Миасс |
151856 |
|
Копейск |
147573 |
Определите, во сколько раз численность населения Челябинска превышает численность населения Магнитогорска? (Ответ округлите до сотых).
Ответ: ________________________________
25. Определите, какие значения НЕ может
принимать переменная ![]() в выражении:
в выражении: ![]() ?
?
5) ![]()
6) ![]()
7) ![]()
8) ![]()
Ответ: _____________________________________
26. Упростите выражение: ![]()
5) ![]() ;
;
6) ![]() ;
;
7) ![]() ;
;
8) ![]() ;
;
Ответ: _______________________________________
27. На тренировке хоккейной команды «Трактор» девять игроков забили в ворота 19, 12, 17, 18, 14, 20, 23, 17, 21 шайбы соответственно. Найдите медиану полученного ряда чисел.
Ответ: ___________________________________
2 часть
Для записи решений и ответов каждого задания второй части используйте тетрадные листы в клетку. Запишите номер выполняемого задания, затем полное обоснованное решение и ответ. Каждое задание второй части оценивается от нуля до двух баллов.
28. Упростите выражение: ![]()
29. Найдите точки пересечения графиков
функций ![]()
30. Из Златоуста в санаторий «Увильды», расстояние между которыми равно120 км выехал автобус. Через 1 час вслед за ним выехал автомобиль, скорость которого больше скорости автобуса на 20км/ч. Автомобиль прибыл в конечный пункт одновременно с автобусом. Найдите скорость автобуса и автомобиля.
Вариант II
1 часть
В каждом задании первой части необходимо записать верный ответ, в отведенном для этого месте. Каждый верный ответ оценивается в один балл.
16.
Вычислите:
![]()
Ответ: _______________________
17.
Найдите
значение дроби:
![]() ,
,
Ответ: _______________________
18.
Сократите
дробь ![]() , найдите значение дроби, если
, найдите значение дроби, если ![]() .
.
Ответ: _______________________
19.
Решите
уравнение: ![]() , в ответе укажите наибольший из
корней.
, в ответе укажите наибольший из
корней.
Ответ: _______________________
20.
График
функции ![]() проходит через точку M с ординатой 4.
Найдите абсциссу точки M.
проходит через точку M с ординатой 4.
Найдите абсциссу точки M.
Ответ: _______________________
21.
Найдите
сумму корней уравнения: ![]() .
.
Ответ: ________________________
22.
Пара
чисел ![]() является решением системы
является решением системы ![]() . Найдите
. Найдите ![]() .
.
Ответ: ________________________
23.
Укажите
наименьшее целое число, удовлетворяющее условию ![]() , если
, если ![]() .
.
Ответ: ___________________________
24. В таблице представлены данные о количестве населения крупнейших (более 100 тыс. жителей), городов Челябинской области (на 4 декабря 2017г).
|
Город |
Количество жителей |
|
Челябинск |
1202371 |
|
Магнитогорск |
418241 |
|
Златоуст |
167978 |
|
Миасс |
151856 |
|
Копейск |
147573 |
Определите, во сколько раз численность населения Златоуста меньше численности населения Челябинска? (Ответ округлите до сотых). Ответ: ____________________________
25.
Определите,
какие значения НЕ может принимать переменная ![]() в выражении:
в выражении: ![]() ?
?
5)
![]()
6)
![]()
7)
![]()
8)
![]()
Ответ: ______________________________
26.
Упростите
выражение: ![]()
5)
![]() ;
;
6)
![]() ;
;
7)
![]() ;
;
8)
![]() ;
;
Ответ: _______________________________
27. На тренировке хоккейной команды «Трактор» деdять игроков забили в ворота 17, 22, 13, 15, 15, 19, 23, 20, 21 шайбы соответственно. Найдите медиану полученного ряда чисел.
Ответ: ____________________________
2 часть
Для записи решений и ответов каждого задания второй части используйте тетрадные листы в клетку. Запишите номер выполняемого задания, затем полное обоснованное решение и ответ. Каждое задание второй части оценивается от нуля до двух баллов.
28.
Упростите
выражение: ![]()
29.
Найдите
точки пересечения графиков функций ![]()
30. Из Полетаево в Челябинск, расстояние между которыми равно 30 км выехал велосипедист. Через 1 час вслед за ним выехал мотоциклист, скорость которого больше скорости велосипедиста на 40км/ч. Мотоциклист прибыл в конечный пункт одновременно с велосипедистом. Найдите скорость велосипедиста и мотоциклиста.
Планируемые результаты: Проверить уровень достижения результатов по основным темам курса математики 8 класса для обеспечения возможности успешного продолжения образования на базовом уровне.
Распределение заданий по разделам программ(ы)
|
№ п/п |
Раздел программы (содержательная линия) |
Количество заданий базового уровня сложности |
Количество заданий повышенного уровня сложности |
|
1. |
Числа и дроби |
3 |
|
|
2. |
Элементы теории множеств |
1 |
|
|
3. |
Тождественные преобразования |
2 |
1 |
|
4. |
Статистика, вероятность, комбинаторика |
1 |
|
|
5. |
Уравнения и неравенства |
3 |
|
|
6 |
Функции |
2 |
1 |
|
7 |
Текстовые задачи |
|
1 |
|
|
Всего |
12 |
3 |
Инструкция по проверке и оценке работ
|
№ задания |
Планируемый результат |
Правильный ответ |
Критерии оценивания / Максимальный балл |
||
|
Вариант 1 |
Вариант 2 |
||||
|
1 |
Вычисление арифметического квадратного корня |
10,9 |
|
1 балл |
|
|
2 |
Применение свойств степени с целым показателем |
3 |
2 |
1 балл |
|
|
3 |
Преобразование рациональных дробей |
1,5 |
2,25 |
1 балл |
|
|
4 |
Решение квадратных уравнений |
3 |
4 |
1 балл |
|
|
5 |
Определение принадлежности точки, графику функции |
81 |
16 |
1 балл |
|
|
6 |
Применение теоремы Виета |
|
1 |
1 балл |
|
|
7 |
Решение системы линейных уравнений |
|
9 |
1 балл |
|
|
8 |
Выполнение действий с множествами, пересечение множеств |
|
|
1 балл |
|
|
9 |
Работа с таблицами |
2,87 |
7,16 |
1 балл |
|
|
10 |
Нахождение области допустимых значений переменной |
3 |
3 |
1 балл |
|
|
11 |
Применение свойств арифметического квадратного корня |
3 |
4 |
1 балл |
|
|
12 |
Определение статистических характеристик ряда чисел |
18 |
19 |
1 балл |
|
|
13 |
Преобразование дробно-рациональных выражений |
|
|
2 балла правильно выполнены преобразования, получен верный ответ. 1 балл решение доведено до конца, но допущена ошибка вычислительного характера или описка, с ее учетом дальнейшие шаги выполнены верно. 0 баллов другие случаи, не соответствующие указанным критериям |
|
|
14 |
Пересечение графиков функций, решение уравнения или системы уравнений. |
|
|
2 балла верно и обоснованно найдены точки пересечения графиков. 1 балл при верных рассуждениях допущена вычислительная ошибка, или описка, возможно приведшая к неверному ответу. 0 баллов другие случаи, не соответствующие указанным критериям |
|
|
15 |
Решение текстовых задач с помощью уравнения |
40км/ч; 60км/ч. |
20км/ч; 60км/ч. |
2 балла получен верный обоснованный ответ. 1 балл при верных рассуждениях допущена вычислительная ошибка, возможно приведшая к неверному ответу. 0 баллов другие случаи, не соответствующие указанным критериям |
|
Контрольная работа № 1 «Квадратный трехчлен»
План контрольной работы
|
№ задания |
КЭС (код) |
Раздел программы (содержательная линия) |
Проверяемый планируемый результат |
Уровень сложности |
Тип задания |
Время выполнения |
Максимальный балл |
|
1 |
3.1.1 |
Уравнения и неравенства |
Нахождение корней квадратного трёхчлена |
Базовый |
С кратким ответом |
4 |
1 балл |
|
2 |
3.1.3 |
Уравнения и неравенства |
Определение числа корней квадратного трёхчлена |
Базовый |
С кратким ответом |
4 |
1 балл |
|
3 |
3.1.5 |
Тождественные преобразования |
Разложение квадратного трёхчлена на множители, вынесение общего множителя за скобки |
Базовый |
С кратким ответом |
4 |
1 балл |
|
4 |
3.1.5 |
Тождественные преобразования |
Выделение полного квадрата из квадратного трёхчлена |
Базовый |
С выбором ответа |
4 |
1 балл |
|
5 |
3.1.5 |
Уравнения и неравенства |
Разложение квадратного трёхчлена на множители |
Базовый |
С кратким ответом |
4 |
1 балл |
|
6 |
3.1.5 |
Тождественные преобразования |
Тождественные преобразования алгебраических дробей с использованием разложения квадратного трёхчлена на множители |
Повышенный |
С развернутым ответом |
10 |
2 балла |
|
7 |
3.2.5 |
Уравнения и неравенства |
Решение квадратных неравенств с параметром |
Повышенный |
С развернутым ответом |
10 |
2 балла |
|
|
|
|
|
|
|
40 мин |
Общий балл |
Вариант I
1 часть
В каждом задании первой части необходимо записать верный ответ, в отведенном для этого месте. Каждый верный ответ оценивается в один балл.
8.
Найдите
больший корень квадратного трёхчлена ![]() .
.
Ответ:_________
9.
Сколько
корней имеет квадратный трёхчлен ![]() .
.
Ответ:_________
10.
Найдите
значение дроби ![]() при
при ![]() .
.
Ответ:_________
11. Выделите
квадрат двучлена из квадратного трёхчлена ![]() .
.
9) ![]()
10)
![]()
11) ![]()
12) ![]()
Ответ:_________
12. Разложите
на множители квадратный трёхчлен ![]() .
.
Ответ:__________
II часть
Для записи решений и ответов каждого задания второй части используйте тетрадные листы в клетку. Запишите номер выполняемого задания, затем полное обоснованное решение и ответ. Каждое задание второй части оценивается от нуля до двух баллов.
13.
Упростите
выражение: ![]() .
.
14.
При
каких значениях ![]() квадратный трёхчлен
квадратный трёхчлен ![]() принимает только
отрицательные значения?
принимает только
отрицательные значения?
Вариант II
1 часть
В каждом задании первой части необходимо записать верный ответ, в отведенном для этого месте. Каждый верный ответ оценивается в один балл.
1.
Найдите меньший корень квадратного трёхчлена ![]() .
.
Ответ:_________
2.
Сколько корней имеет квадратный трёхчлен ![]() .
.
Ответ:_________
3.
Найдите значение дроби ![]() при
при ![]() .
.
Ответ:_________
4.
Выделите квадрат двучлена из квадратного трёхчлена ![]() .
.
17) ![]()
18)
![]()
19) ![]()
20) ![]()
Ответ:__________
5.
Разложите на множители квадратный трёхчлен ![]() .
.
Ответ:__________
II часть
Для записи решений и ответов каждого задания второй части используйте тетрадные листы в клетку. Запишите номер выполняемого задания, затем полное обоснованное решение и ответ. Каждое задание второй части оценивается от нуля до двух баллов.
6.
Упростите выражение: ![]() .
.
7.
При каких значениях ![]() квадратный трёхчлен
квадратный трёхчлен ![]() принимает только отрицательные
значения?
принимает только отрицательные
значения?
Инструкция по проверке и оценке работ
|
№ задания |
Планируемый результат |
Правильный ответ |
Критерии оценивания / Максимальный балл |
|
|
1 вариант |
2 вариант |
|||
|
1 |
Нахождение корней квадратного трёхчлена. Сравнение чисел |
-0,5 |
|
За верный ответ 1 балл |
|
2 |
Определение числа корней квадратного трёхчлена по знаку дискриминанта |
2 |
2 |
За верный ответ 1 балл |
|
3 |
Разложение квадратного трёхчлена на множители, вынесение общего множителя за скобки, вычисление значения выражения при заданном значении переменной |
-0,8 |
0,8 |
За верный ответ 1 балл |
|
4 |
Выделение полного квадрата из квадратного трёхчлена |
3 |
4 |
За верный ответ 1 балл |
|
5 |
Разложение квадратного трёхчлена на множители |
|
|
За верный ответ 1 балл |
|
6 |
Тождественные преобразования алгебраических дробей с использованием разложения квадратного трёхчлена на множители |
|
|
2 балла получен верный обоснованный ответ. 1 балл при верных рассуждениях допущена вычислительная ошибка или описка, возможно приведшая к неверному ответу. 0 баллов другие случаи, не соответствующие указанным критериям |
|
7 |
Решение квадратных неравенств с параметром. Выполнение оценки правдоподобия полученных результатов
|
|
|
2 балла получен верный обоснованный ответ. 1 балл при верных рассуждениях допущена вычислительная ошибка или описка, возможно приведшая к неверному ответу. 0 баллов другие случаи, не соответствующие указанным критериям |
|
|
|
|
Итого 9 |
|
Контрольная работа № 2 «Квадратичная и степенная функции»
План контрольной работы
|
№ задания |
КЭС (код) |
Раздел программы (содержательная линия) |
Проверяемый планируемый результат |
Уровень сложности |
Тип задания |
Время выполнения |
Максимальный балл |
|
1 |
5.1.1 |
Числа. Функции |
Сравнение чисел с использованием свойств степенной функции |
Базовый |
С кратким ответом |
4 |
1 балл |
|
2 |
5.1.1 |
Функции |
Вычисление значений степенной функции |
Базовый |
С кратким ответом |
4 |
1 балл |
|
3 |
1.4.3 |
Числа |
Вычисление корня n-ой степени |
Базовый |
С кратким ответом |
4 |
1 балл |
|
4 |
1.4.5 |
Числа. Функции |
Сравнение чисел с использованием свойств функции |
Базовый |
С выбором ответа |
4 |
1 балл |
|
5 |
1.4.5 |
Числа |
Нахождение области допустимых значений переменной |
Базовый |
С кратким ответом |
4 |
1 балл |
|
6 |
3.1.5 |
Уравнения и неравенства |
Решение уравнения методом замены переменной. Выполнение оценки правдоподобия полученных результатов |
Повышенный |
С развернутым ответом |
10 |
2 балла |
|
7 |
2.3.2 |
Числа. Тождественные преобразования |
Нахождение значения выражения содержащего корни n-ой степени с использованием формул сокращённого умножения |
Повышенный |
С развернутым ответом |
10 |
2 балла |
|
|
|
|
|
|
|
40 мин |
Общий балл |
Вариант I
1 часть
В каждом задании первой части необходимо записать верный ответ, в отведенном для этого месте. Каждый верный ответ оценивается в один балл.
1. Что
больше ![]() ?
?
Ответ:_________
2. Вычислите
![]() , если
, если ![]() .
.
Ответ:_________
3. Найдите
значение выражения ![]() .
.
Ответ:_________
4. Расположите
числа ![]() в порядке возрастания.
в порядке возрастания.
13) ![]()
14) ![]()
15) ![]()
16) ![]()
Ответ:_________
5. При
каких значениях![]() верно равенство
верно равенство ![]() .
.
Ответ:__________
II часть
Для записи решений и ответов каждого задания второй части используйте тетрадные листы в клетку. Запишите номер выполняемого задания, затем полное обоснованное решение и ответ. Каждое задание второй части оценивается от нуля до двух баллов.
6. Решите
уравнение: ![]() .
.
7. Вычислите
значение выражения: ![]()
Вариант II
1 часть
В каждом задании первой части необходимо записать верный ответ, в отведенном для этого месте. Каждый верный ответ оценивается в один балл.
1.
Что меньше ![]() ?
?
Ответ:_________
2.
Вычислите ![]() , если
, если ![]() .
.
Ответ:_________
3.
Найдите значение выражения ![]() .
.
Ответ:_________
4.
Расположите числа ![]() в порядке возрастания.
в порядке возрастания.
21) ![]()
22) ![]()
23) ![]()
24) ![]()
Ответ:__________
5.
При каких значениях![]() верно равенство
верно равенство ![]()
Ответ:__________
II часть
Для записи решений и ответов каждого задания второй части используйте тетрадные листы в клетку. Запишите номер выполняемого задания, затем полное обоснованное решение и ответ. Каждое задание второй части оценивается от нуля до двух баллов.
6.
Решите уравнение: ![]() .
.
7.
Вычислите значение выражения: ![]() .
.
Инструкция по проверке и оценке работ
|
№ задания |
Планируемый результат |
Правильный ответ |
Критерии оценивания / Максимальный балл |
|
|
1 вариант |
2 вариант |
|||
|
1 |
Сравнение чисел с использованием свойств степенной функции |
А |
А |
За верный ответ 1 балл |
|
2 |
Вычисление значений степенной функции |
19 |
-65 |
За верный ответ 1 балл |
|
3 |
Вычисление корня n-ой степени |
2 |
-2 |
За верный ответ 1 балл |
|
4 |
Сравнение чисел с использованием свойств функции. НОК |
4 |
1 |
За верный ответ 1 балл |
|
5 |
Нахождение области допустимых значений переменной. Применение свойств корня n-ой степени |
|
|
За верный ответ 1 балл |
|
6 |
Решение уравнения методом замены переменной. Выполнение оценки правдоподобия полученных результатов |
|
|
2 балла получен верный обоснованный ответ. 1 балл при верных рассуждениях допущена вычислительная ошибка или описка, возможно приведшая к неверному ответу. 0 баллов другие случаи, не соответствующие указанным критериям |
|
7 |
Нахождение значения выражения с использованием формул сокращённого умножения и свойств корня n-ой степени |
3 |
3 |
2 балла получен верный обоснованный ответ. 1 балл при верных рассуждениях допущена вычислительная ошибка или описка, возможно приведшая к неверному ответу. 0 баллов другие случаи, не соответствующие указанным критериям |
|
|
|
|
Итого 9 |
|
Контрольная работа № 3 «Решение уравнений и неравенств с одной переменной»
План контрольной работы
|
№ задания |
КЭС (код) |
Раздел программы (содержательная линия) |
Проверяемый планируемый результат |
Уровень сложности |
Тип задания |
Время выполнения |
Максимальный балл |
|
1 |
3.2.5 |
Уравнения и неравенства |
Решение квадратных неравенств |
Базовый |
С кратким ответом |
4 |
1 балл |
|
2 |
3.2.5 |
Уравнения и неравенства |
Решение квадратных неравенств |
Базовый |
С кратким ответом |
4 |
1 балл |
|
3 |
3.2.5 |
Уравнения и неравенства |
Решение квадратных неравенств |
Базовый |
С кратким ответом |
4 |
1 балл |
|
4 |
3.2.5 |
Уравнения и неравенства |
Решение квадратных неравенств |
Базовый |
С выбором ответа |
4 |
1 балл |
|
5 |
3.2.5 |
Уравнения и неравенства |
Решение квадратных неравенств |
Базовый |
С кратким ответом |
4 |
1 балл |
|
6 |
3.2.5 |
Уравнения и неравенства |
Решение квадратных неравенств. Сравнение буквенных выражений |
Повышенный |
С развернутым ответом |
10 |
2 балла |
|
7 |
5.1.1 |
Функции |
Нахождение области определения функции |
Повышенный |
С развернутым ответом |
10 |
2 балла |
|
|
|
|
|
|
|
40 мин |
Общий балл |
Вариант I
1 часть
В каждом задании первой части необходимо записать верный ответ, в отведенном для этого месте. Каждый верный ответ оценивается в один балл.
1.
Запишите
наименьшее натуральное число удовлетворяющее неравенству ![]() .
.
Ответ:_________
2.
Решить
неравенство ![]() .
.
Ответ:_________
3.
Укажите
наибольшее целое ![]() удовлетворяющее
неравенству
удовлетворяющее
неравенству ![]() .
.
Ответ:_________
4.
Решением
неравенства ![]() является:
является:
![]()
2.неравенство не имеет решений
![]()
4.(![]()
Ответ:_________
5.
Решите
неравенство ![]() .
.
Ответ:__________
II часть
Для записи решений и ответов каждого задания второй части используйте тетрадные листы в клетку. Запишите номер выполняемого задания, затем полное обоснованное решение и ответ. Каждое задание второй части оценивается от нуля до двух баллов.
6.
Что
больше: ![]() или
или ![]() ?
?
7.
Найдите
область определения функции ![]()
Вариант II
1 часть
В каждом задании первой части необходимо записать верный ответ, в отведенном для этого месте. Каждый верный ответ оценивается в один балл.
1. Запишите наименьшее натуральное число
удовлетворяющее неравенству ![]() ..
..
Ответ:_________
2.
Решить неравенство ![]() .
.
Ответ:_________
3. Укажите наибольшее целое ![]() удовлетворяющее
неравенству
удовлетворяющее
неравенству ![]() .
.
Ответ:_________
4.
Решением неравенства ![]() является:
является:
![]()
2.неравенство не имеет решений
3.![]()
4.(![]()
Ответ:__________
5.
Решите неравенство ![]() .
.
Ответ:__________
II часть
Для записи решений и ответов каждого задания второй части используйте тетрадные листы в клетку. Запишите номер выполняемого задания, затем полное обоснованное решение и ответ. Каждое задание второй части оценивается от нуля до двух баллов.
6.
Что больше: ![]() или
или ![]() ?
?
7.
Найдите область определения функции ![]()
Инструкция по проверке и оценке работ
|
№ задания |
Планируемый результат |
Правильный ответ |
Критерии оценивания / Максимальный балл |
|
|
1 вариант |
2 вариант |
|||
|
1 |
Решение квадратных неравенств. Корректная запись решения неравенства |
1 |
1 |
За верный ответ 1 балл |
|
2 |
Решение квадратных неравенств. Корректная запись решения неравенства (в том числе используя математическую символику) |
|
|
За верный ответ 1 балл |
|
3 |
Решение квадратных неравенств. Корректная запись решения неравенства |
3 |
2 |
За верный ответ 1 балл |
|
4 |
Решение квадратных неравенств. |
4 |
2 |
За верный ответ 1 балл |
|
5 |
Решение квадратных неравенств |
2,5 |
1,5 |
За верный ответ 1 балл |
|
6 |
Решение квадратных неравенств. Сравнение буквенных выражений. |
В |
В |
2 балла получен верный обоснованный ответ. 1 балл при верных рассуждениях допущена вычислительная ошибка или описка, возможно приведшая к неверному ответу. 0 баллов другие случаи, не соответствующие указанным критериям |
|
7 |
Нахождение области определения функции. Решение квадратных неравенств. Корректная запись решения неравенства (в том числе используя математическую символику) |
|
|
2 балла получен верный обоснованный ответ. 1 балл при верных рассуждениях допущена вычислительная ошибка или описка, возможно приведшая к неверному ответу. 0 баллов другие случаи, не соответствующие указанным критериям |
|
|
|
|
Итого 9 |
|
Контрольная работа № 4 «Решение систем уравнений и неравенств с двумя переменными»
План контрольной работы
|
№ задания |
КЭС (код) |
Раздел программы (содержательная линия) |
Проверяемый планируемый результат |
Уровень сложности |
Тип задания |
Время выполнения |
Максимальный балл |
|
1 |
3.2.4 |
Уравнения и неравенства |
Решение систем линейных уравнений |
Базовый |
С кратким ответом |
4 |
1 балл |
|
2 |
3.2.4 |
Уравнения и неравенства. Функции |
Графическое решение систем уравнений |
Базовый |
С кратким ответом |
4 |
1 балл |
|
3 |
3.2.4 |
Уравнения и неравенства |
Решение систем уравнений методом замены |
Базовый |
С кратким ответом |
4 |
1 балл |
|
4 |
3.2.4 |
Уравнения и неравенства |
Решение систем уравнений. Выполнение оценки правдоподобия предложенных решений систем уравнений |
Базовый |
С выбором ответа |
4 |
1 балл |
|
5 |
5.1.8 |
Функция |
Графическое решение систем уравнений |
Базовый |
С кратким ответом |
4 |
1 балл |
|
6 |
3.3.2 |
Текстовые задачи |
Решение текстовых задач на составление системы уравнений |
Повышенный |
С развернутым ответом |
10 |
2 балла |
|
7 |
3.2.4 |
Уравнения и неравенства |
Решение систем уравнений с использованием определения модуля. Выполнение оценки правдоподобия полученных результатов |
Повышенный |
С развернутым ответом |
10 |
2 балла |
|
|
|
|
|
|
|
40 мин |
Общий балл |
Вариант I
1 часть
В каждом задании первой части необходимо записать верный ответ, в отведенном для этого месте. Каждый верный ответ оценивается в один балл.
1. Найдите
решение системы уравнений ![]() .
.
Ответ:_________
2. Сколько
решений имеет система уравнений ![]()
Ответ:_________
3. Пара
![]() является решением
системы
является решением
системы 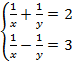 . В ответ запишите
. В ответ запишите ![]() .
.
Ответ:_________
4.
Решением
системы уравнений ![]() является пара чисел:
является пара чисел:
17) ![]()
18) ![]()
19) ![]()
20) ![]()
Ответ:_________
5. Найдите
координаты точек пересечения параболы ![]() и прямой
и прямой ![]() .
.
Ответ:__________
II часть
Для записи решений и ответов каждого задания второй части используйте тетрадные листы в клетку. Запишите номер выполняемого задания, затем полное обоснованное решение и ответ. Каждое задание второй части оценивается от нуля до двух баллов.
6. По течению реки моторная лодка проходит 40 км за 2 часа, а против течения проходит 35 км за 2 часа и 30 минут. Найдите скорость течения реки.
7. Решите
систему уравнений: ![]() .
.
Вариант II
1 часть
В каждом задании первой части необходимо записать верный ответ, в отведенном для этого месте. Каждый верный ответ оценивается в один балл.
1.
Найдите решение системы уравнений ![]() .
.
Ответ:_________
2.
Сколько решений имеет система уравнений ![]()
Ответ:_________
3. Пара ![]() является решением
системы
является решением
системы  . В ответ запишите
. В ответ запишите ![]() .
.
Ответ:_________
4.
Решением системы уравнений ![]() является пара чисел:
является пара чисел:
25) ![]()
26) ![]()
27) ![]()
28) ![]()
Ответ:__________
5.
Найдите координаты точек пересечения параболы ![]() и прямой
и прямой ![]() .
.
Ответ:__________
II часть
Для записи решений и ответов каждого задания второй части используйте тетрадные листы в клетку. Запишите номер выполняемого задания, затем полное обоснованное решение и ответ. Каждое задание второй части оценивается от нуля до двух баллов.
6. По течению реки моторная лодка проходит 40 км за 2 часа, а против течения проходит 35 км за 2 часа и 30 минут. Найдите скорость течения реки.
7. Решите систему уравнений: ![]() .
.
Инструкция по проверке и оценке работ
|
№ задания |
Планируемый результат |
Правильный ответ |
Критерии оценивания / Максимальный балл |
|
|
1 вариант |
2 вариант |
|||
|
1 |
Решение систем линейных уравнений |
|
|
За верный ответ 1 балл |
|
2 |
Графическое решение систем уравнений. Выполнение оценки возможных результатов |
3 |
3 |
За верный ответ 1 балл |
|
3 |
Решение систем уравнений методом замены |
-1,6 |
-1,6 |
За верный ответ 1 балл |
|
4 |
Решение систем уравнений. Выполнение оценки правдоподобия предложенных решений систем уравнений |
3 |
4 |
За верный ответ 1 балл |
|
5 |
Графическое решение систем уравнений. Решение квадратного уравнения |
|
|
За верный ответ 1 балл |
|
6 |
Решение текстовых задач на составление системы уравнений |
3 |
3 |
2 балла получен верный обоснованный ответ. 1 балл при верных рассуждениях допущена вычислительная ошибка или описка, возможно приведшая к неверному ответу. 0 баллов другие случаи, не соответствующие указанным критериям |
|
7 |
Решение систем уравнений с использованием определения модуля. Выполнение оценки правдоподобия полученных результатов |
|
|
2 балла получен верный обоснованный ответ. 1 балл при верных рассуждениях допущена вычислительная ошибка или описка, возможно приведшая к неверному ответу. 0 баллов другие случаи, не соответствующие указанным критериям |
|
|
|
|
Итого 9 |
|
Контрольная работа № 5 «Арифметическая прогрессия»
План контрольной работы
|
№ задания |
КЭС (код) |
Раздел программы (содержательная линия) |
Проверяемый планируемый результат |
Уровень сложности |
Тип задания |
Время выполнения |
Максимальный балл |
|
1 |
4.2.1 |
функция |
Находить неизвестный член последовательности |
Базовый |
С кратким ответом |
4 мин |
1 балл |
|
2 |
4.2.1 |
функция |
Применять формулу n-ого члена прогрессии |
Базовый |
С кратким ответом |
4 мин |
1 балл |
|
3 |
4.2.1 |
функция |
Применять формулу n-ого члена прогрессии |
Базовый |
С кратким ответом |
4 мин |
1 балл |
|
4 |
4.2.1 |
функция |
Использование характеристическое свойство прогрессии |
Базовый |
С выбором ответа |
4 мин |
1 балл |
|
5 |
4.2.1 |
функция |
Нахождение первых членов прогрессии |
Базовый |
С кратким ответом |
4 мин |
1 балл |
|
6 |
4.2.1 |
функция |
Нахождение неизвестных членов последовательности, анализ полученных данных |
Повышенный |
С развернутым ответом |
10 мин |
2 балла |
|
7 |
4.2.2 |
функция |
Нахождение неизвестных членов последовательности, анализ полученных данных |
Повышенный |
С развернутым ответом |
10 мин |
2 балла |
|
|
|
|
|
|
|
40 мин |
Общий балл |
Вариант I
1 часть
В каждом задании первой части необходимо записать верный ответ, в отведенном для этого месте. Каждый верный ответ оценивается в один балл.
1. Выписано
несколько последовательных членов арифметической прогрессии: ![]() Найдите член прогрессии,
обозначенный буквой
Найдите член прогрессии,
обозначенный буквой ![]() .
.
Ответ:_________
2. Арифметическая
прогрессия задана формулой n-го
члена ![]() . Найдите разность
прогрессии.
. Найдите разность
прогрессии.
Ответ:_________
3. Найдите
девятый член арифметической прогрессии, если ![]() .
.
Ответ:_________
4. Последовательности заданы несколькими первыми членами. Одна из них – арифметическая прогрессия. Укажите её.
1. ![]()
2. ![]()
3. ![]()
4. ![]()
Ответ:_________
5. Сколько последовательных натуральных чисел, начиная с 1, нужно сложить, чтобы их сумма была равна 120?
Ответ:__________
II часть
Для записи решений и ответов каждого задания второй части используйте тетрадные листы в клетку. Запишите номер выполняемого задания, затем полное обоснованное решение и ответ. Каждое задание второй части оценивается от нуля до двух баллов.
6. Первый член арифметической прогрессии равен 6, а её разность равна 4. Начиная с какого номера члены этой прогрессии больше 258?
7. Найдите сумму всех натуральных чисел, не превосходящих 200, которые НЕ делятся на 6.
Вариант II
1 часть
В каждом задании первой части необходимо записать верный ответ, в отведенном для этого месте. Каждый верный ответ оценивается в один балл.
1.
Выписано несколько последовательных членов арифметической прогрессии: ![]() Найдите член прогрессии,
обозначенный буквой
Найдите член прогрессии,
обозначенный буквой ![]() .
.
Ответ:_________
2.
Арифметическая прогрессия задана формулой n-го
члена ![]() . Найдите разность
прогрессии.
. Найдите разность
прогрессии.
Ответ:_________
3.
Найдите седьмой член арифметической прогрессии, если ![]() .
.
Ответ:_________
4. Последовательности заданы несколькими первыми членами. Одна из них – арифметическая прогрессия. Укажите её.
1.![]()
2.
![]()
![]()
![]()
Ответ:__________
5. Сколько последовательных натуральных чисел, начиная с 1, нужно сложить, чтобы их сумма была равна 105?
Ответ:__________
II часть
Для записи решений и ответов каждого задания второй части используйте тетрадные листы в клетку. Запишите номер выполняемого задания, затем полное обоснованное решение и ответ. Каждое задание второй части оценивается от нуля до двух баллов.
6. Первый член арифметической прогрессии равен 6, а её разность равна 4. Начиная с какого номера члены этой прогрессии больше 258?
7. Найдите сумму всех натуральных чисел, не превосходящих 200, которые НЕ делятся на 6.
Инструкция по проверке и оценке работ
|
№ задания |
Планируемый результат |
Правильный ответ |
Критерии оценивания / Максимальный балл |
|
|
1 вариант |
2 вариант |
|||
|
1 |
Нахождение неизвестного члена последовательности по определению |
|
|
За верный ответ 1 балл |
|
2 |
Нахождение неизвестного члена последовательности по формуле |
4 |
3 |
За верный ответ 1 балл |
|
3 |
Нахождение неизвестного члена последовательности по формуле |
16,9 |
14,3 |
За верный ответ 1 балл |
|
4 |
Применение характеристического свойства прогрессии |
3 |
2 |
За верный ответ 1 балл |
|
5 |
Нахождение первых членов прогрессии по формулам |
15 |
14 |
За верный ответ 1 балл |
|
6 |
Нахождение первых членов прогрессии по формулам, анализ полученных результатов |
|
|
2 балла получен верный обоснованный ответ. 1 балл при верных рассуждениях допущена вычислительная ошибка или описка, возможно приведшая к неверному ответу. 0 баллов другие случаи, не соответствующие указанным критериям |
|
7 |
Нахождение первых членов прогрессии по формулам, анализ полученных результатов |
16734 |
16734 |
2 балла получен верный обоснованный ответ. 1 балл при верных рассуждениях допущена вычислительная ошибка или описка, возможно приведшая к неверному ответу. 0 баллов другие случаи, не соответствующие указанным критериям |
|
|
|
|
Итого 9 |
|
Контрольная работа № 6 «Геометрическая прогрессия»
План контрольной работы
|
№ задания |
КЭС (код) |
Раздел программы (содержательная линия) |
Проверяемый планируемый результат |
Уровень сложности |
Тип задания |
Время выполнения |
Максимальный балл |
|
1 |
4.2.3 |
функция |
Находить неизвестный член последовательности |
Базовый |
С кратким ответом |
4 мин |
1 балл |
|
2 |
4.2.3 |
функция |
Применять формулу n-ого члена прогрессии |
Базовый |
С кратким ответом |
4 мин |
1 балл |
|
3 |
4.2.3 |
функция |
Применять формулу n-ого члена прогрессии |
Базовый |
С кратким ответом |
4 мин |
1 балл |
|
4 |
4.2.3 |
функция |
Задать формулу n-ого члена прогрессии |
Базовый |
С выбором ответа |
4 мин |
1 балл |
|
5 |
4.2.4 |
функция |
Нахождение первых членов прогрессии |
Базовый |
С кратким ответом |
4 мин |
1 балл |
|
6 |
4.2.4 |
функция |
Нахождение неизвестных членов последовательности, анализ полученных данных |
Повышенный |
С развернутым ответом |
10 мин |
2 балла |
|
7 |
4.2.3 |
функция |
Нахождение неизвестных членов последовательности, анализ полученных данных |
Повышенный |
С развернутым ответом |
10 мин |
2 балла |
|
|
|
|
|
|
|
40 мин |
Общий балл |
Вариант I
1 часть
В каждом задании первой части необходимо записать верный ответ, в отведенном для этого месте. Каждый верный ответ оценивается в один балл.
1. Выписано
несколько последовательных членов геометрической прогрессии: ![]() Найдите член прогрессии,
обозначенный буквой
Найдите член прогрессии,
обозначенный буквой ![]() .
.
Ответ:_________
2. Найдите
шестой член геометрической прогрессии ![]()
Ответ:_________
3. Найдите
первый член геометрической прогрессии, если ![]() .
.
Ответ:_________
4.
Геометрическая
прогрессия задана условиями: ![]() . Укажите формулу общего
члена этой прогрессии.
. Укажите формулу общего
члена этой прогрессии.
21)
![]()
22)
![]()
23)
![]()
24)
![]()
Ответ:_________
5. Первый
член геометрической прогрессии ![]() , знаменатель
, знаменатель ![]() ,
а сумма
,
а сумма ![]() первых членов
первых членов ![]() . Найдите число
. Найдите число ![]() .
.
Ответ:__________
II часть
Для записи решений и ответов каждого задания второй части используйте тетрадные листы в клетку. Запишите номер выполняемого задания, затем полное обоснованное решение и ответ. Каждое задание второй части оценивается от нуля до двух баллов.
6.
Найдите
сумму первых шести членов геометрической прогрессии, если её четвёртый член
равен ![]() , а знаменатель равен
0,5.
, а знаменатель равен
0,5.
7.
При
каких значениях![]() числа
числа ![]() являются четырьмя
последовательными членами геометрической прогрессии?
являются четырьмя
последовательными членами геометрической прогрессии?
Вариант II
1 часть
В каждом задании первой части необходимо записать верный ответ, в отведенном для этого месте. Каждый верный ответ оценивается в один балл.
1.
Выписано несколько последовательных членов геометрической прогрессии: ![]() Найдите член прогрессии,
обозначенный буквой
Найдите член прогрессии,
обозначенный буквой ![]() .
.
Ответ:_________
2.
Найдите шестой член геометрической прогрессии ![]()
Ответ:_________
3.
Найдите первый член геометрической прогрессии, если ![]() .
.
Ответ:_________
4.
Геометрическая прогрессия задана условиями: ![]() . Укажите формулу общего
члена этой прогрессии.
. Укажите формулу общего
члена этой прогрессии.
29)
![]()
30)
![]()
31)
![]()
32)
![]()
Ответ:__________
5.
Первый член геометрической прогрессии ![]() , знаменатель
, знаменатель ![]() ,
а сумма
,
а сумма ![]() первых членов
первых членов ![]() . Найдите число
. Найдите число ![]() .
.
Ответ:__________
II часть
Для записи решений и ответов каждого задания второй части используйте тетрадные листы в клетку. Запишите номер выполняемого задания, затем полное обоснованное решение и ответ. Каждое задание второй части оценивается от нуля до двух баллов.
6. Найдите сумму первых шести членов
геометрической прогрессии, если её четвёртый член равен ![]() , а знаменатель равен
0,5.
, а знаменатель равен
0,5.
7. При каких значениях![]() числа
числа ![]() являются четырьмя
последовательными членами геометрической прогрессии?
являются четырьмя
последовательными членами геометрической прогрессии?
Инструкция по проверке и оценке работ
|
№ задания |
Планируемый результат |
Правильный ответ |
Критерии оценивания / Максимальный балл |
|
|
1 вариант |
2 вариант |
|||
|
1 |
Нахождение неизвестного члена последовательности по определению |
|
|
За верный ответ 1 балл |
|
2 |
Нахождение неизвестного члена последовательности по формуле |
0,75 |
4,5 |
За верный ответ 1 балл |
|
3 |
Нахождение неизвестного члена последовательности по формуле |
|
|
За верный ответ 1 балл |
|
4 |
Задание прогрессии формулой n-ого члена |
3 |
1 |
За верный ответ 1 балл |
|
5 |
Нахождение первых членов прогрессии по формулам |
8 |
8 |
За верный ответ 1 балл |
|
6 |
Нахождение первых членов прогрессии по формулам, анализ полученных результатов |
|
|
2 балла получен верный обоснованный ответ. 1 балл при верных рассуждениях допущена вычислительная ошибка или описка, возможно приведшая к неверному ответу. 0 баллов другие случаи, не соответствующие указанным критериям |
|
7 |
Нахождение первых членов прогрессии по формулам, анализ полученных результатов |
1 |
1 |
2 балла получен верный обоснованный ответ. 1 балл при верных рассуждениях допущена вычислительная ошибка или описка, возможно приведшая к неверному ответу. 0 баллов другие случаи, не соответствующие указанным критериям |
|
|
|
|
Итого 9 |
|
Контрольная работа № 7 «Элементы комбинаторики и теории вероятностей»
План контрольной работы
Перечень элементов содержания
|
Код контролируемого элемента |
Элементы содержания, проверяемые заданиями диктанта
|
|
8 |
Статистика и теория вероятности |
|
8.1.2 |
Среднее результатов измерений |
|
8.2.1 |
Частота события, вероятность |
|
8.2.2 |
Равновозможные события и подсчет их вероятности |
|
8.3.1 |
Решение комбинаторных задач |
ОТВЕТЫ И КРИТЕРИИ ОЦЕНИВАНИЯ
1) Десять детей младшей группы по плаванию Челябинского бассейна «Строитель» в соревнованиях показали следующие результаты (в секундах): 44, 32, 29, 31, 48, 28, 42, 33, 38, 35. Установите соответствие между статистическими характеристиками этого ряда и их численными значениями:
А. Среднее арифметическое. 1) 34
Б. Медиана ряда. 2) 20
В. Размах ряда. 3) 0
Г. Сумма всех отклонений от среднего арифметического. 4) 38
Ответ:
|
А |
Б |
В |
Г |
|
4 |
1 |
2 |
3 |
(4 балла)
2) Сколько можно записать различных трехзначных чисел без повторения, используя только цифры 0, 2, 7 и 9?
Ответ: 18 (1 балл)
3) На студенческую конференцию собрались 7 студентов из Екатеринбурга, 3 из Магнитогорска, 6 из Перми и 9 из Челябинска. Порядок докладов определяется жеребьевкой. Найдите вероятность того, что вторым окажется доклад студента из Перми.
Ответ: 0,12 (1 балл)
4)На отрезок ![]() бросают случайную точку. Какова
вероятность того, что ее координата будет меньше 1?
бросают случайную точку. Какова
вероятность того, что ее координата будет меньше 1?
Ответ: ![]() (1 балл)
(1 балл)
5) Два пассажира садятся в электричку из восьми вагонов следующую до станции Челябинск – Главный. С какой вероятностью они окажутся в разных вагонах, если каждый из них выбирает вагон случайным образом?
Ответ: ![]() (1
балл)
(1
балл)
6) В магазине стоят два платежных автомата. Каждый из них может быть неисправен с вероятностью 0,05. Найдите вероятность того, что хотя бы один автомат исправен?
Ответ: 0,9975 (1 балл)
За правильный ответ в задании 1 ставиться 1 балл за каждый пункт; за верный ответ в заданиях 2-6 ставится 1 балл.
Итоговая контрольная работа
План диагностической работы
|
№ задания |
КЭС (код) |
Раздел программы (содержательная линия) |
Проверяемый планируемый результат |
Уровень сложности |
Тип задания |
Время выполнения (мин) |
Максимальный балл |
|
1 |
1.2.5 |
Числа и дроби |
использовать свойства чисел и правила действий при выполнении вычислений |
Базовый |
С установлением соответствия |
3 |
1 балл |
|
2 |
6.1.1 |
Числа и дроби |
использовать свойства чисел и правила действий при выполнении вычислений, сравнивать числа |
Базовый |
С выбором верного ответа из нескольких вариантов |
2 |
1 балл |
|
3 |
2.4.3 |
Числа и дроби |
оценивать значение квадратного корня из положительного целого числа, сравнивать числа |
Базовый |
С выбором верного ответа из нескольких вариантов |
3 |
1 балл |
|
4 |
3.1.3 |
Уравнения и неравенства |
Решать квадратные уравнения |
Базовый |
Со свободным, кратким однозначным ответом |
1 |
1 балл |
|
5 |
3.2.4 |
Уравнения и неравенства |
решать системы несложных линейных неравенств |
Базовый |
Со свободным, кратким однозначным ответом |
2 |
1 балл |
|
6 |
4.2.4 |
Функции |
Решать задачи на прогрессии с использованием формул |
Базовый |
Со свободным, кратким однозначным ответом |
3 |
1 балл |
|
7 |
2.1.4 |
Тождественные преобразования |
выполнять несложные преобразования дробно-линейных выражений, вычислять значение выражения по заданным значениям переменных |
Базовый |
Со свободным, кратким однозначным ответом |
3 |
1 балл |
|
8 |
5.1.7 |
Функции |
По графику квадратичной функции определять знаки коэффициентов b и c. |
Базовый |
С установлением соответствия |
2 |
1 балл |
|
9 |
5.1.7 |
Функции |
Находить наибольшее и наименьшее значение квадратичной функции |
Базовый |
Со свободным, кратким однозначным ответом |
2 |
1 балл |
|
10 |
3.3.2 |
Текстовые задачи |
читать информацию, представленную в виде таблицы, решать несложные текстовые задачи |
Базовый |
С выбором верного ответа из нескольких вариантов |
3 |
1 балл |
|
11 |
8.1.1 |
Статистика и теория вероятности |
читать информацию, представленную в виде таблицы, определять основные статистические характеристики числовых наборов |
Базовый |
Со свободным, кратким однозначным ответом |
3 |
1 балл |
|
12 |
8.2.1 |
Статистика и теория вероятности |
Находить вероятность события в простейших случаях |
Базовый |
Со свободным, кратким однозначным ответом |
3 |
1 балл |
|
13 |
8.2.1 |
Статистика и теория вероятности |
Находить вероятность события в простейших случаях |
Базовый |
Со свободным, кратким однозначным ответом |
3 |
1 балл |
|
14 |
3.1.4 |
Уравнения и неравенства |
Решать дробно-рациональные уравнения с отбором корней по области допустимых значений |
Повышенный |
С развернутым ответом |
5 |
2 балла |
|
15 |
3.3.2 |
Текстовые задачи |
решать задачи на движение, связывающих три величины, выделять эти величины и отношения между ними |
Повышенный |
С развернутым ответом |
15 |
2 балла |
|
16 |
3.1.3 |
Уравнения и неравенства |
Решать квадратное уравнение с параметром, исследовать квадратное уравнение |
Повышенный |
С развернутым ответом |
10 |
2 балла |
|
|
|
|
|
|
|
60 мин |
18 баллов |
Вариант I
1 часть
В каждом задании первой части необходимо записать верный ответ, в отведенном для этого месте. Каждый верный ответ оценивается в один балл.
1. Для каждого выражения укажите его значение:
А) ![]()
Б) ![]() ;
;
В) ![]() ;
;
1) 0,6; 2) 6; 3) ![]() ; 4) 1,5.
; 4) 1,5.
Ответ:
|
А |
Б |
В |
|
|
|
|
2. На координатной прямой отмечены числа a и b. Какое из следующих чисел наибольшее?

1) ![]() ;
;
2) ![]() ;
;
3) ![]() ;
;
4) ![]() ;
;
Ответ:________________
3. Запишите числа ![]() в порядке возрастания.
в порядке возрастания.
1) ![]() ;
;
2) ![]() ;
;
3) ![]() ;
;
4) ![]() ;
;
Ответ: _______________
4. Найдите корни
уравнения ![]() , в ответ запишите сумму корней уравнения.
, в ответ запишите сумму корней уравнения.
Ответ: ________________
5. Решите систему
неравенств ![]() , в ответ запишите наибольшее целое число,
удовлетворяющее системе неравенств.
, в ответ запишите наибольшее целое число,
удовлетворяющее системе неравенств.
Ответ: _________________
6. Дана
геометрическая прогрессия ![]() . Найдите сумму первых пяти ее членов.
. Найдите сумму первых пяти ее членов.
Ответ: _________________
7. Упростите
выражение: ![]() и вычислите его значение при
и вычислите его значение при ![]() .
.
Ответ: _________________
8. Установите
соответствие между графиками квадратичной функции ![]() и знаками коэффициентов b и с:
и знаками коэффициентов b и с:
9. 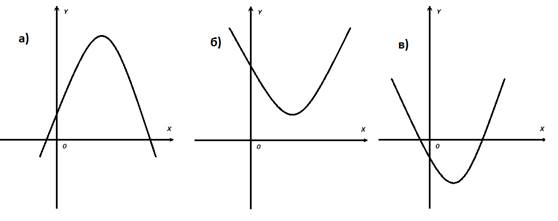
1)![]() ; 2)
; 2)![]() ; 3)
; 3)![]() ; 4)
; 4)![]()
Ответ:
|
а |
б |
в |
|
|
|
|
10. Найдите наибольшее значение функции
![]() .
.
Ответ: __________________
11. Население Челябинской области
составляет ![]() человек, а площадь Челябинской области
равна
человек, а площадь Челябинской области
равна ![]() . Сколько в среднем приходиться жителей на
. Сколько в среднем приходиться жителей на
![]() ?
?
1) Примерно 4;
2) Примерно 40;
3) Примерно 400;
4) Примерно 4000;
Ответ:__________________
12. В таблице приведены размеры некоторых озер Челябинской области:
|
№ |
Название озера |
Площадь озера (км2) |
|
1 |
Калды |
17,9 |
|
2 |
Тургояк |
26,38 |
|
3 |
Еловое |
3,12 |
|
4 |
Касарги |
14,5 |
|
5 |
Аргазинское водохранилище |
102 |
|
6 |
Чебаркуль |
19,8 |
|
7 |
Кумкуль |
5,9 |
|
8 |
Увильды |
196 |
Во сколько раз площадь озера Еловое меньше самого большого из озер указанных в таблице? (Ответ округлите до десятых).
Ответ: _________________
13. Вася наугад ставит точку на карте Челябинской области. Какова вероятность, что Вася поставит точку на территории Аргаяшского района, если его площадь равна 2683 км2 , а площадь Челябинской области равна 88300 км2? (Ответ округлите до сотых).
Ответ: __________________
2 часть
Для записи решений и ответов каждого задания второй части используйте тетрадные листы в клетку. Запишите номер выполняемого задания, затем полное обоснованное решение и ответ. Каждое задание второй части оценивается от нуля до двух баллов.
14. Решите уравнение: ![]() ;
;
15. Мотоциклист задержался с выездом на 9 минут. Чтобы наверстать упущенное время, он увеличил намеченную скорость на 10 км/ч. С какой скоростью ехал мотоциклист, если весь путь равен 30 км?
16. Найдите коэффициент а в
уравнении прямой ![]() , имеющей с параболой
, имеющей с параболой ![]() единственную общую точку.
единственную общую точку.
Вариант II
1 часть
В каждом задании первой части необходимо записать верный ответ, в отведенном для этого месте. Каждый верный ответ оценивается в один балл.
1. Для каждого выражения укажите его значение:
А) ![]()
Б) ![]() ;
;
В) ![]() ;
;
1) ![]() ; 2) 3;
3)
; 2) 3;
3) ![]() ; 4) 14.
; 4) 14.
Ответ:
|
А |
Б |
В |
|
|
|
|
2. На координатной прямой отмечены числа a и b. Какое из следующих чисел наименьшее?
![]()
1)
![]() ;
;
2)
![]() ;
;
3)
![]() ;
;
4)
![]() ;
;
Ответ: __________________
3.
Запишите
числа ![]() в порядке возрастания.
в порядке возрастания.
1)
![]()
2)
![]() ;
;
3)
![]()
4)
![]() ;
;
Ответ: ___________________
4. Найдите корни
уравнения ![]() , в ответ запишите произведение корней
уравнения.
, в ответ запишите произведение корней
уравнения.
Ответ: ____________________
5. Решите систему
неравенств ![]() , в ответ запишите наименьшее целое число,
удовлетворяющее системе неравенств.
, в ответ запишите наименьшее целое число,
удовлетворяющее системе неравенств.
Ответ: ____________________
6. Дана
геометрическая прогрессия ![]() . Найдите сумму первых пяти ее членов.
. Найдите сумму первых пяти ее членов.
Ответ: ____________________
7. Упростите
выражение: ![]() и вычислите его значение при
и вычислите его значение при ![]() .
.
Ответ: ____________________
8. Установите
соответствие между графиками квадратичных функций ![]() и знаками коэффициентов b и с:
и знаками коэффициентов b и с:
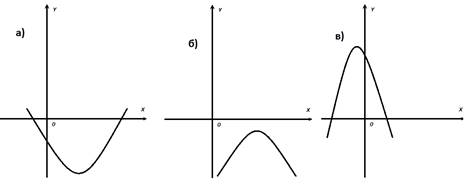
1)![]() ; 2)
; 2)![]() ; 3)
; 3)![]() ; 4)
; 4)![]()
Ответ:
|
а |
б |
в |
|
|
|
|
9.
Найдите
наименьшее значение функции ![]() .
.
Ответ: _____________________
10.
Население
Свердловской области составляет ![]() человек, а площадь Свердловской области
равна
человек, а площадь Свердловской области
равна ![]() . Сколько в среднем приходиться жителей на
. Сколько в среднем приходиться жителей на
![]() ?
?
1) Примерно 2;
2) Примерно 20;
3) Примерно 200;
4) Примерно 2000;
Ответ: _____________________
11. В таблице приведены размеры некоторых озер Челябинской области:
|
№ |
Название озера |
Площадь озера (км2) |
|
1 |
Калды |
17,9 |
|
2 |
Тургояк |
26,38 |
|
3 |
Еловое |
3,12 |
|
4 |
Касарги |
14,5 |
|
5 |
Аргазинское водохранилище |
102 |
|
6 |
Чебаркуль |
19,8 |
|
7 |
Кумкуль |
5,9 |
|
8 |
Увильды |
196 |
Во сколько раз площадь озера Увильды больше самого меньшего из озер указанных в таблице? (Ответ округлите до десятых).
Ответ: ___________________
12. Оля наугад ставит точку на карте Челябинской области. Какова вероятность, что Оля поставит точку на территории Карталинского района, если его площадь равна 4727 км2 , а площадь Челябинской области равна 88300 км2? (Ответ округлите до сотых).
Ответ: ___________________
2 часть
Для записи решений и ответов каждого задания второй части используйте тетрадные листы в клетку. Запишите номер выполняемого задания, затем полное обоснованное решение и ответ. Каждое задание второй части оценивается от нуля до двух баллов.
13. Решите уравнение: ![]() ;
;
14. Катер должен был пройти 36 км за определенный срок, но был задержан с отправлением на 18 минут. Чтобы прибыть вовремя, катер шел со скоростью, на 6 км/ч большей, чем предполагалось по расписанию. С какой скоростью шел катер?
15. Найдите
коэффициент а в уравнении параболы ![]() , имеющей с прямой
, имеющей с прямой ![]() единственную
общую точку.
единственную
общую точку.
Инструкция по проверке и оценке работ
|
№ задания |
Планируемый результат |
Правильный ответ |
Критерии оценивания / Максимальный балл |
|
|
Вариант1 |
Вариант2 |
|||
|
1 |
Выполнение действий с рациональными числами |
341 |
214 |
1 балл |
|
2 |
Сравнение рациональных чисел с использованием числового луча |
3 |
2 |
1 балл |
|
3 |
сравнение значений арифметических квадратных корней |
4 |
3 |
1 балл |
|
4 |
Решение квадратных уравнений с помощью теоремы Виета |
|
|
1 балл |
|
5 |
Решение системы линейных неравенств |
3 |
5 |
1 балл |
|
6 |
Нахождение суммы n первых чисел геометрической прогрессии |
|
|
1 балл |
|
7 |
Преобразование дробно-рациональных выражений, вычисление значения выражения при заданных значениях переменных |
|
|
1 балл |
|
8 |
Установление знаков коэффициентов b и c квадратичной функции, анализируя предложенные графики |
134 |
423 |
1 балл |
|
9 |
Вычисление наибольшего или наименьшего значения квадратичной функции |
|
9 |
1 балл |
|
10 |
Решение несложной сюжетной задачи на все арифметические действия, округление десятичных дробей |
2 |
2 |
1 балл |
|
11 |
Чтение информации, представленной в виде таблицы, определение основных статистических характеристик числовых наборов |
62,8 |
62,8 |
1 балл |
|
12 |
Вычисление геометрической вероятности события |
0,03 |
0,05 |
1 балл |
|
13 |
Решение дробно-рациональных уравнений с отбором корней по области допустимых значений |
|
|
2 балла правильно выполнены преобразования, получен верный ответ. 1 балл решение доведено до конца, но допущена ошибка вычислительного характера или описка, с ее учетом дальнейшие шаги выполнены верно. 0 баллов другие случаи, не соответствующие указанным критериям |
|
14 |
Решение текстовых задач с помощью уравнения |
50 км/ч |
12 км/ч |
2 балла получен верный обоснованный ответ. 1 балл при верных рассуждениях допущена вычислительная ошибка или описка, возможно приведшая к неверному ответу. 0 баллов другие случаи, не соответствующие указанным критериям |
|
15 |
Решение квадратного уравнения с параметром, анализ квадратного уравнения |
|
|
2 балла получен верный обоснованный ответ. 1 балл при верных рассуждениях допущена вычислительная ошибка или описка, возможно приведшая к неверному ответу. 0 баллов другие случаи, не соответствующие указанным критериям |
Геометрия 9 класс. Контрольная работа № 1 «Метод координат»
План контрольной работы
|
№ задания |
КЭС (код) |
Раздел программы (содержательная линия) |
Проверяемый планируемый результат |
Уровень сложности |
Тип задания |
Время выполнения(мин) |
Максимальный балл |
|
1 |
7.6.1 |
Векторы и координаты на плоскости
|
оперировать на базовом уровне понятиями координаты на плоскости; |
Базовый |
Со свободным, кратким однозначным ответом |
5 |
1 балл |
|
2 |
7.6.6 |
Векторы и координаты на плоскости
|
использовать векторы для решения простейших задач |
Базовый |
Со свободным, кратким однозначным ответом |
5 |
1 балл |
|
3 |
7.6.6 |
Векторы и координаты на плоскости
|
использовать векторы для решения простейших задач |
Базовый |
Со свободным, кратким однозначным ответом |
5 |
1 балл |
|
4 |
7.6.6 |
Векторы и координаты на плоскости
|
использовать координаты и векторы для решения простейших задач |
Базовый |
Со свободным, кратким однозначным ответом |
5 |
1 балл |
|
5 |
7.5.1 |
Векторы и координаты на плоскости. Уравнение прямой
|
использовать координаты и векторы для решения простейших задач |
Базовый |
Со свободным, кратким однозначным ответом |
5 |
1 балл |
|
6 |
7.6.6 |
Векторы и координаты на плоскости. Уравнение окружности
|
выполнять с помощью векторов и координат доказательство известных ему геометрических фактов и получать новые свойства известных фигур |
Повышенный |
С развернутым ответом |
7 |
2 балла |
|
7 |
7.6.6 |
Векторы и координаты на плоскости. |
выполнять с помощью векторов и координат доказательство известных ему геометрических фактов и получать новые свойства известных фигур |
Повышенный |
С развернутым ответом |
8 |
2 балла |
|
|
|
|
|
|
|
40 мин |
9 баллов |
Вариант I
1 часть
В каждом задании первой части необходимо записать верный ответ, в отведенном для этого месте. Каждый верный ответ оценивается в один балл.
8. Найдите длину
вектора![]() .
.
Ответ:______________________
9.
Даны
координаты точек А (2; 0), В ( – 1 ; 3), С (4; 6). Найдите координаты вектора ![]()
Ответ:______________________
10. Точка С (2; 1) – середина отрезка АВ, А(2; 3). Найдите координаты точки В.
Ответ:______________________
11. Найдите радиус окружности, если АВ – ее диаметр, А(1; 4), В( – 3; 7).
Ответ:______________________
12. Запишите уравнение прямой, проходящей через начало координат и точку А(2; 6).
Ответ:______________________
II часть
Для записи решений и ответов каждого задания второй части используйте тетрадные листы в клетку. Запишите номер выполняемого задания, затем полное обоснованное решение и ответ. Каждое задание второй части оценивается от нуля до двух баллов.
8.
Найдите
координаты центра и радиус окружности, заданной уравнением ![]() .
.
9. Докажите, что четырехугольник ABCD с вершинами в точках А( – 12; 6), В(0; 11), С(5; – 1) D( – 7: – 6) является квадратом.
Вариант II
1 часть
В каждом задании первой части необходимо записать верный ответ, в отведенном для этого месте. Каждый верный ответ оценивается в один балл.
1. Найдите длину
вектора ![]() .
.
Ответ:______________________
2.
Даны
координаты точек А (3; 0), В ( – 1 ; – 3), С (5; 6). Найдите координаты вектора
![]()
Ответ:______________________
3. Точка С ( – 3; – 1 ) – середина отрезка АВ, В (2; – 3 ). Найдите координаты точки А.
Ответ:______________________
4. Найдите радиус окружности, если АВ – ее диаметр, А(7; 4), В( – 3; – 6 ).
Ответ:______________________
5. Запишите уравнение прямой, проходящей через начало координат и точку С( – 5 ; 6).
Ответ:______________________
II часть
Для записи решений и ответов каждого задания второй части используйте тетрадные листы в клетку. Запишите номер выполняемого задания, затем полное обоснованное решение и ответ. Каждое задание второй части оценивается от нуля до двух баллов.
6.
Найдите
координаты центра и радиус окружности, заданной уравнением ![]() .
.
7. Докажите, что четырехугольник ABCD с вершинами в точках А( 1; 6), В(4; 2), С(0; – 1) D( – 3: 3) является ромбом.
8.
Инструкция по проверке и оценке работ
|
№ задания |
Планируемый результат |
Правильный ответ |
Критерии оценивания / Максимальный балл |
|
|
Вариант1 |
Вариант2 |
|||
|
1 |
оперировать на базовом уровне понятиями сумма и разность (двух и нескольких) векторов |
13 |
10 |
1 балл |
|
2 |
Решение задач на нахождение длины вектора |
|
|
1 балл |
|
3 |
оперировать на базовом уровне произведением вектора на число |
(2; – 1) |
( – 8 ; 1) |
1 балл |
|
4 |
Решение задач на нахождение средней линии трапеции |
2,5 |
|
1 балл |
|
5 |
применять для решения задач клетчатую сетку |
у – 3х = 0 |
у + 1,2х = 0 |
1 балл |
|
6 |
Решение задач на нахождение средней линии трапеции |
(3; – 5) R=7 |
(2; –0) R=3 |
2 балла - ход решения верный, все его шаги выполнены правильно, получен верный ответ 1 балл - ход решения верный, все его шаги выполнены правильно, но даны неполные объяснения или допущена одна вычислительная ошибка |
|
7 |
Решение задач векторным методом |
|
|
2 балла - доказательство верное, все шаги обоснованы, 1 балл - доказательство в целом верное, но содержит неточности |
Контрольная работа № 2 «Соотношения между сторонами и углами треугольника»
План контрольной работы
Перечень элементов содержания
|
Код контролируемого элемента |
Элементы содержания, проверяемые заданиями
|
|
7.2 |
Треугольник |
|
7.2.7 |
Зависимость между величинами сторон и углов треугольника |
|
7.2.10 |
Синус, косинус, тангенс острого угла прямоугольного треугольника и углов от 00 до 1800. |
|
7.2.11 |
Решение прямоугольных треугольников. Теорема косинусов и теорема синусов. Основное тригонометрическое тождество. |
Вариант I
1.
В
треугольнике АВС АВ=8 см, ![]() .
Используя теорему синусов, найдите неизвестные элементы треугольника.
.
Используя теорему синусов, найдите неизвестные элементы треугольника.
2.
В
треугольнике АВС АВ=5 см, АС=7,5 см, ![]() .Используя теорему косинусов,
найдите неизвестные элементы треугольника АВС.
.Используя теорему косинусов,
найдите неизвестные элементы треугольника АВС.
3.
![]() В сосновом бору и лесопарковой зоне города Челябинска
несколько десятков каменных карьеров. Больших, как озера, зажатые в скалах, и
маленьких. Если представить, что Челябинский сосновый бор — это огромный
зеленый ковер, то каменные карьеры на нем будут словно овалы голубого топаза. Используя данные,
указанные на рисунке, найдите ширину АВ одного из таких карьеров. В
ответе укажите целое число метров.
В сосновом бору и лесопарковой зоне города Челябинска
несколько десятков каменных карьеров. Больших, как озера, зажатые в скалах, и
маленьких. Если представить, что Челябинский сосновый бор — это огромный
зеленый ковер, то каменные карьеры на нем будут словно овалы голубого топаза. Используя данные,
указанные на рисунке, найдите ширину АВ одного из таких карьеров. В
ответе укажите целое число метров.
Вариант II
1.
В
треугольнике АВС АВ=5 см, ![]() .
Используя теорему синусов, найдите неизвестные элементы треугольника.
.
Используя теорему синусов, найдите неизвестные элементы треугольника.
2.
В
треугольнике АВС АС=0,6 дм, ![]() дм. Используя теорему
косинусов, найдите неизвестные элементы треугольника АВС.
дм. Используя теорему
косинусов, найдите неизвестные элементы треугольника АВС.
3.
![]() Используя
данные, указанные на рисунке, найдите расстояние между базами отдыха А
и В, расположенными на разных берегах озера Тургояк. В ответе укажите
целое число метров.
Используя
данные, указанные на рисунке, найдите расстояние между базами отдыха А
и В, расположенными на разных берегах озера Тургояк. В ответе укажите
целое число метров.
РЕШЕНИЕ И ОТВЕТЫ
Вариант 1
1.В
треугольнике АВС АВ=8 см, ![]() .
Используя теорему синусов, найдите неизвестные элементы треугольника.
.
Используя теорему синусов, найдите неизвестные элементы треугольника.
![]() Решение:
Решение:
По
теореме синусов ![]()
![]()
![]() ,
, ![]() см
см
![]() ,
, ![]() см
см
Ответ:
![]() ,
, ![]() см,
см, ![]() см.
см.
2.В
треугольнике АВС АВ=5 см, АС=7,5 см, ![]() .Используя теорему косинусов,
найдите неизвестные элементы треугольника АВС.
.Используя теорему косинусов,
найдите неизвестные элементы треугольника АВС.
Решение:
По
теореме косинусов ![]()
ВС2=134,28,
![]() см
см
![]()
![]()
![]()
![]()
![]()
![]()
Ответ: ![]() см,
см, ![]() ,
, ![]()
3.В
сосновом бору и лесопарковой зоне города Челябинска несколько десятков каменных
карьеров. Больших, как озера, зажатые в скалах, и маленьких. Если представить,
что Челябинский сосновый бор — это огромный зеленый ковер, то каменные карьеры
на нем будут словно овалы голубого топаза. ![]() Используя данные,
указанные на рисунке, найдите ширину АВ одного из таких карьеров. В
ответе укажите целое число метров.
Используя данные,
указанные на рисунке, найдите ширину АВ одного из таких карьеров. В
ответе укажите целое число метров.
Решение:
![]()
По
теореме синусов ![]()
![]()
![]() м
м
Ответ: 47м
Вариант 2
1.В
треугольнике АВС АВ=5 см, ![]() .
Используя теорему синусов, найдите неизвестные элементы треугольника.
.
Используя теорему синусов, найдите неизвестные элементы треугольника.
Решение:
![]()
По
теореме синусов ![]()
![]()
![]() см
см
![]()
![]() см
см
Ответ:
![]() ,
, ![]() см,
см, ![]() см
см
2.В
треугольнике АВС АС=0,6 дм, ![]() дм. Используя теорему
косинусов, найдите неизвестные элементы треугольника АВС.
дм. Используя теорему
косинусов, найдите неизвестные элементы треугольника АВС.
Решение:
По
теореме косинусов ![]()
АВ2=0,9975
![]() дм
дм
![]()
![]()
![]()
![]()
Ответ: ![]() дм,
дм, ![]() ,
, ![]()
![]() 3.Используя
данные, указанные на рисунке, найдите расстояние между базами отдыха А
и В, расположенными на разных берегах озера Тургояк. В ответе укажите
целое число метров.
3.Используя
данные, указанные на рисунке, найдите расстояние между базами отдыха А
и В, расположенными на разных берегах озера Тургояк. В ответе укажите
целое число метров.
Решение:
По
теореме косинусов ![]()
![]()
![]() м
м
Ответ: 866м
Контрольная работа № 3 «Длина окружности и площадь круга»
План контрольной работы
|
№ задания |
КЭС (код) |
Раздел программы (содержательная линия) |
Проверяемый планируемый результат |
Уровень сложности |
Тип задания |
Время выполнения (мин) |
Максимальный балл |
|
1 |
7.3.5 |
Геометрические фигуры. Правильный многоугольник
|
оперировать на базовом уровне понятиями геометрических фигур (правильный многоугольник) |
Базовый |
Со свободным, кратким однозначным ответом |
5 |
1 балл |
|
2 |
7.3.5 |
Измерения и вычисления. Правильный многоугольник
|
оперировать на базовом уровне понятиями геометрических фигур (правильный многоугольник) |
Базовый |
Со свободным, кратким однозначным ответом |
5 |
1 балл |
|
3 |
7.5.8 |
Измерения и вычисления Длина дуги. Площадь кругового сектора
|
оперировать на базовом уровне понятиями геометрических фигур (круговой сектор, круговой сегмент) |
Базовый |
Со свободным, кратким однозначным ответом |
5 |
1 балл |
|
4 |
7.5.8 |
Измерения и вычисления Площадь кругового сектора
|
оперировать на базовом уровне понятиями геометрических фигур (круговой сектор, круговой сегмент) |
Базовый |
Со свободным, кратким однозначным ответом |
5 |
1 балл |
|
5 |
7.5.8 |
Измерения и вычисления Площадь круга
|
применять формулы длины и площади круга при вычислениях |
Базовый |
Со свободным, кратким однозначным ответом |
5 |
1 балл |
|
6 |
7.5.8 |
Измерения и вычисления Площадь круга
|
оперировать представлениями о длине, площади как величинами. Применять формулы длины окружности, длины дуги окружности, площади круга и кругового сектора при решении многошаговых задач, в которых не все данные представлены явно, |
Повышенный |
С развернутым ответом |
7 |
2 балла |
|
7 |
7.5.8 |
Измерения и вычисления Площадь круга
|
выполнять с помощью векторов и координат доказательство известных ему геометрических фактов и получать новые свойства известных фигур |
Повышенный |
С развернутым ответом |
8 |
2 балла |
|
|
|
|
|
|
|
40 мин |
9 баллов |
Вариант 1
Часть 1
|
1. Найдите угол правильного двенадцатиугольника.
Ответ:_____________________ _
2.
Площадь
круга, описанного около правильного четырехугольника равна ![]() см2. Найдите
сторону четырехугольника.
см2. Найдите
сторону четырехугольника.
Ответ:______________________
3. Площадь сектора круга радиуса 22 равна 165. Найдите длину его дуги.
Ответ:______________________
4.
Площадь
кругового сектора радиуса ![]() равна
216. Найдите центральный угол кругового сектора. Ответ дайте в градусах.
равна
216. Найдите центральный угол кругового сектора. Ответ дайте в градусах.
Ответ:______________________
5. Найдите площадь кольца, ограниченного концентрическими окружностями, радиусы которых равны 9 см и 5 см.
Ответ:______________________
Часть 2
|
10. Две трубы, диаметры которых равны 10 см и 24 см, требуется заменить одной, не изменяя их пропускной способности. Каким должен быть диаметр новой трубы?
11. Радиус окружности, описанной около правильного треугольника равен 16 см. Вычислите отношение площади данного треугольника к площади круга, вписанного в данный треугольник.
Вариант 2
Часть 1
|
1. Найдите угол правильного пятнадцатиугольника.
Ответ:_____________________ _
2. Радиус окружности, описанной около правильного четырехугольника равен 5 см. Найдите площадь правильного четырехугольника.
Ответ:______________________
3. Площадь сектора круга радиуса 25 равна 175. Найдите длину его дуги.
Ответ:______________________
4.
Площадь
кругового сектора радиуса ![]() равна
24. Найдите центральный угол кругового сектора. Ответ дайте в градусах.
равна
24. Найдите центральный угол кругового сектора. Ответ дайте в градусах.
Ответ:______________________
5. Найдите площадь кольца, ограниченного концентрическими окружностями, радиусы которых равны 20 см и 16 см.
Ответ:______________________
Часть 2
|
6. Две трубы, диаметры которых равны 20 см и 24 см, требуется заменить одной, не изменяя их пропускной способности. Каким должен быть диаметр новой трубы?
7. Радиус окружности,
описанной около правильного четырехугольника равен ![]() см.
Вычислите отношение площади данного четырехугольника к площади круга,
вписанного в данный четырехугольник.
см.
Вычислите отношение площади данного четырехугольника к площади круга,
вписанного в данный четырехугольник.
Инструкция по проверке и оценке работ
|
№ задания |
Планируемый результат |
Правильный ответ |
Критерии оценивания / Максимальный балл |
|
|
Вариант1 |
Вариант2 |
|||
|
1 |
Решение задачи на нахождение угла правильного многоугольника |
1500 |
1560 |
1 балл |
|
2 |
Решение задачи на нахождение стороны, площади правильного многоугольника |
2см |
50 см2 |
1 балл |
|
3 |
Решение задач на нахождение длины дуги окружности |
15 |
14 |
1 балл |
|
4 |
Решение задачи на применение площади кругового сектора |
6
00 |
600 |
1 балл |
|
5 |
Применение формулы площади круга |
|
|
1 балл |
|
6 |
Решение задачи на применение формулы площади круга |
26 см |
10 см
|
2 балла - ход решения верный, все его шаги выполнены правильно, получен верный ответ 1 балл - ход решения верный, все его шаги выполнены правильно, но даны неполные объяснения или допущена одна вычислительная ошибка |
|
7 |
Решение задачи на применение формулы площади круга |
|
|
2 балла - ход решения верный, все его шаги выполнены правильно, получен верный ответ 1 балл - ход решения верный, все его шаги выполнены правильно, но даны неполные объяснения или допущена одна вычислительная ошибка |
Контрольная работа № 4 «Движения»
План контрольной работы
|
№ задания |
КЭС (код) |
Раздел программы (содержательная линия) |
Проверяемый планируемый результат |
Уровень сложности |
Тип задания |
Время выполнения(мин) |
Максимальный балл |
|
1 |
7.1.6 |
Перемещения. Параллельный перенос
|
распознавать движение объектов (параллельный перенос и поворот) |
Базовый |
Со свободным, кратким однозначным ответом |
5 |
1 балл |
|
2 |
7.1.6 |
Перемещения. Осевая симметрия
|
распознавать симметричные фигуры |
Базовый |
Со свободным, кратким однозначным ответом |
5 |
1 балл |
|
3 |
7.1.6 |
Перемещения. Центральная симметрия
|
распознавать симметричные фигуры |
Базовый |
Со свободным, кратким однозначным ответом |
5 |
1 балл |
|
4 |
7.1.6 |
Перемещения. Поворот
|
распознавать движение объектов (параллельный перенос и поворот) |
Базовый |
Со свободным, кратким однозначным ответом |
5 |
1 балл |
|
5 |
7.1.6 |
Перемещения. Поворот
|
распознавать движение объектов (параллельный перенос и поворот) |
Базовый |
Со свободным, кратким однозначным ответом |
5 |
1 балл |
|
6 |
7.1.6 |
Перемещения
|
строить фигуру, симметричную данной фигуре относительно оси и точки. |
Повышенный |
С развернутым ответом |
7 |
2 балла |
|
7 |
7.1.6 |
Перемещения |
строить фигуру, полученную поворотом и параллельным переносом |
Повышенный |
С развернутым ответом |
8 |
2 балла |
|
|
|
|
|
|
|
40 мин |
9 баллов |
Вариант 1
Часть 1
|
1) В какой отрезок
при параллельном переносе на вектор ![]() переходит сторона
АВ прямоугольника ABCD?
переходит сторона
АВ прямоугольника ABCD?
Ответ:_____________________ _
2) При осевой симметрии точки М и К переходят соответственно в М1 и К1. При этом МК=18 см. Найдите длину отрезка М1К1.
Ответ:______________________
3) При центральной симметрии относительно начала координат точка А(4; – 5) переходит в точку В. Найдите координаты точки В.
Ответ:______________________
4)
При
повороте вокруг точки О на 500 против часовой стрелки точка К
перешла в точку К1, а точка Р в точку Р1. ![]() . Найдите величину угла
. Найдите величину угла ![]() .
.
Ответ:______________________
5) ABCD – квадрат. В какой отрезок перейдет отрезок СВ при повороте против часовой стрелки на 900 вокруг точки О?
Ответ:______________________
Часть 2
|
6) Постройте тупоугольный треугольник АВС. Постройте треугольник А1В1С1, симметричный треугольнику АВС относительно точки А, треугольник А2В2С2, симметричный треугольнику АВС относительно прямой ВС.
7)
Постройте
прямоугольник МРКТ. Отметьте точку О – точку пересечения диагоналей. Постройте
четырехугольник М1Р1К1Т1, в который
отображается прямоугольник при параллельном переносе на вектор ![]() и четырехугольник М2Р2К2Т2,
в который отображается прямоугольник МРКТ при повороте относительно токи О на
900.
и четырехугольник М2Р2К2Т2,
в который отображается прямоугольник МРКТ при повороте относительно токи О на
900.
Вариант 2
Часть 1
|
1) В какой отрезок
при параллельном переносе на вектор ![]() переходит сторона
CD прямоугольника ABCD?
переходит сторона
CD прямоугольника ABCD?
Ответ:_____________________ _
2) При центральной симметрии точки М и К переходят соответственно в М1 и К1. При этом МК=35 см. Найдите длину отрезка М1К1.
Ответ:______________________
3) При осевой симметрии относительно оси ординат точка А(4; – 5) переходит в точку В. Найдите координаты точки В.
Ответ:______________________
4)
При
повороте вокруг точки О на 350 по часовой стрелке точка К перешла в
точку К1, а точка Р в точку Р1. ![]() . Найдите величину угла
. Найдите величину угла ![]() .
.
Ответ:______________________
5) ABCD – квадрат. В какой отрезок перейдет отрезок СВ при повороте по часовой стрелке на 900 вокруг точки О?
Ответ:______________________
Часть 2
|
6) Постройте остроугольный треугольник АВС. Постройте треугольник А1В1С1, симметричный треугольнику АВС относительно точки А, треугольник А2В2С2, симметричный треугольнику АВС относительно прямой ВС.
7) Постройте ромб
МРКТ. Отметьте точку О – точку пересечения диагоналей. Постройте четырехугольник
М1Р1К1Т1, в который отображается
ромб при параллельном переносе на вектор ![]() и четырехугольник
М2Р2К2Т2, в который отображается
ромб МРКТ при повороте относительно токи О на 900.
и четырехугольник
М2Р2К2Т2, в который отображается
ромб МРКТ при повороте относительно токи О на 900.
Инструкция по проверке и оценке работ
|
№ задания |
Планируемый результат |
Правильный ответ |
Критерии оценивания / Максимальный балл |
|
|
Вариант1 |
Вариант2 |
|||
|
1 |
распознавать движение объектов , использовать свойства движения |
CD |
ВА |
1 балл |
|
2 |
распознавать движение объектов , использовать свойства движения |
18 см |
35 см |
1 балл |
|
3 |
распознавать движение объектов , использовать свойства движения |
( – 4 ; 5) |
( – 4 ;– 5) |
1 балл |
|
4 |
распознавать движение объектов , использовать свойства движения |
750 |
1050 |
1 балл |
|
5 |
распознавать движение объектов , использовать свойства движения |
ВА |
DC |
1 балл |
|
6 |
Строить образы при выполнении осевой и центральной симметрии |
|
|
2 балла – выполнены без ошибок оба вида движений 1 балл – выполнено без ошибок одно из построений |
|
7 |
Строить образы при выполнении параллельного переноса и поворота |
|
|
2 балла – выполнены без ошибок оба вида движений 1 балл – выполнено без ошибок одно из построений |
Контрольная работа №5 (Итоговая)
Распределение заданий по разделам программ(ы)
|
№ п/п |
Раздел программы (содержательная линия) |
Количество заданий базового уровня сложности |
Количество заданий повышенного уровня сложности |
|
1. |
Геометрические фигуры |
1 |
|
|
2. |
Измерения и вычисления |
3 |
2 |
|
3 |
Векторы и координаты на плоскости |
3 |
1 |
|
|
Всего |
7 |
3 |
План диагностической работы
|
№ задания |
КЭС (код) |
Раздел программы (содержательная линия) |
Проверяемый планируемый результат |
Уровень сложности |
Тип задания |
Время выполнения (мин) |
Максимальный балл |
|
1 |
7.6.1 |
Векторы и координаты на плоскости
|
оперировать на базовом уровне понятием вектор, длина вектора |
Базовый |
Со свободным, кратким однозначным ответом |
3 |
1 балл |
|
2 |
7.3.3 |
Измерения и вычисления. Средняя линия трапеции
|
оперировать на базовом уровне понятием подобие фигур |
Базовый |
Со свободным, кратким однозначным ответом |
3 |
1 балл |
|
3 |
7.6.1 |
Векторы и координаты Длина вектора |
применять базовые тригонометрические соотношения для вычисления длин, в простейших случаях |
Базовый |
Со свободным, кратким однозначным ответом |
3 |
1 балл |
|
4 |
7.6.6 |
Векторы и координаты |
оперировать на базовом уровне понятиями координаты на плоскости |
Базовый |
Со свободным, кратким однозначным ответом |
3 |
1 балл |
|
5 |
7.5.5 |
Измерения и вычисления Площадь |
решать задачи на нахождение геометрических величин по образцам или алгоритмам. |
Базовый |
Со свободным, кратким однозначным ответом |
3 |
1 балл |
|
6 |
7.5.2 |
Измерения и вычисления. Длина окружности |
решать задачи на нахождение геометрических величин по образцам или алгоритмам. |
Базовый |
Со свободным, кратким однозначным ответом |
3 |
1 балл |
|
7 |
7.1.6 |
Геометрические фигуры |
оперировать на базовом уровне понятиями |
Базовый |
Со свободным, кратким однозначным ответом |
3 |
1 балл |
|
8 |
7.4.6 |
Измерения и вычисления. Вписанная и описанная окружность
|
применять геометрические факты для решения задач, в том числе, предполагающих несколько шагов решения |
Повышенный |
С развернутым ответом |
6 |
2 балла |
|
9 |
7.6.1 |
Векторы и координаты
|
доказывать геометрические утверждения применять геометрические факты для решения задач, в том числе, предполагающих несколько шагов решения |
Повышенный |
С развернутым ответом |
6 |
2 балла |
|
10 |
7.5.2 |
Измерения и вычисления. Длина окружности |
доказывать геометрические утверждения применять геометрические факты для решения задач, в том числе, предполагающих несколько шагов решения |
Повышенный |
С развернутым ответом |
7 |
2 балла |
|
|
|
|
|
|
|
40 мин |
13 баллов |
Вариант I
1 часть
В каждом задании первой части необходимо записать верный ответ, в отведенном для этого месте. Каждый верный ответ оценивается в один балл.
1.
В
квадрате ABCD сторона
равна ![]() . Найдите длину вектора
. Найдите длину вектора ![]() .
.
Ответ:______________________
2. Средняя линия трапеции равна 15, меньшее основание равно 7. Найдите большее основание.
Ответ:______________________
3. Найдите
длину вектора ![]()
Ответ:______________________
4. Концы отрезка АВ имеют координаты А(7; 12), В(16; – 6 ) Найдите ординату точки С – середины этого отрезка.
Ответ: ___________________________
5. В параллелограмме
стороны равны 8 и ![]() . Острый угол
равен 450. Найдите площадь параллелограмма.
. Острый угол
равен 450. Найдите площадь параллелограмма.
Ответ: ___________________________
6.
Длина
окружности равна ![]() . Найдите радиус
этой окружности.
. Найдите радиус
этой окружности.
Ответ: _______________________
7. Укажите номера верных утверждений.
1) Параллелограмм имеет две оси симметрии;
2) Любой треугольник имеет центр симметрии;
3) Каждый диаметр окружности является ее осью симметрии;
4) Правильный треугольник не имеет центра симметрии.
Ответ:______________________
II часть
Для записи решений и ответов каждого задания второй части используйте тетрадные листы в клетку. Запишите номер выполняемого задания, затем полное обоснованное решение и ответ. Каждое задание второй части оценивается от нуля до двух баллов.
8. Правильный четырехугольник с периметром, равным 16, вписан в окружность. Найдите площадь круга, ограниченного этой окружностью.
9. Дан треугольник АВС с координатами вершин: А (6; 8), В (4; 2), С (0; 6). Вычислите косинус угла С.
10.
Самое
удачное колесо обозрения для беглого знакомства с достопримечательностями
Челябинска находится на берегу реки Миасс. С его высоты видно весь центр
города — краеведческий музей, Кировку, набережную, Алое поле. Высота
колеса обозрения 73 метра. За 11 минут кабина делает полный круг. Найдите
скорость движения кабины колеса обозрения. Число ![]() .
Ответ округлите до целых и выразите в км/ч.
.
Ответ округлите до целых и выразите в км/ч.
Вариант II
1 часть
В каждом задании первой части необходимо записать верный ответ, в отведенном для этого месте. Каждый верный ответ оценивается в один балл.
1. В прямоугольнике ABCD АВ=12, ВС=5. Найдите длину вектора BD.
Ответ:______________________
2. Средняя линия трапеции равна 12, большее основание 18. Найдите меньшее основание.
Ответ:______________________
3. Найдите
длину вектора ![]()
Ответ:______________________
4. Концы отрезка АВ имеют координаты А(8; 12), В(16; 9). Найдите абсциссу точки С – середины этого отрезка.
Ответ: ___________________________
5. В параллелограмме
стороны равны 12 и ![]() . Острый угол
равен 600. Найдите площадь параллелограмма.
. Острый угол
равен 600. Найдите площадь параллелограмма.
Ответ: ___________________________
6.
Длина
окружности равна ![]() . Найдите радиус
этой окружности.
. Найдите радиус
этой окружности.
Ответ: _______________________
7. Укажите номера верных утверждений.
1) Параллелограмм имеет центр симметрии;
2) Любой треугольник имеет ось симметрии;
3) Центр окружности является ее центром симметрии;
4) Правильный треугольник не имеет осей симметрии.
Ответ:______________________
II часть
Для записи решений и ответов каждого задания второй части используйте тетрадные листы в клетку. Запишите номер выполняемого задания, затем полное обоснованное решение и ответ. Каждое задание второй части оценивается от нуля до двух баллов.
8.
Правильный
четырехугольник со стороной, равной ![]() ,
вписан в окружность. Найдите площадь круга, ограниченного этой окружностью.
,
вписан в окружность. Найдите площадь круга, ограниченного этой окружностью.
9. Дан треугольник АВС с координатами вершин: А (2; 2), В (1; 2), С (4; 1). Вычислите косинус угла В.
10. Самое
новое колесо обозрения в Челябинске расположено на парковке рядом
с ТРК «Горки». Специального названия у него до сих пор нет,
но в народе его уже так и называют — колесо у «Горок».
Высота колеса обозрения 50 метров. За 14 минут кабина делает полный
круг. Найдите скорость движения кабины колеса обозрения. Число ![]() . Ответ округлите до целых и
выразите в км/ч.
. Ответ округлите до целых и
выразите в км/ч.
Инструкция по проверке и оценке работ
|
№ задания |
Планируемый результат |
Правильный ответ |
Критерии оценивания / Максимальный балл |
|
|
Вариант 1 |
Вариант 2 |
|||
|
1 |
Решение задачи на нахождение длины вектора, теорему Пифагора |
4 |
13 |
1 балл |
|
2 |
Решение задачи на свойство средней линии трапеции |
23 |
6 |
1 балл |
|
3 |
Решение задачи на нахождение длины вектора по координатам |
5 |
13 |
1 балл |
|
4 |
Решение задачи на применение формулы вычисления координат середины отрезка |
3 |
12 |
1 балл |
|
5 |
Решение задачи на нахождение площади параллелограмма по формуле |
48 |
36 |
1 балл |
|
6 |
Применение формулы длины окружности |
9 |
4,5 |
1 балл |
|
7 |
Анализ геометрических высказываний. |
34 |
13 |
1 балл |
|
8 |
Решение задачи на нахождение площади |
|
|
2 балла - ход решения верный, все его шаги выполнены правильно, получен верный ответ 1 балл - ход решения верный, все его шаги выполнены правильно, но даны неполные объяснения или допущена одна вычислительная ошибка |
|
9 |
Решение задачи с применением формулы скалярного произведения |
|
|
2 балла - ход решения верный, все его шаги выполнены правильно, получен верный ответ 1 балл - ход решения верный, все его шаги выполнены правильно, но даны неполные объяснения или допущена одна вычислительная ошибка |
|
10 |
Решение задачи на нахождение длины окружности |
1,2 км/ч |
0,66 км/ч |
2 балла - ход решения верный, все его шаги выполнены правильно, получен верный ответ 1 балл - ход решения верный, все его шаги выполнены правильно, но даны неполные объяснения или допущена одна вычислительная ошибка |
Скачано с www.znanio.ru
© ООО «Знанио»
С вами с 2009 года.
![]()


