Пакет JASP. Классическая и Байесовская модели линейной регрессии и их построение в модулях Regression и R

Термин "регрессия" (лат. - "regression" - отступление, возврат к чему-либо) введен английским психологом и антропологом Фрэнсисом  Гальтпном и связан только со спецификой одного из первых конкретных примеров, в котором это понятие было использовано.

Регрессионный анализ — раздел математической статистики и машинного обучения. Регрессионный анализ — метод моделирования измеряемых данных и исследования их свойств. Данные состоят из пар значений зависимой переменной (переменной отклика) и независимой переменной (объясняющей переменной). Регрессионная модель есть функция независимой переменной и параметров с добавленной случайной переменной.

Предполагается, что зависимая переменная есть сумма значений некоторой модели и случайной величины. Относительно характера распределения этой величины делаются распределения, называемые гипотезой порождения данных.

Линейная регрессия – одна из важнейших и часто используемых техник регрессии. Одним из достоинств этого метода является лёгкость интерпретации результатов.

Регрессия — способ выбрать из семейства функций ту, которая минимизирует функцию потерь. Последняя характеризует насколько сильно пробная функция отклоняется от значений в заданных точках. Если точки получены в эксперименте, они неизбежно содержат ошибку измерений, поэтому разумнее требовать, чтобы функция передавала общую тенденцию, а не точно проходила через все точки. В некотором смысле регрессия — это «интерполирующая аппроксимация»: мы хотим провести кривую как можно ближе к точкам и при этом сохранить ее максимально простой. За баланс между этими противоречивыми желаниями отвечает функция потерь.

Линейная регрессия

Семейство функций, из которых мы выбираем, представляет собой линейную комбинацию наперед заданных базисных функций

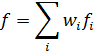
Цель регрессии — найти коэффициенты этой линейной комбинации, и тем самым определить регрессионную функцию . Линейную регрессию называют линейной из-за линейной комбинации базисных функций.

В регрессионном анализе входные переменные называются также предикторными переменными или регрессорами, а зависимые переменные — критериальными.

Если рассматривается зависимость между одной входной и одной выходной переменными, то имеет место простая линейная регрессия. Для этого определяется уравнение регрессии и строится соответствующая прямая, известная как линия регрессии.

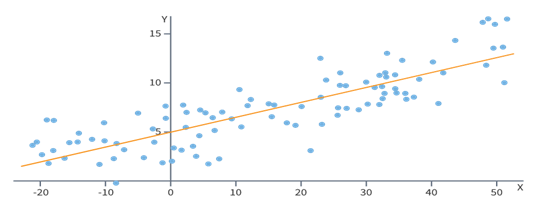
Коэффициенты a и b, называемые также параметрами модели, определяются таким образом, чтобы сумма квадратов отклонений точек, соответствующих реальным наблюдениям данных, от линии регрессии была бы минимальной. Коэффициенты обычно оцениваются методом наименьших квадратов.

Пакет JASP и интеграция с R

JASP - бесплатная графическая программа с открытым исходным кодом для статистического анализа, поддерживаемая Амстердамским университетом. Он разработан так, чтобы быть простым в использовании и знакомым пользователям SPSS (аббревиатура англ. «Statistical Package for the Social Sciences» — «статистический пакет для общественных наук»). Он предлагает стандартные процедуры анализа как в их классической, так и в байесовской форме. JASP обычно создает таблицы результатов и графики в стиле APA, чтобы упростить публикацию. Это способствует открытой науке за счет интеграции с Open Science Framework и воспроизводимости за счет интеграции параметров анализа в результаты. Разработка JASP финансируется несколькими университетами и исследовательскими фондами.

Основные функции:

·                     Предлагает как частотный (классический) анализ, так и байесовский анализ

·                     Динамическое обновление всех результатов

·                     Макет электронной таблицы и интуитивно понятный интерфейс перетаскивания

·                     Постепенное раскрытие информации для лучшего понимания

·                     Аннотированный вывод для передачи ваших результатов

·                     Интегрирован с Open Science Framework (OSF)

·                     Поддержка формата APA (копирование графиков и таблиц непосредственно в Word)

·                     Поддерживает множество форматов файлов: .sav, .txt, .csv, .ods и .jasp

С выпуском JASP 0.17 в меню для основных анализов была добавлена новая кнопка. В дополнение к переименованию, дублированию, удалению анализа и просмотру файла справки, пользователи JASP теперь имеют доступ к базовому вызову функции на языке R, который используется для вычисления результатов. Это дополнение является важным первым шагом на пути к более полной интеграции между JASP и R.

R пакет является расширением, созданным для решения конкретной задачи на языке R. Пакеты, без которых трудно было бы представить работу в R, включены в базовую сборку и автоматически доступны после установки R на Ваш компьютер (так называемое ядро R). Например, пакет stat позволяет проводить статистические тесты, а благодаря пакету graphics возможно построение графиков в R. Однако большинство пакетов имеют узкоспециализированное применение и для работы с ними требуется "расширить" свою библиотеку R, установив необходимый для работы пакет на свой компьютер.

С технической точки зрения, R пакет - это совокупность R функций, данных и документации к ним, собранных в единое целое по стандартной схеме. Каждый пакет должен быть протестирован на предмет ошибок и соответствий стандартам официального архива R пакетов (CRAN). В случае обнаружения несоответствий, пакет не будет принят в CRAN. Благодаря такому подходу принципы работы с любым R пакетом одинаковы, чем обуславливается простота и удобство их использования.

Практическая часть

Статистически значимыми в данных вычислениях оказались 4 величины: цены на вторичное жильё, квартиры в новостройках, землю и сдачу жилья  в аренду

В качестве зависимой переменной я взяла цены на вторичное жильё в Москве.

Зависимая переменная – это переменная в регрессии, которую нельзя изменять, её изменение является следствием влияния независимой переменной

В качестве независимой переменной я взяла цены на квартиры в новостройках, землю и сдачу жилья  в аренду

Независимая переменная – это та переменная в регрессии, которую можно изменять.

Стандартная ошибка регрессии — это среднее расстояние, на которое наблюдаемые значения отклоняются от линии регрессии.

Метод исключений

 коэф. Детерминации

Если , регрессионная кривая проходит через все экспериментальные точки.