PHY_10_14_V2_TG_The law of universal gravitation

Theoretical material for lesson

The higher you lift an object the more potential energy it has because the more work you had to do to put it there. Simple!! We even know an equation for it:

E_p = mgh

Now we have to consider a couple of problems.

First, in radial fields, g varies. So we can now longer use the above equation.

Secondly, we need to think about where E_p is zero. 

What causes objects to have potential energy?

Objects in a gravitational field have the potential to do work if they have a force acting on them.

Do objects on the Earth's surface have zero potential energy?

No - they definitely have a force on them because they don't drift away so they have the potential to do work. In fact, push them into a hole and you will see some of that energy being converted into kinetic energy.

Where is the gravitational force between objects zero?

The force between objects due to gravity reduces as the distance separating the objects increases. So the force finally becomes zero at infinity.

Going back to our GCSE ideas, at the greatest possible distance from Earth, you should have your greatest possible value of E_p. But at infinity, the attraction due to g-field is zero. No force → no potential energy.

So the greatest E_p value you can get is zero!!!! And you get it at infinity.

When you move back towards Earth from infinity, your E_p reduces. So it must become less than zero! It must become negative.

Now that's confusing! The good news is, you don't have to know exactly where infinity is to answer any questions. That'sbecause:

1.                   We are often only interested in the change in potential energy rather than the actual value.

2.                   Someone very thoughtfully came up with a way of calculating the potential energy that an object has by looking at the separation between the object and the centre of the field, rather than infinity. (Readonfortheequation.)

Rather than talking about gravitational potential energy all the time, it is useful for a number of reasons to define a new quantity - Gravitational Potential, Φ.

It is a very simple idea. Gravitational potential is the potential energy per kilogram at a point in a field. So the units are Jkg^-1, joules per kilogram.

The equation for potential is:

where

G = the universal gravitational constant

m = the mass causing the field

r = the distance between the centre of the mass causing the field and the point you are considering.

Notethat:

1. Just like potential energy, the biggest value of potential you can get is zero. All other values are less than zero - i.e. negative!!

2. Potential is not a vector even though it has a negative sign. It doesn't have a direction, only a magnitude.

Worked Example

Example

If G = 6.67x10^-11Nm²kg^-2 and the mass of the Earth is 6.0x10²⁴kg, calculate the potential at the surface of the Earth if the radius of the Earth is 6.4x10⁶m.

Answer

The potential (Ep per kg) at the surface of the Earth is

- 63 MJ kg ^-1

Do 10 MJ kg^-1 of work on raising an object from the Earth's surface and it will move up to a point where it's potential is - 53MJ kg^-1. That's 10 MJ kg^-1 greater than on the surface because it is 10MJ kg^-1 closer to zero.

Confusing! Look at the following diagram. It shows how potential drops as you move further from the surface of the Earth.

So we can define potential as "the work done per kg by an object when it moves from infinity to a point in a field".

Looking back at the example above, that means that if you let 1kg drop from infinity to the surface of the Earth it will lose 63MJ of potential energy. Ignore air resistance, and the object will have that much kinetic energy when it hits the surface of the planet.

Potential Energy Equation

The potential Φ at a point in a field is the potential energy per kg.

So, if you put a mass of 'm' kg at that point, its potential energy is:

Ep = mΦ

so, in a radial field,

EscapingVelocity

To escape completely from the Earth's gravitational field you need to give an object 63MJ of kinetic energy per kg. (As it rises from the Earth it will lose kinetic energy and gain potential energy)

This allows you to calculate an object's escape velocity - how fast you would have to throw it to get it completely out of the Earth's gravity field.

If it needs 63MJkg^-1 energy then it must start off with all this energy as Ek.

So:

 where m = 1kg

Rearrange to get:

v = 11,200 ms^-1.

That's how fast you'd have to throw it.

Equipotential

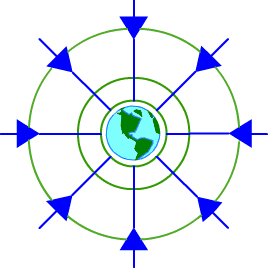
Look at any of the green lines on the diagram above. The line is drawn a distance from the centre of the Earth. The potential at any point on that dotted line is the same, calculated from:

As this is a series of points of equal potential, we call it an equipotential.

If you follow a path along an equipotential, your Ep doesn't change. Therefore you don't lose or gain energy. No work is done.

That's the theory behind why satellites can remain in space without always using energy to stay there. They follow equipotentials. It also applies to the Moon orbiting the Earth and the Earth orbiting the Sun. They all follow equipotentials (almost!).

Potential Gradient

If you draw equipotentials showing uniform, regular changes (steps) in potential i.e. an equipotential every 10MJkg^-1, you will notice that the space between them increases as you move away from the Earth.

This shows that the potential changes more rapidly for changes in height near the Earth than for changes of height a long distance away from the Earth.

In fact, it can be shown that:

Potential gradient = gravitational field strength, g.

Or, for the mathematicians amongst you:

Differentiation task

This question is about electric and gravitational fields

(a)               State, in terms of electrons, the difference between a conductor and an insulator.

............................................................................................................................................................................................................................................................................(1)

 (b)              Suggest why there must be an electric field inside a current-carrying conductor.

..............................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................(3)

(c)               The magnitude of the electric field strength inside a conductor is 55 N C–1. Calculate the force on a free electron in the conductor.

............................................................................................................................................................................................................................................................................(1)

(d)               The electric force between two point charges is a fundamental force as is the gravitational force between two point masses. State one similarity between these two forces and one difference (other than the fact that one applies to charge and the other to mass).

Similarity: .........................................................................................................................................................................................................................................................

Difference: ........................................................................................................................................................................................................................................................(2)

(e)               The force on a mass of 1.0 kg falling freely near the surface of Jupiter is 25 N. The radius of Jupiter is 7.0 × 107 m.

(i)                         State the value of the magnitude of the gravitational field strength at the surface of Jupiter.

...........................................................................................................................(1)

 (ii)                       Calculate that the mass of Jupiter is about 1.8 × 1027 kg.

.......................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................

(2)

(Total 10 marks)

Mark scheme

(a)     a conductor contains “free” electrons and insulators do not / OWTTE;                             1

 (b)    to have a current electrons must be accelerated/move along the wire;
and so a (electric) force must act on them;
this is provided by the electric field;                                                                    3

 (c)    8.8 × 10–18 N;                                                                                                    1

 (d)    similarity:
both follow an inverse square law;

          difference:
gravitational force is always attractive/is much weaker than electric
force / electric force can be repulsion/is much stronger than
gravitational force;                                                                                             2

 (e)    (i)      25 N kg–1;                                                                                                1

 (ii)    M= ;
= ;
=1.8 × 1027 kg                                                                                          2

[10]