PHY_10_37_V1_DM_Capacitors

What is a capacitor? How does it made up?

Capacitors are very interesting and very useful circuit elements. They can store charge, discharge it rapidly (or more slowly if used in combination with resistors), and they can essentially block direct current.

They can be used in timing circuits, filtering circuits ... all kinds of things. Rapid chargers in electric cars employ capacitors to store charge rapidly and introduce it to the batteries more slowly later.

Form of a capacitor

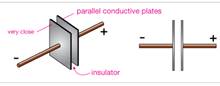
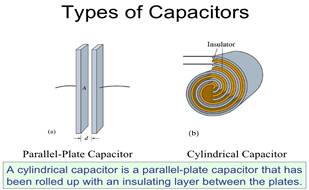
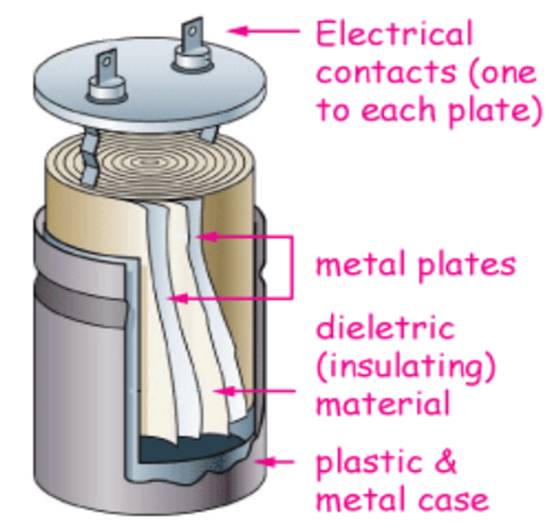
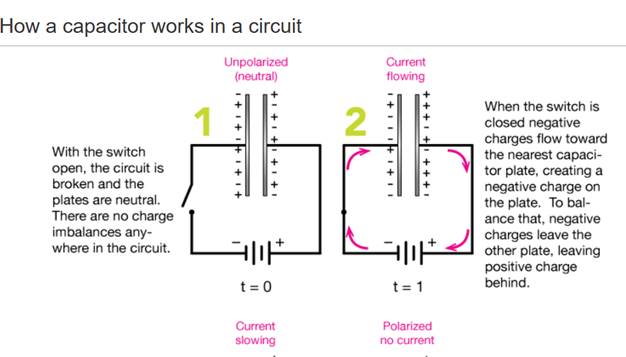
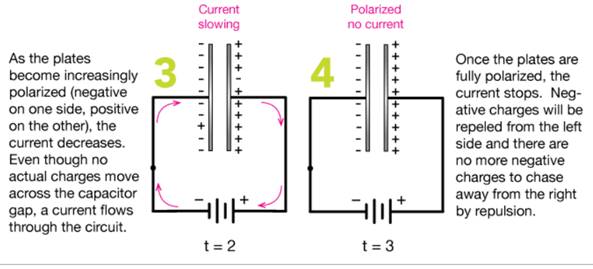
A capacitor is really pretty simple. A Capacitor is a two parallel plates, separated by air or some other insulator.

The plates must be pretty close together, often just the with of a thin plastic film.. Each plate is connected to a conductor which connects into a circuit.

 

 

 

 

 

 

Unit of capacitance

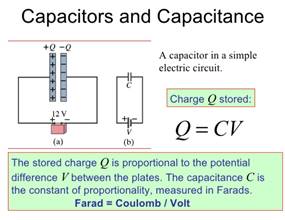
The unit of capacitance is the Farad (F), named after Michael Faraday. The base units of the Farad are, 1 F = s⁴·A²·m^-2·Kg^-1. That's not often too helpful. The most useful conversion we can make (and there are a lot of them) is that 1 F = 1 C/V; One Farad is one coulomb of charge per volt of potential.

In practice, one Farad (1F) is a very large amount of capacitance.

Charge a 1 F capacitor up and touch it and you'll get the shock of your life (maybe your last). In electronics applications, units of microfarads (1 μF = 10^-6 F), nanofarads (1 nF = 10^-9 F) or picofarads (1 pF = 10^-12 F) are much more common. Pictured above is a 68 μF capacitor that can be held at a potential of up to 100 V before the insulator between the plates breaks down and allows current to flow.

Capacitance depends on geometry and insulation

The amount of capacitance (capacity to hold charge) of such a device is dependent on three things:

1.    The area of overlap of the two parallel plates, A

2.    The distance between the plates, d

3.    The nature of the material in between the plates, which cannot be a conductor.

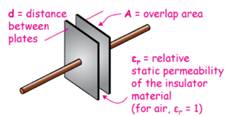
The two geometric properties, A & d, aren't difficult to figure out. The quality of insulation between the plates is ranked with a number, ε_r, called the relative static permeability. ε_r = 1 for air and can range from 1 for a vacuum (we actually define ε_r = 1 for a vacuum) to over 12,000 for an inorganic compound called calcium copper titanate.

Mathematically, capacitance scales linearly with overlap area and ε_r, and inversely with the distance between plates:

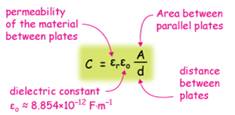
It's easy to see that as we increase either the area of overlap of the plates or the quality of the insulation material, and as we decrease the the distance between plates, we increase the capacitance of the device. The constant ε_o in the capacitance formula is called the dielectric constant, ε_o = 8.754 x 10^-12 F/m, and it's there, like any proportionality constant in physics, to get the units right.

In capacitors, we'd like to have

• small inter-plate distances,
• large areas of overlap between parallel plates, and
• a separating material with a very high permittivity value*.

*Note that the word "permittivity" here is the opposite of what we really mean. High-permittivity substances really do not "permit" the flow of current very well. It's an old term we're kind of stuck with

Uses of Capacitors

 

Uses of Capacitors

 

 

Problem Solving Capacitor and capacitance

1.    A capacitor that has air between its plates is connected across a potential difference of 12.0V and stores 48.0mC of charge. What is the capacitance of the capacitor? Give your answer in μF

2.    We have a parallel plate capacitor constructed of two parallel plates, each with area  separated by a distance of 1.00mm. What is the capacitance of this parallel plate capacitor?

3.    What happens to the capacitance of the parallel plate capacitor if increase the distance between plated by the factor of 3?

4.    A parallel plate capacitor with air between the plates has a capacitance of 8pF. What will be the capacitance if the distance between the plates is reduced by half, and the space between them is filled with a dielectric (dielectric constant=6)?

5.    A parallel - plate capacitor has a plate separation of 1.00mm and a capacitance of 1.00F. Find the area of the plates.

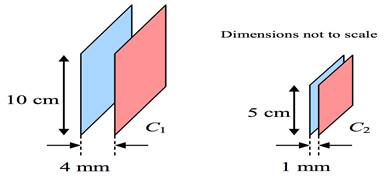
6.    Capacitor C1 consists of square parallel plates 10cm on side, and separated by a distance 4mm, as shown in the figure.  Capacitor C2 has square parallel plates 5cm on a side, and separated by a distance of 1mm. What is a ratio between the capacitances of two parallel-plate systems?

 

Скачано с www.znanio.ru