PHY_10_V1_DM_Revision term 1

Kinematics:

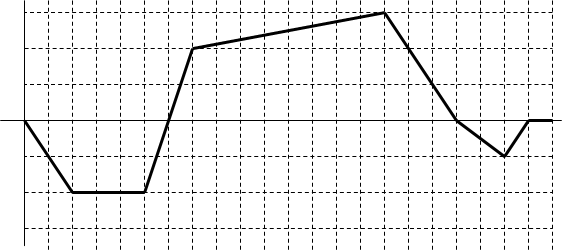1.       The graph below describes the motion of a fly that starts out going right.


          15.0

V(m/s 10.0

             5.0

                                              5                            10                           15                         20             time (s)

           -5.0 

         -10.0

         -15.0

a.       Identify section(s) where the fly moves with constant velocity

b.      Identify section(s) where the fly moves right slowing down

c.       Identify section(s) where the fly moves left speeding up

d.      When is the fly at rest?

e.       What is the average velocity of the fly between 0 and 15 seconds?

f.        What is the distance traveled by the fly in this time interval?

g.      What is the average speed of the fly in the same time interval?

h.      What is the average acceleration of the fly in this time interval?

i.        What is the total displacement of the fly from 0 to 22 seconds?

j.        Identify the times when the fly changes direction.

k.      Draw an acceleration vs. time graph for the fly.

Dynamics:

1.      Is the earth’s gravitational force on the sun larger than, smaller than, or equal to the sun’s gravitational force on the earth? Explain.

2.      The gravitational force of a star on orbiting planet 1 is F1. Planet 2, which is twice as massive as planet 1 and orbits at twice the distance from the star, experiences gravitational force F2. What is the ratio F1/F2?

3.      A 1000 kg satellite and a 2000 kg satellite follow exactly the same orbit around the earth.

a.       What is the ratio F1/F2 of the gravitational force on the first satellite to that on the second satellite?

b.      What is the ratio a1/a2 of the acceleration of the first satellite to that of the second satellite?

4.      How far away from the earth must an orbiting spacecraft be for the astronauts inside to be weightless?

Momentum:

1.      A 1500-kg satellite orbits a planet in a circular orbit of radius 6.2 * 10⁶ m. What is the angular momentum of the satellite in its orbit around the planet if the satellite completes one orbit every 1.5 * 10⁴ s?

(a)    3.9 * 10⁶ kg × m²/s             (c)  6.2 * 10⁸ kg × m²/s             (e)  2.4 * 10¹³ kg × m²/s

(b)   1.4 * 10¹⁴ kg × m²/s           (d) 8.1 * 10¹¹ kg × m²/s

(b)

2.      A 60.0-kg skater begins a spin with an angular speed of 6.0 rad/s.  By changing the position of her arms, the skater decreases her moment of inertia by 50 %.  What is the skater's final angular speed?

2.(a)  3.0 rad/s                            (c)  9.0 rad/s                            (e)  18 rad/s

2.(b)  4.5 rad/s                            (d) 12 rad/s 

3. 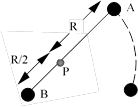     Two equal spheres, labeled A and B in the figure, are attached to a massless rod with a frictionless pivot at the point P.  The system is made to rotate clockwise with angular speed w on a horizontal, frictionless tabletop.  Sphere A collides with and sticks to another equal sphere that is at rest on the tabletop.  Note: the masses of all three spheres are equal.  What is the angular speed of the system immediately after the collision?

3.(a)  w                                       (c)  0.60w                                (e)  0.29w

3.(b)  0.82w                                (d)  0.56w

4.      Planets A and B are uniform solid spheres that rotate at a constant speed about axes through their centers.  Although B has twice the mass and three times the radius of A, each planet has the same rotational kinetic energy.  What is the ratio VB/VA of their angular speeds?

4.(a)  0.055                                 (c)  0.165                                 (e)  0.236

4.(b)  0.093                                 (d) 0.191

5.      A solid sphere of radius R rotates about a diameter with an angular speed w.  The sphere then collapses under the action of internal forces to a final radius R/2.  What is the final angular speed of the sphere?

(a)   w/4                                    (c)  w                     (e)              4w

(b)   w/2                                    (d)  2w

6. 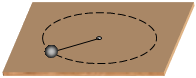     A ball of mass M moves in a circular path on a horizontal, frictionless surface.  It is attached to a light string that passes through a hole in the center of the table.  If the string is pulled down, thereby reducing the radius of the path of the ball, the speed of the ball is observed to increase.  Complete the following sentence:  This occurs because

(a)    the linear momentum of the ball is conserved.

(b)   it is required by Newton's first law of motion.

(c)    the angular momentum of the ball is conserved. 

(d)   the angular momentum of the ball must increase.

(e)    the total mechanical energy of the ball must remain constant.

7. 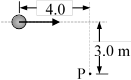     A 3.0-kg ball moves in a straight line at 10 m/s as shown in the figure.  At the instant shown, what is its angular momentum about the point P?

(a)    30 kg × m²/s                       (d) 150 kg × m²/s

(b)   90 kg × m²/s                       (e)  zero kg × m²/s

(c)    120 kg × m²/s

Mechanics of liquids and gases:

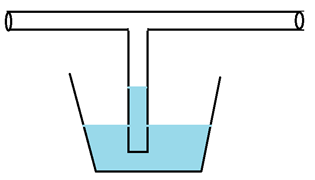
1.      In the figure at right, how does v₁, the velocity of the air in the tube, compare to v₂, the velocity of the air outside the tube?  

a.       v₁< v₂

b.      v₁> v₂

c.       v₁= v₂

2.      A sump pump (used to drain water from the basement of houses built below the water table) is draining a flooded basement at the rate of 0.750 L/s, and pumps water into a hose at a pressure of 3.00×10⁵N/m².

a.       The water enters a hose with a 3.00-cm inside diameter and rises 2.50 m above the pump. What is its pressure at this point?

b.      The hose goes over the foundation wall, losing 0.500 m in height, and widens to 4.00 cm in diameter. What is the pressure now? Assume the water in the hose behaves like an ideal liquid.

3.      A barrel full of rainwater has a spigot near the bottom, at a depth of 0.80 m beneath the water surface. (a) When the spigot is directed horizontally  and is opened, how fast does the water come out?

 (b) If the opening points upward, how high does the resulting “fountain” go?