
Theoretical material for the lesson, definitions for concepts
Thermal topics 3, 10 |
|
|
|
temperature, T [K] |
measure of how hot something is (it can be used to work out the direction of the natural flow of thermal energy between two objects in thermal contact) OR measure of the average K.E. of molecules it is measured on a defined scale (Celsius, Kelvin etc.) |
|
|
temperature is proportional to a measure of the average kinetic energy; of the molecules of the substance; or: idea that temperature shows natural direction of the flow of thermal energy; from high to low temperature / OWTTE; (do not accept ìhot to coldî) [2] Award [1 max] for a rough and ready answer and [2 max] for a more detailed answer. |
|
|
|
thermal energy |
thermal energy is the KE of the component particles of an object thus measured in joules |
|
|
heat, Q [J] |
energy transferred from one body to another due to a temperature difference |
|
|
thermal equilibrium |
2 bodies that are in thermal contact are in thermal equilibrium when the net heat flow between them is zero, therefore the 2 bodies must have the same temperature |
|
|
microscopic |
on the scale of atoms and molecules eg the microscopic properties of a gas are particle mass, velocity, kinetic energy, momentum |
|
|
macroscopic |
on the scale of people (ie what we observe) eg the macroscopic properties of a gas are temperature, volume, pressure, density |
|
|
ideal gas |
gas that obeys the equation pV = nRT / no forces between molecules; at all pressures, volumes and temperatures / any other postulate; |
|
|
obeys
the universal gas law / at all values of pressure, volume and temperature or no mutual force of attraction/repulsion; |
|
|
|
satisfies pV = nRT (at all p, V and T) / point molecules / no intermolecular forces; Allow any other kinetic theory assumption |
|
|
|
kinetic theory of gases |
a model of the microscopic behaviour of
gas particles that explains the macroscopic behaviour of the gas (ie the
ideal gas law, |
|
|
internal energy, U [J] |
· the sum of all random kinetic energies and mutual potential energies of the particles of the body or system · internal energy does not include the kinetic energy or potential energy of the body as a whole · an ideal gas has no intermolecular forces therefore the gas particles have no mutual potential energies therefore the internal energy of an ideal gas depends only on the KE of the particles (temperature of gas) |
|
|
sum of (random) kinetic (and potential energies); of the molecules of the system (allow atoms or particles); |
||
|
mole, n [mol] |
amount of substance of a system which contains as many elementary units as there are carbon atoms in 12 x 10-3 kg of carbon-12 |
|
|
molar mass |
the mass of one mole of a substance |
|
Avogadro constant, NA |
the number of atoms in exactly 12 x 10-3 kg of the nuclide carbon-12 |
|
|
specific heat capacity c [J kg-1 K-1] |
specific heat capacity is the amount of energy required to raise the temperature of unit mass through 1 K; |
|
|
quantity of thermal energy (heat) required to raise temperature of unit mass; by one degree; Award [1 max] for use of units, rather than quantities. |
|
|
|
quantity of (thermal) energy/heat required to raise temperature of unit mass; by one degree; or |
|
|
|
Heat (thermal) capacity C [J k-1] |
the amount of energy / heat required to raise the temperature of a substance / object through 1K/ C; |
|
|
the energy/heat required to raise/change the temperature of a substance by1K/ C; |
|
|
|
evaporation |
evaporation is the escape of molecules from the surface of the liquid |
|
|
boiling |
boiling occurs when molecules escape in the form of bubbles of vapour from the body of the liquid |
|
|
specific latent heat, l [J kg-1] |
energy per unit mass required to change the phase of a substance at its phase change temperature |
|
|
specific latent heat of vaporisation: quantity of thermal energy/heat required to convert unit mass / mass of 1 kg of liquid to vapour/gas; with no change of temperature / at its boiling point; |
|
|
|
pressure, p [pascal, Pa] |
the pressure experienced by a body
immersed in a fluid is the (normal) force per unit area exerted by the fluid
on the surface of the body |
|
|
indicator diagram |
graph of pressure against volume for a gas |
|
|
isochoric (isovolumetric) |
a process where the volume remains
constant, therefore there is no work done ( |
|
|
a process that takes place at constant volume |
|
|
|
isobaric |
a process where the pressure remains constant |
|
|
a process that takes place at constant pressure |
|
|
|
isothermal |
a process where the temperature remains
constant, therefore the internal energy remains constant for an ideal gas, |
|
|
change in which the temperature stays constant; |
|
|
|
adiabatic |
a process where no heat enters or leaves
the system, |
|
|
a process in which there is no energy (heat) exchange; between system and surrounding; or all the work done; either increases or decreases the internal energy of the system; |
|
|
|
a compression or expansion / change in state (of the gas); in which no (thermal) energy is exchanged between the gas and the surroundings / in which the work done is equal to the change in internal energy of the gas; |
|
|
|
work (derivation) |
force on piston = pA; where A is area of piston. Piston moves distance x; work done = pAx; Ax = V, so W = p V; |
|
|
entropy, S [J K-1] |
S [J K-1], measure of disorder of a system |
|
|
the degree of disorder (in the system) |
|
|
|
2nd law of thermodynamics |
total entropy (of the universe); is increasing; |
|
|
in any process, (reaction, event etc.) the overall entropy of the universe/a closed system increases ; |
|
|
|
total entropy of universe is increasing; |
|
|
Additional guidelines for organizing a lesson
Students can deduce topic of the lessen and objectives, for clarification you can show topic and the learning objectives on the presentation.
Then Subject-specific vocabulary & terminology will be presented to the students and their activities during the research work will be explained.
Then teacher will give the worksheet on the concepts studied previously. Students attempt the questions in groups as they engage in discussion. The teacher helps the learners with difficulties in answering the questions.
Reinforce the LO’s: answer any questions students may have/clarify understanding. Students reflect on their learning.
At the end of the lesson teacher will give homework.
Additional multilevel (on differentiation) tasks
Each chapter has extra tasks which you would use for high level students.
Recommendations for formative assessment
1) Use the answers provided to assess students’ understanding and the manner of application of the all terms concept knowledge
2) Provide a general feedback for every given point (pay attention to give a fully explained feedback to the points that were not given)
3) You can change the numbers in calculations according to the student’s ability
Answers, criteria for assignments, additional materials for the lesson
Answers:
Q1.
A
[1]
Q2.
(a)
(i) collisions with/bombardment by air molecules
(condone particles)
B1
1
(ii) motion of air
molecules (“they are“) random
(in all directions)
B1
fast moving
B1
max 2
air
molecules small or much smaller than smoke
particles
B1
(b) (i) 3/2kT or substituted values (independent of powers)
do not allow all equations written
C1
6.21 × 10–21 J
A1
2
(ii) pV = 1/3 Nm<c2>
C1
relates Nm/V to ρ
C1
2.4 × 105 m2s–2
A1
(allow compensation of ½ m<c2> for 1)
3
(iii) there will be a range of speeds
B1
there
will be molecules with lower speeds
than mean /average
means higher and lower values
B1
2
[10]
Q3.
(a)
(i) (Mass change in u=)
1.71× 10−3
(u)
or (mass Be−7) ‒ (mass He−3) ‒ (mass He−4)
seen with numbers
C1
2.84
× 10−30 (kg)
or Converts their mass to kg
Alternative
2nd mark:
Allow conversion of 1.71 × 10−3 (u) to MeV by
multiplying by 931 (=1.59 (MeV)) seen
C1
Substitution in E = mc2 condone their mass difference in this sub but must have correct value for c2 (3×108)2 or 9×1016
Alternative
3rd mark:
Allow their MeV converted to joules (× 1.6 × 10−13)
seen
C1
2.55 × 10−13 (J) to 2.6 × 10−13 (J)
Alternative
4th mark:
Allow 2.5 × 10−13 (J) for this method
A1
4
(ii) Use of E=hc / λ ecf
C1
Correct substitution in rearranged equation with λ subject ecf
C1
7.65 × 10−13 (m) to 7.8 × 10−13 (m) ecf
A1
3
(b) (i) Use of Ep formula:
C1
Correct charges for the nuclei and correct powers of 10
C1
2.6(3) × 10−13 J
A1
3
(ii) Uses KE = 3 / 2 kT: or halves KET, KE= 1.3 × 10−13 (J) seen ecf
C1
Correct
substitution of data and makes T subject ecf
Or uses KET value and divides T by 2
C1
6.35 × 109 (K) or 6.4 × 109 (K) or 6.28 × 109(K) or 6.3 × 109 (K) ecf
A1
3
(c) (i) Deuteron / deuterium / hydrogen−2
B1
Triton / tritium / hydrogen−3
B1
2
(ii) Electrical heating / electrical discharge / inducing a current in plasma / use of e−m radiation / using radio waves (causing charged particles to resonate)
B1
1
[16]
Q4.
(a)
(i) p2 = p1 (V2/V1)1.4
= 1.0 × 105 (2.1/1.2)1.4 ![]()
OR 1.0
× 105 × (2.1 × 10−5)1.4
= p2 × ((1.2 × 10-5)1.4 ![]()
p2 = 2.2
× 105 Pa ![]()
2
(ii) ![]()
![]()
OR use of p1V1 = nRT1 to find n or nR and substitute in
p2V2 = nRT2
to find T2 ![]()
T2 = 360
K ![]() 2 sig fig
2 sig fig ![]()
3
(b) (Q = W + ∆U)
Q = 0
(and W negative ) ![]()
So
∆U ( = - W) = 1.4 J ![]()
2
(c) (slow)
compression is (nearly) isothermal / at constant temperature ![]()
greater
change in volume needed to rise to same final pressure ![]()
(OR
correct p-V sketches showing adiabatic and isothermal processes
![]() )
)
hence
less / piston pushed in further ![]()
3
[10]
Q5:
Initial length of wire = L = 5 m, Strain = 1% of 0.1 = 1 × 10-2 × 0.1 = 1 × 10-3, Area of cross-section = 1 mm² = 1 × 10-6 m², Load attached = F = 10 kg-wt = 10 × 9.8 N .
Elongation = l = ?, Stress = ?,
Strain = l /L
∴ extension = l = Strain × L
∴ l = 1 × 10-3 × 5
∴ l = 5 × 10-3 m = 5 mm
Stress = F / A = mg /π r²
∴ Stress = ( 10 × 9.8) /( 1 × 10-6 )
∴ Stress = 9.8 × 107 N/m²
Ans: Extension = 5 mm and Stress = 9.8 × 107 N/m²
Q6:
Initial length of wire = L = 2 m, Radius of wire = 0.35 mm = 0.35 × 10-3 m = 3.5 × 10-4 m, Load attached = F = 4 kg wt = 4 × 9.8 N, g = 9.81 m/s² ,Y = 11 × 1010 N/m².
Extension = ?
Y = FL /A l
∴ l = F L /π r² Y
∴ l = (4 × 9.8 × 2) /(3.142 × (3.5 × 10-4)² × 11 × 1010 )
∴ l = (4 × 9.8 × 2) /(3.142 × 12.25 × 10-8 × 11 × 1010 )
∴ l = 1.85 × 10-3 m = 0.185 × 10-2 m = 0.185 cm
Ans: Extension of wire is 0.185 m
Q7: Initial length of wire = L = 1.5 m, Radius of wire = 0.4 mm = 0.4 × 10-3 m = 4 × 10-4 m, Extension = l = 1.2 mm = 1.2 × 10-3 m, g = 9.8 m/s² , Young’s modulus = Y = 12.5 × 1010 N/m².
Stretching force = F = ?
Y = FL /A l
∴ F = AY l /L
∴ F = π r² Y l /L
∴ F = (3.142 × (4 × 10-4)² × 12.5 × 1010 × 1.2 × 10-3) /1.5
∴ F = (3.142 × 16 × 10-8 × 12.5 × 1010 × 1.2 × 10-3) /1.5
∴ F = 50.27 N
Ans: Stretching force required = 50.27 N
Q8:
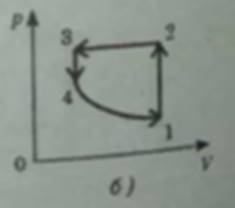
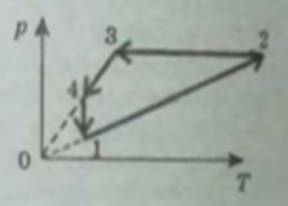
a) 1 → 2 isochoric heating
2 → 3 isobaric compression with cooling happening
3 → 4 isochoric cooling
4 → 1 isothermal expansion
List of useful links and literature
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.