PHY_10_V2_DM_Revision term 2 (1)

Fundamental principles of molecular-kinetic theory:

1.      A fixed mass of gas occupies a volume V. The temperature of the gas increases so that the root mean square velocity of the gas molecules is doubled. What will the new volume be if the pressure remains constant?

2.      Helium is a monatomic gas for which all the internal energy of the molecules may be considered to be translational kinetic energy.

molar mass of helium       =    4.0 × 10^–3 kg
the Boltzmann constant    =    1.38 × 10^–23 J K^–1
the Avogadro constant      =    6.02 × 10²³ mol^–1

(a)          Calculate the kinetic energy of a tennis ball of mass 60 g travelling at

 50 m s^–1

 (b)     Calculate the internal energy of 1.0 g of helium gas at a temperature of 48K.

(c)     At what temperature would the internal energy of 1.0 g of helium gas be equal to the kinetic energy of the ball in part (a).

3. (a)     Use the kinetic theory of gases to explain why

(i)      the pressure exerted by an ideal gas increases when it is heated at constant volume.

 (ii)     the volume occupied by an ideal gas increases when it is heated at constant pressure.

 (b)     A quantity of 0.25 mol of air enters a diesel engine at a pressure of 1.05 × 10⁵ Pa and a temperature of 27°C. Assume the gas to be ideal.

(i)      Calculate the volume occupied by the gas.

 (ii)     When the gas is compressed to one twentieth of its original volume the pressure rises to 7.0 × 10⁶ Pa. Calculate the temperature of the gas immediately after the compression.

Fundamentals of thermodynamics: 

4.      The figure below shows a theoretical engine cycle in which a fixed mass of ideal gas is taken through the following processes in turn:

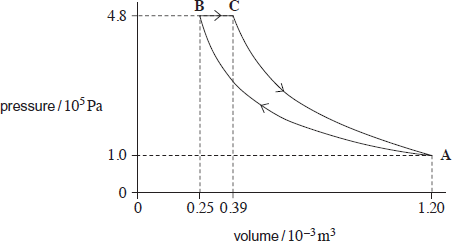
(a)     (i)      Show that process A → B is isothermal.

(ii)     Calculate the work done by the gas in process B → C.

work done ____________________ J

(b)     Complete the table. Apply the first law of thermodynamics to determine values of Q, W and ΔU for each process and for the whole cycle. Use a consistent sign convention.

(c)     The overall efficiency of an engine is defined as

Calculate the overall efficiency of the cycle.

overall efficiency ____________________

(d)     Describe two problems that would be encountered in trying to design a real engine based on this cycle.

Liquid and solid bodies:

5.      A wire 2 m long and 2 mm in diameter, when stretched by weight of 8 kg has its length increased by 0.24 mm. Find the stress, strain and Young’s modulus of the material of the wire. g = 9.8 m/s² .

6.      A wire of length 2 m and cross-sectional area 10^-4 m² is stretched by a load 102 kg. The wire is stretched by 0.1 cm. Calculate longitudinal stress, longitudinal strain and Youn’s modulus of the material of wire.

7.      A mild steel wire of radius 0.5 mm and length 3 m is stretched by a force of 49 N. calculate a) longitudinal stress, b) longitudinal strain c) elongation produced in the body if Y for steel is 2.1 × 10¹¹ N/m².

8.      A metal wire 1 m long and of 2 mm diameter is stretched by a load of 40 kg. If Y = 7 × 10¹⁰ N/m² for the metal, find the (1) stress (2) strain and (3) force constant of the material of the wire.

Gas laws:

9.      When the pressure of an ideal gas of a given mass at a temperature of  Т=273 K is P₁=10 kPa its volume V₁=20 m³.

Construct a graph of the isothermal process of this gas if the final gas pressure  P₂=4 kPa.

a on coordinate axes p-V.

b on coordinate axes V-T.

c on coordinate axes p-T.