PHY_10_V2_TG_Revision term 2 (1)

Theoretical material for the lesson, definitions for concepts 

The kinetic theory of gases describes a gas as a large number of submicroscopic particles (atoms or molecules), all of which are in constant, rapid, random motion. The randomness arises from the particles' many collisions with each other and with the walls of the container.

Kinetic theory of gases explains the macroscopic properties of gases, such as pressure, temperature, viscosity, thermal conductivity, and volume, by considering their molecular composition and motion. The theory posits that gas pressure results from particles' collisions with the walls of a container at different velocities.

Kinetic molecular theory defines temperature in its own way, in contrast with the thermodynamic definition.

Under an optical microscope, the molecules making up a liquid are too small to be visible. However, the jittery motion of pollen grains or dust particles in liquid are visible. Known as Brownian motion, the motion of the pollen or dust results from their collisions with the liquid's molecules.

The four laws of thermodynamics

The fundamental principles of thermodynamics were originally expressed in three laws. Later, it was determined that a more fundamental law had been neglected, apparently because it had seemed so obvious that it did not need to be stated explicitly. To form a complete set of rules, scientists decided this most fundamental law needed to be included. The problem, though, was that the first three laws had already been established and were well known by their assigned numbers. When faced with the prospect of renumbering the existing laws, which would cause considerable confusion, or placing the pre-eminent law at the end of the list, which would make no logical sense, a British physicist, Ralph H. Fowler, came up with an alternative that solved the dilemma: he called the new law the “Zeroth Law.” In brief, these laws are: 

The Zeroth Law states that if two bodies are in thermal equilibrium with some third body, then they are also in equilibrium with each other. This establishes temperature as a fundamental and measurable property of matter. 

The First Law states that the total increase in the energy of a system is equal to the increase in thermal energy plus the work done on the system. This states that heat is a form of energy and is therefore subject to the principle of conservation.

The Second Law states that heat energy cannot be transferred from a body at a lower temperature to a body at a higher temperature without the addition of energy. This is why it costs money to run an air conditioner.

The Third Law states that the entropy of a pure crystal at absolute zero is zero. As explained above, entropy is sometimes called "waste energy," i.e., energy that is unable to do work, and since there is no heat energy whatsoever at absolute zero, there can be no waste energy. Entropy is also a measure of the disorder in a system, and while a perfect crystal is by definition perfectly ordered, any positive value of temperature means there is motion within the crystal, which causes disorder. For these reasons, there can be no physical system with lower entropy, so entropy always has a positive value.

The science of thermodynamics has been developed over centuries, and its principles apply to nearly every device ever invented. Its importance in modern technology cannot be overstated

Additional guidelines for organizing a lesson 

Students can deduce topic of the lessen and objectives, for clarification you can show topic and the learning objectives on the presentation.

Then Subject-specific vocabulary & terminology will be presented to the students and their activities during the research work will be explained.

Then teacher will give the worksheet on the concepts studied previously. Students attempt the questions in groups as they engage in discussion. The teacher helps the learners with difficulties in answering the questions.

Reinforce the LO’s: answer any questions students may have/clarify understanding. Students reflect on their learning.  

At the end of the lesson teacher will give homework.

Additional multilevel (on differentiation) tasks

Each chapter has extra tasks which you would use for high level students.

Recommendations for formative assessment

1)      Use the answers provided to assess students’ understanding and the manner of application of the all terms concept knowledge

2)      Provide a general feedback for every given point (pay attention to give a fully explained feedback to the points that were not given)

3)      You can change the numbers in calculations according to the student’s ability

Answers, criteria for assignments, additional materials for the lesson

Answers:

Q1.

D

[1]

Q2.

(a)     kinetic energy of ball =  × mυ² =  × 0.060 × (50)² = 75 J (1)

(1)

(b)     kinetic energy of one atom  kT (1) ( × 1.38 × 10^–23 × T)

one gram contains  × N_A (= 1.5 × 10²³) atoms (1)

total internal energy = 1.5 × 10²³ ×  × 1.38 × 10^–23 × 48 = 150 J (1)

(3)

(c)     energy of helium gas at 48 K is twice that of tennis ball
∴energies equal when helium gas has a temperature of 24 K (1)

(1)

[5]

Q3.

(a)     (i)      more collisions (with wall) per second (1)
and more momentum change per collision (1)
greater force because more momentum change per second (greater pressure) (1)

(ii)     (same pressure) faster molecules so more momentum change per collision (1)
greater volume, fewer collisions per second [or greater volume
to maintain same pressure] (1)

max 4

(b)     (i)       (1) = 5.94 × 10^–3 m³ (1)

(ii)      (1)

= 1000 K (727 °C) (1)

4

[8]

Q4.

(a)     (i)      Clear statement that for isothermal pV =constant or p₁V₁ = p₂V₂ ✓
Applies this to any 2 points on the curve AB ✓
e.g. 1.0 × 10⁵ ×1.2 × 10⁻³ = 4.8 × 10⁵ × 0.25 × 10⁻³
120 = 120

Allow pV = c applied to intermediate points estimated from graph e.g. V = 0.39 × 10⁻³, p = 3 × 10⁵

2

(ii)     W = p Δv
= 4.8 × 10⁵ × (0.39 − 0.25) × 10⁻³
= 67 J ✓

1

(b)     

Any horiz line correct up to max 3
Give CE in B → C if ans to ii used for W
If no sign take as +ve

max 3

(c)     η_overall = 47 / 235 = 0.20 or 20% ✓

1

(d)     Isothermal process would require engine to run very slowly / be made of material of high heat conductivity ✓
Adiabatic process has to occur very rapidly / require perfectly insulating container / has no heat transfer ✓
Very difficult to meet both requirements in the same device ✓
Very difficult to arrange for heating to stop exactly in the right place (C) so that at end of expansion the curve meets the isothermal at A ✓

Do not credit bald statement to effect
adiabatic / isothermal process not possible - must give reason
Ignore mention of valves opening / closing, rounded corners, friction, induction / exhaust strokes

wtte

max 2

[9]

Q5:

Initial length of wire = L =  2 m, Diameter of wire = 2 mm, Radius of wire 2/2 = 1 mm = 1 × 10^-3 m, Weight attached = m = 2 kg, Increase in length = l = 0.24 mm = 0.24 × 10^-3 m, g = 9.8 m/s² . Stress = ?, Strain = ?, Young’s modulus of material = Y = ?

Stress = F / A  = mg /π r²

∴  Stress =  ( 8 × 9.8) /(3.142 ×(1 × 10^-3)²)

∴  Stress =  ( 8 × 9.8) /(3.142 ×  1 × 10^-6)

∴  Stress =  2.5× 10⁷ N/m²

Strain = l / L =   0.24 × 10^-3 / 2

Strain =0.12 × 10^-3 =1.2 × 10^-4

Now, Young’s modulus of elasticity= Y = Stress / Strain = ( 2.5× 10⁷) / (1.2 × 10^-4)

Y = 2.08 × 10¹¹ N/m²

Ans : Stress =  2.5× 10⁷ N/m², Strain  =1.2 × 10^-4 , Young’s modulus of elasticity= 2.08 × 10¹¹ N/m²

Q6:

Initial length of wire = L =  2 m, Cross-sectional area = A =  10^-4 m, Stretching weight = 102 kg wt = 102 × 9.8 N, Increase in length = l = 0.1 cm = 0.1 × 10^-2 m = 1 × 10^-3 m, g = 9.8 m/s² .

Stress = ?, Strain = ?, Young’s modulus of material = Y = ?

Stress = F / A  = mg /A

∴  Stress =  ( 102 × 9.8) /10^-4

∴  Stress =  1 × 10⁷ N/m²

Strain = l / L =   1 × 10^-3 / 2

Strain = 0.5 × 10^-3 = 5 × 10^-4

Now, Young’s modulus of elasticity= Y = Stress / Strain = ( 1 × 10⁷) / ( 5 × 10^-4)

Y = 2 × 10¹⁰ N/m²

Ans : Stress =  1 × 10⁷ N/m², Strain = 5 × 10^-4 , Young’s modulus of elasticity= Y = 2 × 10¹⁰ N/m²

Q7:

Initial length of wire = L = 3 m, radius of wire = 0.5 mm = 0.5 × 10^-3 m, = 5 × 10^-4 m,Force applied =49 N, Young’s modulus for steel = Y = 2.1 × 10¹¹ N/m².

Stress = ?, Strain = ?, elongation = ?

Stress = F / A  = mg /π r²

∴  Stress =  49 /(3.142 ×(5 × 10^-4)²)

∴  Stress = 49 /(3.142 × 25 × 10^-8)

∴  Stress = 6.238 × 10⁷ N/m²

Now, Y = Stress / Strain

∴  Strain = Stress / Y =  (6.238 × 10⁷ ) / (2.1 × 10¹¹)

Strain = 2.970 × 10^-4

Now, Strain = l / L

∴ l = Strain  × L

∴  l = 2.970 × 10^-4  × 3

∴  l = 8.91 × 10^-4  m = 0. 891 × 10^-3  m = 0.891 mm

Ans: Stress = 6.238 × 10⁷ N/m², Strain =  2.970 × 10^-4, Elongation = 0.891 mm.

Q8:

Initial length of wire = L =  1 m, Diameter of wire = 2 mm, Radius of wire = 2/2 = 1 mm = 1 × 10^-3 m, Load attached = m = 40 kg, Young’s modulus of material = Y = 7 × 10¹⁰ N/m².

Stress = ?, Strain = ?, Force constant = ?

Stress = F / A  = mg /π r²

∴  Stress =  ( 40 × 9.8) /(3.142 ×(1 × 10^-3)²)

∴  Stress =  ( 40 × 9.8) /(3.142 ×  1 × 10^-6)

∴  Stress =  1.25 × 10⁸    N/m²

Now, Y = Stress / Strain

∴   Strain = Stress / Y  =  1.25 × 10⁸  / 7 × 10¹⁰

∴   Strain = 1.78 × 10^-3

Now, Strain = l /L

∴ extension = l = Strain × L

∴  l = 1.78 × 10^-3 × 1

∴  l = 1.78 × 10^-3 m

Now, force constant K = F/l = mg/l = ( 40 × 9.8) /(1.78 × 10^-3)

Force constant K = 2.2 × 10⁵  N/m

Ans: Stress =  1.25 × 10⁸    N/m²,  Strain = 1.78 × 10^-3,  Force constant = 2.2 × 10⁵  N/m

Q9:

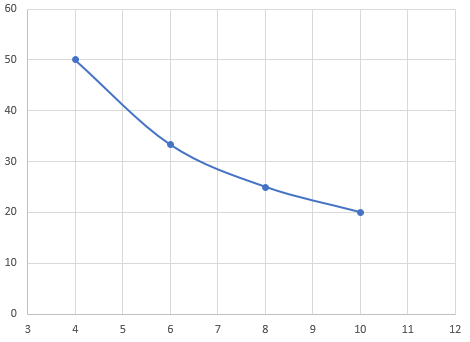
Isothermal process => T = const

P₁·V₁ = P₂·V₂

V₂ =  

V₂ =  

V₂ = 50 m³

The gas will expand, but the pressure will decrease

P(V) graph

V(T) graph

P(T) graph

List of useful links and literature

Скачано с www.znanio.ru