MAGNETIC FORCES

Example 3

AB and BC, joined at B. carrying a current of 2.0 A and subjected to a magnetic field of flux density 001 T direction in the plane ABC at to AB. Both AB and BC are 5_Ocm long. The angle ABC is 60'. Calculate the forces AB and BC What mmerncnt do tlx two forces together try to prcxlucc?

Method

The force on AB is

F o.(ns7 x 2.0 x S x 10-2

The force on BC is but. whic the force AB is upwards out Of the the left-hand rule gives thc force on BC to These forces therefore a couple the line BD in the diagram. and ngatim this c-sFcted.

8.7 x 10-4 N, Rotaú'n aNNt BD. Force on a charged particle moving through a magnetic field

Here q is the charge carried by the particle, v is the particle's vekxity and B is the magnetic flux density             to v.

Wc arc B to IXrrx•ndÉular to v. Otherwise B must be replaced in the formula by its perpendicular to v, since only this is effective. The direction Of F is Of given the left-hand rule (and that

this rule considers current direction, which for the movement Of particles such as electrons will be opposite to that of the particle velocity).

Example 4

An electron is moving with a speed of 10 ⁷ ms" ^I perpendicular to a magnetic field having a uniform flux density of oun2T.

(a) Calculate the force on the electron.

(b) Calculate the radius of the circular path followed by the ( Electron Ch e = I , 6 I C.

9.0 x IO-

Note: A •uniform' field is a constant field. i.e., it has the same B value for all pans of the electron•s path. Such fields can be obtained with magnets, coils or solenoids (see Chapter 25).

Method

(a) F Bqv or Be.' when e is used to dcnotc the inwards

= 7.0 x 10-2 m or 7.0cm

Answers

(a) N               (b) 7.Oan

Couple on a coil

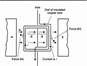
FO. 23.5 Couple on a coil

In Fig. 23.5 a force BIL acts on each vertical wire. If there are n turns of wire on the coil. the total force is BILn on each side Of the coil.

199 geschtit:tcs

"ONS FOR A-LEVfL PHYSICS

The torque due to this pair Of forces (a'uple) is C = 2BlLnR. However. the "'il area A equals 2RL, so that

(233)

If the magnetic field is radial (see Fig. 23.6a). then B is always parallel to the plane Of the even when the coil is allowed to rotate. and C — HAIn still. If instead the field is uniform (sce Fig. 23.6b and c). then the component of B which is effective is B cos o (sce diagram). and the torque

In an ordinary mosing-coil meter the current to be measured flows through the coil, the field is radial, and the torque BAIn turns the coil. The turning tightens a spring which therefore produces an torque of k newlon metre per unit angle Of rotation.

coil comes to restWhen BAIn = kO, where the angle of rotation of the coil O is in degrees or radians.

The torque BAIn is also used to prtxluce rotation in simple electric motors.

200

Example 5

A tnoving coil mctcr has a coil with 40 turns, cach with an area Of 20cm:. It is suspended in a vertical plane and its sides are perpendicular to a radial magnetic fieldof0-30T.

(a) Calculate the torque on the coil When a current Of flows through it.

(b) If the has a resistance of and a sensitivity Of fun What series resistance is necdcd to convert the rnetcr to a 10mVFSD meter?

Method

(a) Torque

The Earth's magnetism

In the United Kingdom the direction Of the magnetic flux density due to the Earth's magnetism makes an angle O (called the •angle Of dip') Of about 70' to the horizontal. The horizontal coml¾'nent of this flux density B is B cos o, and the vertical component is  = BsinO.

Note also that

Bo sin O

= BsinO) = cos = BC, tan O, where O is the angle of dip as shown in Fig. 23.7.

MAGNETIC FORCES An electron moving at a steady speed of 106 ms -I passes txtween two flat, parallcl metal plates 2.0can apart with a PD of

Exercise 23.1

(Where necessary take to tx4z x                H m-

Two very long parallel wires m apart in air each carry a alrrcnt Of 50 A. What the force. in newtons, each metre length of wire?

2  A horizmtal wire Of length 40cm is moving vertically dm•nwards, with a current of 1.0 A through it. If the plane in Which the Wire mmes is to a flux of O. I T, cakulate on the wire duc to the

3  A moving coil meter a 50-turn measuring I .0cm 20cm. It is in a radial magnetK• of flux density O. 15 T arui its a torsional anstant of 3.0 x 10 N m rad What current is required to gne a deflection Of

4  In Fig. 23.8 a flat, rectangular coil is fitted symmetrically on an axle and lies in a horizontal plane. Of 10 turns Of insulated Wire and its dimensions are as sh(Nn in the

        If a current of ZOA           round the coil

(a) What size is the vertical force on side BC caused by interaction txtween the current and the Earth's magnetic field? (Take the horizontal                                          of this field to

1.6 10-'T.)

(b) Cakulate total the due to this to the simuar forœ on skk DA.

(c) Cakulatc t•al that wtulld expcricnccd by con if its planc were at an ange of 20' to horizmtaL

between tiEm. The electron is kept traveling in a straight line perpendicular to the electric field between the plates by applying a magnetic field to the electron's path and to the electric late:

(a) the intensity Of the electric field (b) the magnetic flux density needed.

(Hint: the electron charge is not needed. It carxcls.)

Exercise 23.2:

Examination questions

Two long, straight, parallel wires in a vacuum are 025 m apart.

(i)  The Wires each carry a current Of 240 A in the Same direction. Calculate the force between the wires per metre of their length. Draw a sketch showing clearly the direction Of the force Ott each Wire.

(ii) The current in one of the wires is reduced to 064 A. Calculate the current needed in the second wire to maintain the same force

Wires per metre Of their length

(Take = 41 x 10-'Hm -l )

ICCEA 21"), partl

In Fig. 23.9, PORS is a rectangular coil consisting of N turns of wire and carrying current l. The plane of PORS is parallel to a uniform magnetic field of flux density B. The length of PO is L and the length Of

geschtit:tcs