Physics Grade 10 Gas laws Ideal gas law Worksheet

Worksheet

Cambridge 9702_s11_qp_42     Q2

1. (a) State what is meant by a mole.                                                                                                     [2]

 (b) Two containers A and B are joined by a tube of negligible volume, as illustrated in Fig. 2.1.

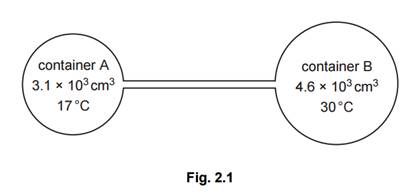
The containers are filled with an ideal gas at a pressure of 2.3 × 10⁵ Pa.

 The gas in container A has volume 3.1 × 10³ cm³ and is at a temperature of 17 °C.

 The gas in container B has volume 4.6 × 10³ cm³ and is at a temperature of 30 °C.

 Calculate the total amount of gas, in mol, in the containers.                                                                   [2]

Cambridge 9702_s12_qp_41         Q2

2. (a) The kinetic theory of gases is based on some simplifying assumptions.

 The molecules of the gas are assumed to behave as hard elastic identical spheres.

 State the assumption about ideal gas molecules based on

 (i) the nature of their movement,                                                                                                          [1]

 (ii) their volume.                                                                                                                                   [2]

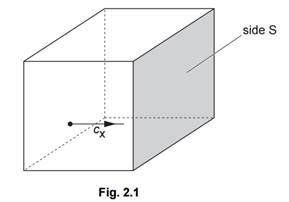(b) A cube of volume V contains N molecules of an ideal gas. Each molecule has a component c_X of velocity normal to one side S of the cube, as shown in Fig. 2.1.

The pressure p of the gas due to the component c_X of velocity is given by the expression

pV = Nmc_X²

where m is the mass of a molecule.

Explain how the expression leads to the relation

pV = 1/3 Nm<c²>

where <c²> is the mean square speed of the molecules.                                                                            [3]

(c) The molecules of an ideal gas have a root-mean-square (r.m.s.) speed of 520 m s^–1 at a temperature of 27 °C.

 Calculate the r.m.s. speed of the molecules at a temperature of 100 °C.                                                 [3]

Cambridge 9702_s04_qp_4              Q2

3. The pressure p of an ideal gas is given by the expression ,      

(a) Explain the meaning of the symbol <c²>.                                                                                        [2]

(b) The ideal gas has a density of 2.4 kg m^–3 at a pressure of 2.0 × 10⁵ Pa and a temperature of 300 K.

(i) Determine the root-mean-square (r.m.s.) speed of the gas atoms at 300 K.                                         [3]

(ii) Calculate the temperature of the gas for the atoms to have an r.m.s. speed that is twice that calculated in (i).

[3]