Тема урока:  Логарифмические неравенства.

Тип урока: Урок – закрепление с элементами нетрадиционного урока.

Цель урока:      1. Вспомнить определение логарифма; основные свойства.

                           2. Закрепить решение простейших логарифмических уравнений.

                           3. Научить мыслить творчески; решать самостоятельно.

Оборудование: 1. Раздаточные материалы.

                            2. Наглядное пособие (лабиринт).

                            3. Доска, мел.

План урока:       1. Подготовительный момент ( 2 мин.).

                            2. Закрепление пройденного с записями на доске ( 8 мин).

                            3. Самостоятельная работа ( 20 мин.) – игра «Лабиринт».

                            4. Подведение итогов (5 мин.), выставление оценок в журнал.

                            5. Домашнее задание с объяснением  ( 5 мин.).

Ход урока:       1этап.

На доске записана тема урока с датой. Преподаватель ставит цель урока и знакомит с кратким планом.

                Вопросы учащимся:

         1.Что называется логарифмом числа b  по основанию а.

 Определение: Логарифмом числа b по основанию а называется показатель степени, в которую нужно возвести основание а, чтобы получить число b,

т. е. - основное логарифмическое тождество.

Учащиеся комментируют примерами:

а)  т. к.  .       б)  т. к. .         в)  т. к. .

1.     Основные свойства логарифмов:

На одной половине доски – свойства, на другой примеры:

а) ;

б) ;

в) ;

г) ;

д) ;

е) ;

к) .

2.     Решите простейшие уравнения.

                   а)                                            б)                         

                            х=25.                                                      х=.

                       в)                                                г) 

                       .                                                х=100.

                                                д)  

                                                    3-х=1

                                                      х=2.

2 этап.      Игра «Лабиринт».

Перед каждым учащимся материалы с заданием.

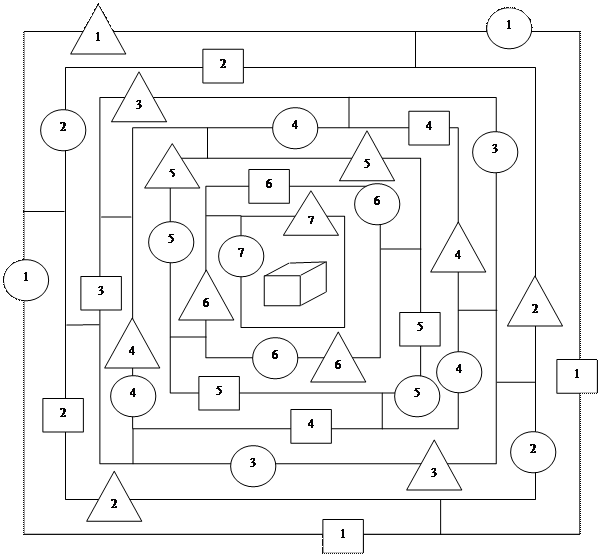
Познакомив учащихся с правилами игры, преподаватель советует перед началом работы просмотреть все 21 задание и выбрать оптимальный путь передвижения по лабиринту. (Учащиеся сталкиваются с проблемой выбора, но не все с ней могут успешно справиться).

Даже не достигнув конечной цели, можно получить хорошую оценку. Определяющую роль при ее выставлении играет не число сделанных заданий, а их сложность и качество работы.

Если задача не сделана или решена неверно, то баллы не начисляются.

Игрок, получивший оценку «3», несмотря на все старания, так и не дошел до сундука с сокровищами, очевидно, заблудившись в коридорах лабиринта.

Оценка «4» свидетельствует о том, что игрок успешно преодолел почти все преграды на своем пути и добрался до сундука.

Игрок, получивший оценку «5», оказался более удачливым. Но больше всего повезло тому, кто добравшись до сундука, унес его содержимое с собой. В результате награда – две высшие оценки.

3 этап.   Подведение итогов.

Учащиеся сами ставят себе оценки.

4 этап.     Домашнее задание.

На доске:        ( решаем введением новой переменной).

                                                                                                                  (отв. 100).

Это задание тем, кто получил «4» или «5» .

  Чтобы исправить неудовлетворительную оценку, задания

               1.  ;

                2. ;

Найдите х, если

                    3. 

                    4. 

                     5. 

Использована литература:

1.     Учебник «Алгебра и начала анализа» под редакцией А.Н. Колмогорова.

2.     Журнал «Математика в школе» №7, 2004г.

    3. Учебник «Алгебра и начала анализа» под редакцией Ш. А. Алимова.

Лабиринт

Стоимость задач

Критерии оценки

Карточка с заданиями.

1. ;

2. ;

3. ;

4. ;

5. ;

6. ;

7. .

1. ;

2. ;

3. ;

4. ;

5. ;

6. ;

7. .

1. ;

2. ;

3. ;

4. ;

5. ;

6. ;

7. .

Ответы к заданиям.

1.     .                                                1.      3.

          2.     0,09.                                             2.     .

          3.      4.                                                 3.     36

          4.      4.                                                 4.       3.

          5.    .                                                5.      2.

          6.      81.                                                6.     4,5.

          7.       2.                                                 7.      –1.

1.     2;  3.

2.     –10.

3.     5;  7.

4.     -5;  2.

5.      ;  16.

6.      0,0081;  .

7.      Æ.