План

 «Периодичность тригонометрических функций»

Цели урока:

ú  демонстрация возможностей работы с интерактивной доской;

ú  повторение свойств функций;

ú  знакомство с определением  периода   функции;

ú  рассмотрение правил нахождения периодов тригонометрических функций;

ú  рассмотрение заданий ЕГЭ по  нахождению периодов функций.

Требования к знаниям, умениям и навыкам учащихся

Учащиеся должны знать:

·         вид тригонометрических  функций и их свойства;

·         назначение программы «Графопостроитель» и способы  создания графиков функций в ней;

Учащиеся должны уметь:

·         строить графики тригонометрических функций;

·         строить графики функций в программе «Графопостроитель»;

Учащиеся должны иметь навыки:

• работы с компьютерами и периферийными устройствами;
• запуска программ в среде Windows;
• работы в программе «Графопостроитель»;
• работы с интерактивной доской.

Формы организации учебной деятельности:

• фронтальная работа с классом;
• индивидуальная тестовая работа за компьютером;
• групповая самостоятельная работа за компьютером;
• индивидуальная работа с использованием интерактивной доски.

Используемое программное обеспечение:

• Операционная система Windows;
• Программа «Графопостроитель»

План урока:

1.      Повторение свойств функций с использованием тренажера и интерактивной доски.

2.      Объяснение нового материала:

2.1.   определение периодической функции;

2.2.   доказательство периодичности тригонометрических функций;

2.3.   нахождение периодов функций, представляющих собой сумму непрерывных и периодических функций;

3.      Закрепление изученного материала:

3.1.   Решить №62,63,65.

3.2.   Построение графиков функций в программе «Графопостроитель».

3.3.   Объяснение заданий ЕГЭ.

4.      Групповая самостоятельная работа на компьютере с последующей проверкой.

5.      Подведение итогов урока и постановка задач для следующего урока.

Ход урока

1.     Повторение свойств функций

1.1.   Устно отвечаем на вопросы, используя тренажер: называем область определения функций , . Среди заданных функций находим четные, нечетные.

1.2.   На интерактивной доске по данному фрагменту достраиваем  графики четной или нечетной функции.

1.3.   На доске записана функция . Назвать ее свойство (нечетная).  Изменить ее запись с тем, чтобы она стала четной . Аналогично для функций ,  . Можно привести несколько вариантов ответа.

2.     Объяснение нового материала

2.1.   В природе и технике часто встречаются процессы, которые периодически повторяются  по истечении некоторого промежутка времени. Периодически  с периодом в 1 год меняется расстояние Земли от Солнца, с периодом в 1 лунный месяц меняются фазы луны и т.д.

Определение. Число Т, отличное от нуля, называется периодом функции  f, если для любого х, при котором эта функция определена, выполняются равенства

                        .

Периоды тригонометрических функций. (п.4.2) - прочитать и разобрать по учебнику.

Записать в тетрадях:

У периодической функции бесконечно много периодов: если Т – основной период, то и числа вида kТ  () также являются периодом.

Период функций  равен , период функций ,   равен .

2.2.   Доказать, что функция  имеет период .

Учащийся доказывает у доски

а) используя формулы приведения;

б) используя график функции.

Обобщая, формулируется правило построения периодической функции:

Для построения периодической функции с периодом  Т, нужно сначала построить часть графика на любом промежутке длины Т, а затем сдвинуть эту часть по оси х вправо и влево

на Т, 2Т, 3Т и т.д.

На интерактивной доске показывается построение периодической функции.

2.3.   Период функций, представляющих собой сумму непрерывных и периодических функций, равен наименьшему кратному периодов слагаемых, если он существует.

Наименьший положительный период для функций ,   равен , а для функций  ,  имеем .

Но, сумма двух периодических функций с одним и тем же периодом  Т, не обязательно имеет тот  же период: например:  и     имеют одинаковый положительный период, а их сумма не имеет наименьшего положительного периода.

3.     Закрепление  изученного материала.

3.1.   Решение у доски и в тетрадях:

№62. Докажите, что число Т является периодом функции f , если:

а) , .

Решение. Найдем период . Следовательно, период функции равен .

№64 (б, в). Найдите наименьший положительный период каждой из функций:

б) ;

в) .

Устно рассматриваем решение.

№65(а). Найдите наименьший положительный период  функции: .

Решение.  а) 

№65 (б, в). Устно.

б)  ;

в) .

3.2.   На ноутбуках с использованием программы «Графопостроитель» учащиеся строят графики тригонометрических функций:,  ,   и по графикам сравнивают периоды функций.

3.3.   Обзор заданий, составленных в виде тестов, которые могут быть предложены на ЕГЭ. Задания группы Б приготовлены на интерактивной доске таким образом, что сначала   появляется задание, а затем последовательно открывается решение задачи.

1. Периодическая функция  определена для всех действительных чисел. Ее период равен 10 и . Найдите значение выражения  .
2. Периодическая функция   с периодом, равным 10, определена на множестве  всех действительных чисел, причем на отрезке  она совпадает с функцией  . Найдите значение выражения  .
3. Изобразите график периодической функции с периодом равным 3. Составьте вопросы и ответьте на них (например, найти различные  значения  для выражений, которые придумывают учащиеся с учетом периодичности функции.)
4. Доказать, что функция  не является периодической. (Объясняет учитель с использованием интерактивной доски.)

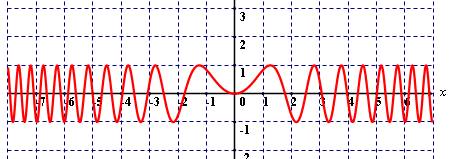
              Для доказательства непериодичности  какой-либо функции достаточно найти «неповторимую» точку графика, т.е. найти значение х такое, что точка графика с абсциссой х обладает свойством, которым не обладает никакая другая точка графика. Для данной функции таким значением является, например, . Действительно, из свойства четности функции следует, что  единственный корень уравнения  , при прохождении которого функция не меняет знак. Демонстрируется график функции на интерактивной доске.

Тест

1. Найдите наименьший положительный период функции

1) ;               2) ;             3) ;             4) .

2. Найдите наименьший положительный период функции

1)                2)              3)              4) .

3. Найдите наименьший положительный период функции  

1) ;              2) ;                        3) ;             4) .

4. Исследовать следующие функции на периодичность и найти наименьший положительный период, если он существует.

1. ;

1) не сущ.;                  2) 6;             3) ;               4) /3.

2) ;

1) не сущ.;                  2);                3) ;            4) .

с) ;

1) не сущ.;                  2) ;            3) ;             4) .

g) .

1) не сущ.;                  2) ;               3) ;            4) .

5.     Подведение итогов урока и постановка задач для следующего урока.

На уроке мы проделали следующую работу:

·         познакомились с новым свойством функции – периодичность,

·         изучили правила нахождения периодов  функций и применили их для решения задач,

·         учились строить графики функций, используя свойство периодичности,

·         провели самостоятельную работу по тесту, контролирующему знания по нахождению периодов функций.

Наиболее успешная работа отдельных учащихся на уроке была отмечена учителем.

Домашнее задание: п. 4.2, №№ 66, 67, 68(а, г), построить график функции  на промежутке .