Поделиться
.Уравнение, одна часть которого алгебраическая дробь, а другая – нуль урок.docx
Тема: Уравнение, одна часть которого алгебраическая дробь, а другая – нуль
Цель: способствовать развитию умений определять равносильность уравнений, проверять, является ли данное число корнем уравнения, определять верность высказывания, при каком значении переменной дробь равна нулю, при каком не существует.
Планируемые результаты:
Предметные:
Определяют при каком значении переменной дробь равна нулю, при каком не существует; решают уравнения.
Научатсярешать уравнения, где одна часть – алгебраическая дробь, а вторая равна нулю, по алгоритму; выделять основную информацию; решать уравнения, используя метод введения новой переменной; объяснять изученные положения на самостоятельно подобранных конкретных примерах.
Регулятивные: оценивать правильность выполнения действий на уровне адекватной ретроспективной оценки
Познавательные: ориентироваться на разнообразие способов решения задач
Коммуникативные: учитывать разные мнения и стремиться к координации различных позиций в сотрудничестве
1.Проблематизация, актуализация, мотивация.
Цель: обеспечение активной опоры на ранее усвоенные знания.
Добрый день, ребята! Послушайте о том, какой казус случился с молодым норвежским математиком Нильсом Абелем: связан он с потерей письма, написанного знаменитому французскому профессору математики из Сорбонны Огюстену Луи Коши в 19 веке. Перед вами его обрывок.
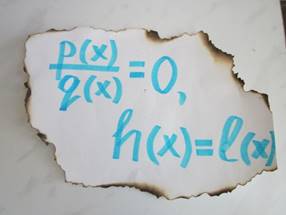
Рис.1
Что было написано в этом письме? Учащиеся: речь идёт о рациональном уравнении, записанном двумя способами, а значит и о решении рациональных уравнений.
Умеем ли мы решать рациональные уравнения, и если да, то какого уровня сложности?
Как вы считаете, чем мы займемся сегодня на уроке? Учащиеся формулируют тему урока. Ребята, великий, немецкий ученый А. Эйнштейн говорил о себе: «Мне приходится делить своё время между политикой и уравнениями. Однако уравнения, по-моему, гораздо важнее, потому что политика существует только до данного момента, а уравнения будут существовать вечно», скажите что должен уметь делать каждый из вас на сегодняшнем уроке? Учащиеся: уметь правильно и быстро решать дробно-рациональные уравнения.
Устно
1.Какое уравнение называется рациональным с неизвестным х?
Уравнение, левая и правая части которого есть рациональные выражения относительно х, называют рациональным уравнением с неизвестным х.
2.Что называется корнем уравнения с неизвестным х?
Корнем уравнения с неизвестным х называют число, при подстановке которого в уравнение вместо х получается верное числовое равенство.
3.Что значит решить уравнение?
Решить уравнение – значит найти все его корни или показать, что их нет.
4.Какие уравнения называют равносильными?
Уравнения, имеющие одинаковые корни, называют равносильными?
5.Как можно решить уравнение, одна часть которого нуль, а другая –
алгебраическая дробь?
Чтобы решить уравнение
= 0, где P(х)
и Q(х) – многочлены, надо найти корни уравнения Р(х) =
0 и подставить каждый из них в знаменатель Q(х) левой
части уравнения. Те из них, которые обращают знаменательQ(х)
в число, не равное нулю, являются корнями уравнения; других корней уравнение не
имеет.
Задания для устной работы
При каком значении х равна нулю дробь:
а)
: (0) б)
; (-3)в)
; (-2) г)
;(0) д)
; (7)ж)
(0)
2.Отработка и закрепление.
Цель: осуществление основных мыслительных операций; активное овладение новыми понятиями, операционными правилами, постоянная опора на личный опыт учащихся по введению новых понятий.
Каждый решает свой вариант, взаимопроверка, р/о. Общий итог.
1 вариант: №312(1ст)
2 вариант: №312(2ст)
3.Обобщение, систематизация, применение.
Цель: формирование аналитической способности выявления сходства и различия между алгоритмами решения уравнений; постоянная опора на личный опыт учащихся по введению новых понятий.
Решите уравнения и презентуйте свои решения другим: №313(1ст)
4.Обратная связь.
Цель: выявить уровень сформированной готовности к использованию вновь приобретённых знаний в единстве с ранее изученными правилами, к изучению следующей темы.
Решите уравнения:
1 вариант: 2 вариант:
=0
=0
=0
=0
=0 
=0
=0
=0
5.Повторение.
№879.
6.Подведение итогов урока. Рефлексия.
Вот и подошел к концу наш урок по решению рациональных уравнений, мне бы хотелось услышать, с чем вы сегодня уйдете с урока…
Продолжите любую из этих фраз на ваш выбор:
- Я познакомился с …
- Было не просто…
- У меня получилось…
- Хотелось бы…
- Мне запомнилось…
- Я попробую….
Оцените свою работу на уроке.
Д/з.
П 5.4; №№307; 313(2ст).
Решите уравнения:
1 вариант: 2 вариант:
=0
=0
=0
=0
=0
=0
=0
=0
Решите уравнения:
1 вариант: 2 вариант:
=0
=0
=0
=0
=0
=0
=0
=0
Решите уравнения:
1 вариант: 2 вариант:
=0
=0
=0 
=0
=0
=0
=0
=0
Решите уравнения:
1 вариант: 2 вариант:
=0
=0
=0
=0
=0
=0
=0
=0
Решите уравнения:
1 вариант: 2 вариант:
=0
=0
=0 
=0
=0
=0
=0
=0
Решите уравнения:
1 вариант: 2 вариант:
=0
=0
=0 
=0
=0
=0
=0
=0
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.
