План-конспект урока геометрии в 7 классе "Простейшие геометрические объекты"

Цель урока: познакомить учащихся с тем, что изучает геометрия, какой раздел геометрии называется планиметрией, какие фигуры в планиметрии называются основными; рассмотреть элементарные фигуры: точка, прямая, плоскость.

Задачи урока: сформировать умения оперировать понятиями: фигура, точка, прямая, плоскость. Решать задачи с применением простейших свойств фигур, задачи на нахождение геометрических величин.

Тип урока: освоение новых знаний.

Ход урока.

I.       Организационный момент. Мотивация к учебной деятельности.

Чтобы жить в гармонии с природой, нужно понимать языки, с которых мы могли бы общаться с ней. Галилео Галилей говорил: «Природа говорит языком математики: буквы этого языка - круги, треугольники и иные математические формулы, фигуры». И это поистине так. Куда бы мы ни обратили свой взор - вокруг геометрия. Какие геометрические фигуры мы встречаем в жизни?

II.    Вхождение в тему урока и создание условий для осознанного восприятия нового материала.

Геометрия – одна из наиболее древних наук. В переводе с греческого слово «геометрия» означает «землемерие» («гео» – по-гречески земля, а «метрео» – мерить).

Геометрии делится на планиметрию и стереометрию. Такие фигуры, как отрезок, луч, прямая, угол, окружность, круг, треугольник, прямоугольник, являются плоскими, то есть целиком укладываются на плоскости. Раздел геометрии, изучающий свойства фигур на плоскости, называется планиметрией (от латинского слова «планум» – плоскость и греческого «метрео» – измеряю).

В стереометрии изучаются свойства фигур в пространстве, таких как параллелепипед, шар, цилиндр, пирамида (показать модели). Мы начнем изучение геометрии с планиметрии

Планиметрия изучает свойства фигур на плоскости. Фигуры эти могут быть сложные и простые, а могут быть настолько простые, что их уже невозможно определить через другие фигуры. Такие фигуры называют элементарными. С их помощью описывают все многообразие мира геометрии. Что такое точка? Что такое прямая? Что такое плоскость?

III.   Изучение нового материала.

Один ученик работает около доски, остальные – в тетрадях.

1.      Начертите прямую (рис. 1.1). Как ее можно обозначить? (Прямая AB или а)

2.      Отметьте точку С, не лежащую на данной прямой, и точки D, E, K, лежащие на этой прямой (рис. 1.2)

В математике существуют специальные символы, позволяющие кратко записать какие-либо утверждения. Символы  и  означают соответственно «принадлежит» и «не принадлежит» и называются символами принадлежности.

3.    Используя символы принадлежности, запишите предложение «Точка D принадлежит прямой АВ, а точка С не принадлежит прямой а». (D АВ, Са)

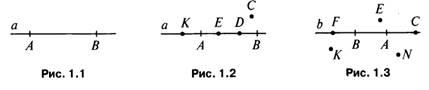
4.    Используя рис. 1.3 и символы запишите, какие точки принадлежат прямой b, а какие – нет. (F, B, A, Cb; K, E, Nb)

-       Сколько прямых можно провести через заданную точку А? (через заданную точку А можно провести множество прямых)

-       Сколько прямых можно провести через две данные точки? (только одну прямую)

-       Через любые две точки можно провести прямую? (Да)

Свойство прямой: Через любые две точки можно провести прямую, и притом только одну.

5.      Начертите прямые XY и MK, пересекающие в точке О (рис. 1.4)

Для того чтобы кратко записать, что прямые XY и MK пересекаются в точке О, используют специальный символ  и записывают так: XYMK=O.

- Сколько общих точек может быть у двух прямых? (Две прямые либо имеют только одну общую точку, либо не имеют общих точек)

6. На прямой а отметьте последовательно точки A, B, C, D. Запишите все получившиеся отрезки. (Получившиеся отрезки: AB, BC, CD, AC, AD, BD (рис. 1.5))

7. Начертите прямые a и b, пересекающиеся в точке М. На прямой а отметьте точку N, отличную от точки M.

а) Являются ли прямые MN и а различными прямыми?

б) Может ли прямая b проходить через точку N?

Решение:

а) Прямая MN и прямая а совпадают, то есть это одна и та же прямая (рис. 1.6)

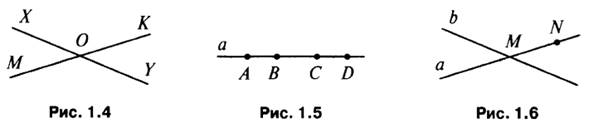
б) Прямая b не может проходить через точку N, так как она уже проходит через точку М, а через точки M и N можно провести прямую, и притом только одну (это прямая а).

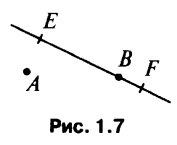
8. Дана прямая EF, AEF, B EF. Может ли прямая AB не пересекать отрезок EF? (Не может (рис. 1.7))

IV.   Применение изученного материала.

1.    Решите задачи №2, 5 (учебник)

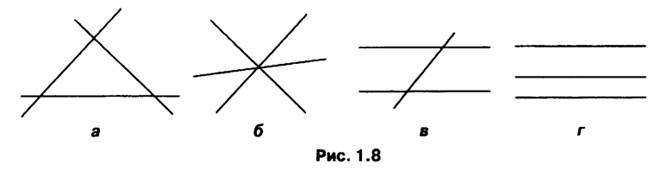
2.    Сколько точек пересечения могут иметь три прямые? Рассмотрите все возможные случаи и сделать соответствующие рисунки. (Ответ: рис. 1.8 а) три точки пересечения; б) 1 точка пересечения; в)2 точки пересечения; г) ни одной точки пересечения)

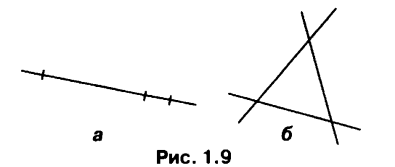
3.    На плоскости даны три точки. Сколько прямых можно провести через эти точки так, чтобы на каждой прямой лежали хотя бы две из данных точек? Рассмотрите все возможные случаи и сделать соответствующие рисунки. (Ответ: рис. 1.9 а) 1 прямая; б) 3 прямых)

V.                Рефлексия. Итог урока:

1.    Как называется наука, изучающая геометрические фигуры?

2.    Как называется часть геометрии, изучающая фигуры на плоскости (в пространстве)?

3.    Что означают символы , , ?

4.    Сколько прямых можно провести через две точки?

5.    Сколько общих точек могут иметь две прямые?

VI.             Домашнее задание: §1 – прочитать, выучить свойства, вопросы 1-3 стр. 26, №1, №4