План урока

План урока

1.Класс: 8                

2.Тема:Центр масс в треугольнике                      

3.Тип урока: Урок освоения новых знаний и умений

4.Цель урока: рассмотреть теорему о пересечении медиан треугольника

5.Планируемые результаты:

Личностные: овладение основными навыками исследовательской деятельности, установка на осмысление опыта, наблюдений, поступков и стремление совершенствовать пути достижения индивидуального и коллективного благополучия.

Предметные: решать задачи на нахождение длин, углов, площадей фигур.

6.Ключевые слова: теорема Фалеса.

7.На уроке предусмотрено использование следующих видов деятельности:«Галерея изображений (группа изображений по одной тематике)», «Самостоятельная работа».

Блочно-модульное описание урока

Этап 1/БЛОК 1. Освоение нового материала

1. Осуществление учебных действий по освоению нового материала.

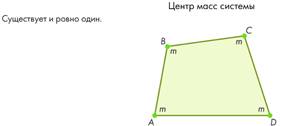
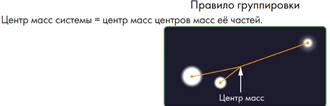
1) Обратите внимание, что мы сами выбираем, какие массы располагать в точках и в каких точках. Как выбрать массы - дело интуиции. Также, отметьте, что из задачи следует теорема Вариньона. Действительно, средние линии - диагонали, пересекающиеся и делящиеся пополам.

2) Дайте определение центроида - точка пересечения медиан, он же центр масс треугольника. Еще раз обратите внимание, что центром масс он будет только при равных массах в вершинах.

3) Пример задачи, когда имеет смысл расставлять не одинаковые массы, а хитро, чтобы центр масс попал в нужную нам точку.

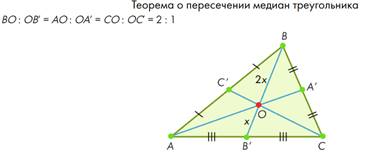
Теорема.Медианы треугольника пересекаются в одной точке, которая делит каждую медиану в отношении 2:1, считая от вершины.

Этап 2 /БЛОК 2. Применение изученного материала

1. Применение знаний, в том числе в новых ситуациях.

1) Одно отношение можно разобрать сразу. Остальные оставить на самостоятельный поиск

2) Вторая задача как раз про различные массы. Обратите внимание, что задача очень похожа на предыдущую, но центр масс «съехал» в сторону точки B. Значит, B тяжелее остальных точек. После обсуждения задачи, отметьте, что все 4 отрезка внутри четырёхугольника делятся точками пересечения на три равные части.

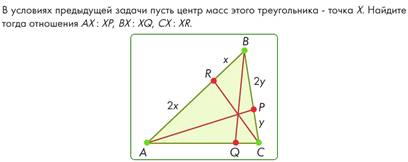
3) Третья задача уже не столько на геометрию масс, сколько о свойствах непосредственно центра масс треугольника.