План урока 8

Тема: « Квадратное уравнение и его виды»

Цель:

Закрепление:

 понятия   «Квадратное уравнение» и его виды;

умения решать квадратные уравнения.

Задачи:    

     Образовательная –  организовать самостоятельную деятельность учащихся по закреплению изученного материала;

      Развивающие – развивать умение выделять главное, обобщать изученные факты, умение логически излагать мысли;

       Воспитательные – способствовать формированию учебных и трудовых навыков, воспитанию аккуратности, внимательности, воли и настойчивости для достижения результатов.

Ход урока

I.    Вводно-мотивационный

Добрый день, ребята!

Решите анаграммы. ( в словах изменен порядок букв)

- ерокнь (корень)

- ниваренуе (уравнение)

- фекоцинетиф (коэффициент)

- таиимдкисрин (дискриминант)

Какая тема обьединяет написанные слова? (квадратные уравнения)

Значит что сегодня будем делать на уроке?

II. Работа по опорному конспекту: (на партах)

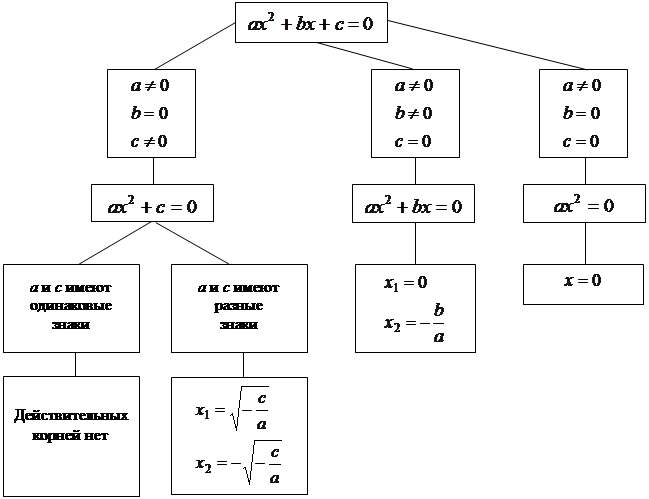
1)    Какое уравнение называется квадратным ?

Является ли квадратным уравнение:

48х²-х³-9=0  

3х-27=0           

 х²- 0,6х+5=0

3х²+12х=0             

5х²-27+2х =0 ?

2)      Какое уравнение называется полным квадратным ?

 Назовите коэффициенты a, b, c:

-2х²+3х+5=0,  

х²- 6х+15=0

Если квадратноек уравнение является полным, то какие способы решений существуют? (через дискриминант и по т.Виета)

Проверка дз №276.

Как по другому можно назвать эти уравнения? (приведенные)

Определение приведенного квадратного уравнения.

3)    Какое уравнение называется неполным квадратным ?

Решить устно.

2х²-7х=0                         1. х(2х-7)=0    х=0 или 2х-7=0

5х²=0                              2. х²=0:5      х=0            

х²-16=0                          3. х²=16       

III. Решив уравнение, ученик получит координаты точки, по которым необходимо будет в конце самостоятельной работы построить фигуру по ее координатам.( на ватмане заранее нужно построить координатную плоскость)

Координаты точек записывать по правилу: х₁  х₂.

«Настольная лампа»

1) х²+15х+44=0 (х₂;х₁)

2) х²+9х+8=0 (х₂;х₁)

3) х²+х=0 (х_1;х₂)

4) х²+6х=0 (х_1;х₂)

5) х²-4х-21=0 (х_1;х₂)

6) х²-10х+21=0 (х_1;х₂)

7) х²-6х=0 (х₂;х₁)

8) х²-х=0 (х₂;х₁)

9) х²+7х-8=0 (х₂;х₁)

10) х²+7х-44=0 (х₂;х₁)

Ответы к уравнениям на слайде.

Проверяем.

1)(-4;-11)

2)(-1;-8)

3)(-1;0)

4)(-6;0)

5)(-3;7)

6)(3;7)

7)(6;0)

8)(1;0)

9)(1;-8)

10)(4;-11)

Домашнее задание:

решение разноуровневых заданий

                 Учись, как решать:    

1.   2х²-7х=0                         1. х(2х-7)=0    х=0 или 2х-7=0

2.   5х²=0                              2. х²=0:5      х=0            

3.   х²-16=0                          3. х²=16       

Уровень  А

Решите уравнения:

5.Укажите  в квадратном уравнении его коэффициенты:  4х²+ 5х-17=0 (1б)

Уровень В

Решите уравнения:

Учись, как решать:

Подсказки №1

1) перенеси справа в левую часть, правую приравняй 0;

2) приведи подобные слагаемые;

3) реши неполное квадратное уравнение.

Подсказки №2

1) примени в правой части формулу разности квадратов;

2) перенеси справа в левую часть, правую приравняй 0;

3) приведи подобные слагаемые;

Уровень  С

Решите уравнение графически:

IV.     Рефлексия

Урок я хочу закончить   притчей.

Однажды молодой человек пришёл к  мудрецу и пожаловался ему: «Каждый день оп 5 раз я произношу фразу «я принимаю радость в мою жизнь, но радости в моей жизни нет». Мудрец положил перед собой ложку, свечу и кружку и попросил: «Назови, что ты выбираешь из них» «Ложку» , - ответил юноша.  «Произнеси это слово 5 раз», - сказал мудрец. «Я выбираю ложку», - послушно произнёс юноша 5 раз. «Вот видишь, сказал мудрец, - повторяй хоть миллион раз в день, ложка не станет твоей. Надо протянуть руку и взять ложку».

Дополнительный материал:

Продвинутые способы решения квадратных уравнений:

• Способ переброски
• По свойству коэффициентов
• С помощью циркуля и линейки
• С помощью номограммы
• Геометрический

Решение квадратных уравнений по свойству коэффициентов

Пусть дано квадратное уравнение ах² + bх + с = 0, где, а ≠ 0.

Свойство 1

Если, а + b + с = 0 (т.е. сумма коэффициентов уравнения равна нулю), то х₁ = 1, х₂ = с/а

Свойство 2

Если а – b + с = 0, или b = а + с, то х₁ = – 1, х₂ = – с/а

Пример:

2x² - 5x + 3 = 0 br>
3x² + 4x +1 = 0

Решите самостоятельно:

- чему равна сумма корней в каждом уравнении?

- общий корень всех этих уравнений?

- как вычислить второй корень?

Открыть на доске еще одно свойство квадратных уравнений:

Если в квадратном уравнении а+в+с=0, то х₁=1, х₂=с/а.

Задание учащимся  - придумать и решить квадратное уравнение с использованием этого свойства.

Проверка в группе.