
Тема урока: Теорема Виета и теорема, обратная ей
Тип урока: урок решения задач.
Учебная задача урока: Закрепить навыки в решении задач разных видов с помощью теоремы Виета и теоремы, обратной ей.
В результате урока ученик:
1) знает:
- определение приведенного квадратного уравнения;
- формулировку теоремы Виета и теоремы, обратной ей;
- виды задач, решаемых на основе теоремы Виета и теоремы, обратной ей.
2) умеет:
- сводить квадратное уравнение к приведенному квадратному уравнению;
- находить корни приведенного квадратного уравнения с помощью теоремы Виета;
- умеет по корням составлять квадратное уравнение.
Понимает:
- для чего применяется теорема Виета и теорема, обратная ей;
- как пользоваться теоремой Виета и теоремой, обратной ей, в решении более сложных задач;
Учебные
действия, формируемые на уроке:
• Личностные: умение учащегося
устанавливать связи между целью учебной деятельности и её мотивом, т.е. между
результатом учения, и тем, что побуждает деятельность, ради чего она
осуществляется, таким образом должна осуществляться осмысленная организация
собственной деятельности ученика
• Регулятивные: целеполагание как постановка учебной задачи на основе
соотнесения того, что уже известно и усвоено учащимся, и того, что ещё
неизвестно, планирование - определение последовательности промежуточных целей с
учётом конечного результата, оценка - выделение и осознание учащимся того, что
уже усвоено и что ещё подлежит усвоению, осознание качества и уровня
усвоения
• Коммуникативные: планирование учебного сотрудничества с учителем и
сверстниками, т. е. определение цели сотрудничества, функций участников,
способов взаимодействия, умение с достаточно полнотой и точностью выражать свои
мысли в соответствии с задачами и условиями коммуникации, владение
монологической и диалогической формами речи в соответствии с грамматическими и синтаксическими
нормами родного языка, умение доказывать собственное мнение
• Познавательные: анализ объектов с целью выделения признаков
(существенных, несущественных); выдвижение гипотез и их обоснование; построение
логической цепи рассуждений, доказательство; подведение под понятие; выведение
следствий; установление причинно-следственных связей.
Методы обучения: эвристическая беседа, репродуктивный, частично-поисковые, УДЕ.
Форма работы: фронтальная,
групповая.
Средства
обучения: традиционные,
презентация.
Структура урока:
I. Мотивационно-ориентировочная часть (10мин.)
II. Операционно-познавательная часть (32 мин.)
III. Рефлексивно-оценочная часть (3 мин.)
Структура урока
I. Мотивационно – ориентировочная часть.
1. Актуализация знаний.
- Какие из следующих уравнений являются приведенным квадратным уравнением:
![]() ;
;
![]() ;
;
![]() ?
?
( а) и в), т.к.
коэффициент перед ![]() равен 1)
равен 1)
- Какое уравнение называется приведённым?
(квадратное
уравнение, с коэффициентом 1 при ![]() , называется приведённым
квадратным уравнением)
, называется приведённым
квадратным уравнением)
- Устно найдите корни указанных приведённых квадратных уравнений. ( a) ![]() ; в)
; в) ![]() )
)
- Какой теоремой пользовались? (теоремой Виета)
- Сформулируйте теорему Виета. (если приведённое квадратное уравнение вида ![]() имеет неотрицательный дискриминант, то
сумма корней этого уравнения равна коэффициенту при
имеет неотрицательный дискриминант, то
сумма корней этого уравнения равна коэффициенту при ![]() , взятому с
противоположным знаком, а произведение корней равно свободному члену)
, взятому с
противоположным знаком, а произведение корней равно свободному члену)
- Корнями какого приведённого уравнения являются корни 6 и -11?
(![]()
- Какой теоремой пользовались? (теоремой, обратной теореме Виета)
- Сформулируйте теорему, обратную теореме Виета.
(если для чисел ![]() справедливы формулы
справедливы формулы
![]() , то
, то ![]() являются корнями уравнения
являются корнями уравнения ![]() )
)
2. Мотивация. Постановка учебной задачи.
Итак, на основе теоремы Виета и ей обратной теоремы можно решать ряд задач. Сегодня на уроке мы рассмотрим какие задачи и как решаются на основе указанных теорем.
II. Операционно – познавательная часть.
Записываем тему урока «Решение задач на теорему Виета и теорему, обратную ей».
№ 1:

- Какая теорема нам поможет составить уравнение? (теорема, обратная теореме Виета)
Решение:
![]()
![]()
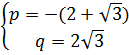
![]()
№ 2.
Сократите дробь:
![]()
- Что сначала нужно сделать, чтобы дробь с квадратными трёхчленами в числителе и знаменателе привести к виду, в котором её можно сокращать? (разложить числитель и знаменатель на множители, найдя корни квадратных трёхчленов)
- Предварительно можно что-то сделать, чтобы упростить дальнейшие вычисления? (да, вынести знак «-» из знаменателя перед дробью)
![]()
- А как нам разложить числитель и знаменатель на множители? (приравнять многочлены, которые записаны в них, к нулю и найти корни составленных уравнений)
- А какая теорема нам поможет найти корни? (Теорема Виета)
![]()
![]()
![]()
![]()
![]()
![]()
- Итак, мы нашли корни. Как мы теперь разложим числитель и знаменатель?
![]()
![]()
- Какая дробь получится?
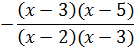
- Теперь мы можем её сократить? (Да)
- Что можно сократить? ( x-3¹0)
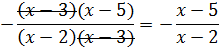
№ 3.
Не
вычисляя корней ![]() и
и ![]() квадратного уравнения
квадратного уравнения
![]() , найти:
, найти:
![]()
Решение:
- Прочитай условие.
- Выпиши данное квадратное уравнение.
![]()
- Какая формула записана в задании? (сумма сумма квадратов)
- Запиши формулу суммы квадратов для данного выражения.
![]()
- С чем схожи слагаемые в данной формуле? (с формулами теоремы Виета)
- Как нам применить теорему Виета к данному заданию? (записать формулы теоремы Виета для данного уравнения)
- Приведённое ли это уравнение? (да)
- Какие формулы получатся?
![]()
- Как нам теперь применить их к решению задания? (нужно подставить значения этих выражений в формулу суммы квадратов)
![]()
Задания для самостоятельной работы :
№ 1.

№
2. Не вычисляя корней ![]() и
и ![]() квадратного уравнения
квадратного уравнения
![]() , найти:
, найти:
![]()
№3.
Сократите дробь:
![]()
Ученики решают самостоятельно задания на листочках. После чего один из учеников собирает все работы и раздаёт в обратном порядке так, чтобы у каждого на руках была работа другого ученика. После проверяют по презентации правильность, исправляют ошибки в работе одноклассников.
Проверка:
№ 1.
Решение:
-
Пусть ![]() это корни исходного уравнения. А
это корни исходного уравнения. А ![]() – это корни искомого уравнения. В каком
отношении они находятся? Запиши в виде формул.
– это корни искомого уравнения. В каком
отношении они находятся? Запиши в виде формул.
![]()
- Сведём исходное уравнение к приведенному, разделив на 2 обе части уравнения.
![]()
- Тогда по теореме Виета
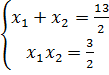
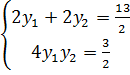
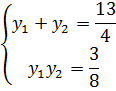
Тогда по теореме, обратной теореме Виета, искомое уравнение имеет вид:
![]()
![]()
№ 2.
Решение:
![]()
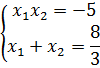
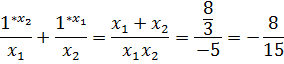
![]()
№3.
Решение:
![]()
![]()
![]()
![]()
![]()
После проверки друг друга ученики ставят оценку однокласснику, исходя из количества правильно решённых заданий:
3 правильно решённых задания - оценка «5»
2 правильно решённых задания - оценка «4»
1 правильно решённое задание - оценка «3»
Потом все листочки сдаются учителю и он ставит оценки согласно оценкам, выставленным самими учениками, предварительно проверив их объективность.
III. Рефлексивно-оценочная часть.
- Какова была цель урока? (закрепить навыки в решении задач разных видов с помощью теоремы Виета и теоремы, обратной ей.
-Достигли мы её? (да)
- Как мы её достигли? (решали задачи разных видов с помощью теоремы Виета и теоремы, обратной ей, работали в группах и у доски)
Домашнее задание:
№ 1: Составьте уравнение по его корням:
![]()
![]()
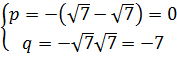
![]()
№
2:
Не вычисляя корней ![]() и
и ![]() квадратного уравнения
квадратного уравнения
![]() , найти:
, найти:
![]()
- Какая формула записана в задании? (сумма кубов)
- Запиши формулу суммы кубов для данного выражения.
![]()
- С чем схожи слагаемые в данной формуле? (с формулами теоремы Виета)
- Как нам применить теорему Виета к данному заданию? (записать формулы теоремы Виета для данного уравнения)
- Приведённое ли это уравнение? (нет)
- Что нужно сделать, чтобы оно стало приведённым? (поделить обе части уравнения на 3)
![]()
- Мы получили приведённое уравнение. Какие формулы получатся?
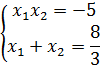
- Как нам теперь применить их к решению задания? (нужно подставить значения этих выражений в формулу суммы кубов)
![]()
- С
какой проблемой мы столкнулись? (мы не знаем значения выражения ![]() )
)
- Что это за формула? Как её можно расписать?
![]()
- Подставим это в наше выражение.
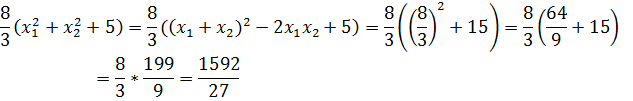
![]()
№3.
Сократите дробь:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
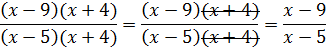
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.