План урока 9

Тема урока «Определение синуса, косинуса, тангенса, котангенса»

Вид урока  – урок – семинар

Тип урока – урок изучения нового материала

Время проведения  – 40 минут

Цели урока – организация продуктивной деятельности обучающихся, направленной на достижение ими следующих результатов:

·         Предметных:

– систематизация уже имеющихся знаний по тригонометрии;

– введение новых определений синуса, косинуса, тангенса, котангенса  углов;

– сформировать умения и навыки нахождения значений выражений,     содержащих синусы, косинусы, тангенсы, котангенсы углов;

–умение анализировать материал, использовать имеющиеся знания и опыт; выявлять аналогии, делать выводы;

–закрепление навыков использования определений и таблицы значений при решении задач.

·          Метапредметных:

 познавательная деятельность:

–изложение информации, интерпретируя факты, разъясняя значение и смысл теории;

–выдвижение предположений, понимание необходимости их проверки на практике;

–применение новых знаний для решения проблемных задач, умение устанавливать причинно следственные связи;

 информационно – коммуникативная деятельность:

– умение участвовать в диалоге, признавать право на иное мнение;

–умение точно, грамотно излагать свои мысли, выстраивать аргументацию;

– умение предвидеть возможные последствия своих действий;

регулятивная деятельность:

– овладение навыками самоконтроля и оценки своей деятельности;

–совершенствование умения совместной деятельности с другими ее участниками.

·         Личностных:

 –  умение ставить перед собой цель, планировать деятельность;

  – умение точно и грамотно излагать свои мысли;

  – умение контролировать процесс и результат учебной  деятельности;

  –освоение приёмов самостоятельного открытия  знаний и выполнения заданий;

   – приобретение опыта  по принятию ответственности за свои решения.

Формы организации учебной деятельности – индивидуальная, групповая

Методы  обучения – частично-поисковый, метод стимулирования учебно-познавательной деятельности.

Применяемые технологии: 

·       технология  критического мышления

·       ИКТ

Требования к результатам усвоения учебного материала:

обучающиеся должны знать:

·       определения синуса, косинуса, тангенса и котангенса угла;

·       таблицу значений синусов, косинусов, тангенсов, котангенсов углов;

обучающиеся должны уметь:

·       пользоваться таблицей значений;

·       находить значения выражений, содержащих синусы, косинусы, тангенсы, котангенсы углов.

Оборудование: компьютер, проектор, экран, доска, мел, презентация, раздаточный материал

Структура урока:

1.       Стадия «Вызова»

–  Организационный момент. 2 мин.

–  Актуализация знаний учащихся. 5 мин.

2.       Стадия «Осмысления»

–  Изучение нового материала. 12 мин.

3.       Стадия «Рефлексия»

– Релаксация, историческая справка. 3 мин.

– Закрепление нового материала. 12 мин.

– Подведение итогов урока. 3 мин.

– Домашнее задание. 2 мин.

                                       Ход урока.

1. Стадия «Вызова»

–  Организационный момент

Приветствие, проверка явки, заполнение журнала.

–  Актуализация знаний учащихся

Учитель:  Мы живём в реальном мире, и для его познания нам необходимы знания. Сегодня мы продвинемся еще дальше на пути нашего познания и рассмотрим понятия синуса, косинуса, тангенса и котангенса углов. Запишем тему  урока. Но сначала давайте вспомним, что же мы уже умеем.

Прием «Мозговой штурм»

Учитель: 

Переведите градусы в радианы

Переведите радианы в градусы

Определите четверть, в которой лежит угол

      За каждый правильно выполненный пункт на полях ставим 1 балл.

     Сегодня на уроке Вы сами будете оценивать результаты своей работы. За каждый правильный ответ или за выход к доске на полях тетрадки ставьте 1балл, в конце урока посчитаете количество баллов и поставите сами себе отметку, оценив свою деятельность на уроке.

2. Стадия «Осмысления»

     В ходе беседы с учащимися учитель вводит понятия синуса, косинуса, тангенса и котангенса угла.

Учитель:

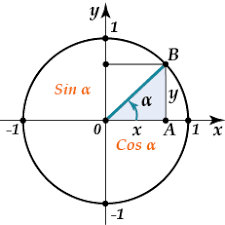
     Начертите декартову систему координат и единичную окружность с  центром в начале координат. Поставьте  в первой четверти на окружности произвольную точку  - В(х;у). Дугой выделите угол , соответствующий точке В (откладывается от положительной полуоси Ох).

     Значит, положение точки В  можно задать двумя способами: с одной стороны, координатами (х; у), а с другой стороны, с помощью угла поворота этой точки вокруг начала координат. Т.о., если  положение точки  можно задать двумя способами, значит, между ними должна быть  связь, т.е., можно ввести тригонометрические функции, которые свяжут координаты точки и соответствующий ей угол.

Учитель: 

     Из точки В(х;у) опустим два перпендикуляра на оси ОХ и ОУ и рассмотрим треугольник ВОА. Вспомним, что такое синус и косинус острого угла в прямоугольном треугольнике?

Ответы обучающихся.

Определение: 

Синусом угла  называется ордината точки В

Как видно из рисунка, значения синуса лежат между -1 и 1. Теперь ось ординат будем называть осью синусов.

Определение: 

    Косинусом угла называется абсцисса точки В.

Как видно из рисунка, значения косинуса лежат между -1 и 1. Теперь ось абсцисс будем называть осью косинусов.

Определение: 

Тангенсом угла называется отношение синуса угла к его косинусу.

Определение:

    Котангенсом угла называется отношение косинуса угла к его синусу.

Оси тангенсов и котангенсов нам пока не нужны, мы введем их при решении уравнений.    

Важно помнить!

     Синус и косинус определены  для любых углов α.

     Тангенс определен для всех углов, кроме тех, в которых   

     Котангенс определен для всех углов, кроме тех, в которых   

     Запишите таблицу основных значений синуса, косинуса, тангенса и котангенса. (Слайд 10)

Таблица значений тригонометрических функций

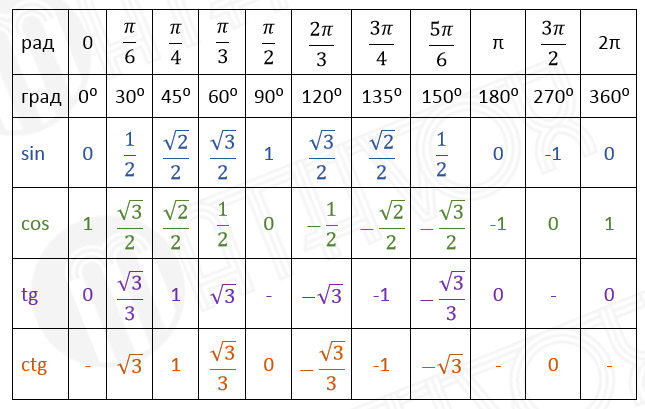
     Чтобы найти значение одной из функций от какого-нибудь угла, например , значение ищем на пересечении соответствующей строки, в нашем  случае третьей, и соответствующего столбца, в нашем случае – 7-го, т.е.

.

3. Стадия «Рефлексия»

– Релаксация

1)Упражнение для улучшения мозгового кровообращения:

Сидя, вытяните и положите на парту руки. Поверните голову направо, затем налево, затем плавно наклоните голову назад, потом вперёд. Медленно повторите 2 – 3  раза.

2) Гимнастика для глаз.

Быстро поморгайте. Закройте глаза и спокойно посидите, медленно считая до 5. Повторить 2 – 3 раза.

 – Историческая справка 

     Древнегреческие ученые владели методами решения прямоугольных треугольников. Астрономы и математики Гиппарх и Клавдий Птолемей (II в до н.э) нашли зависимость между сторонами и углами треугольника, Гиппарху часто приписывают авторство первых тригонометрических таблиц, не дошедших до нас. Вместо современной функции синуса Гиппарх и другие древнегреческие математики обычно рассматривали зависимость длины хорды окружности от  центрального угла (дуги окружности, выраженной в угловой мере). 

     В IV веке, после упадка античной науки, центр развития математики переместился в Индию. В 4-5 веках индийский ученый Ариабхаты ввел специальный термин джива – «тетива», который при переводе арабских текстов на латынь был заменен синусом, что означает изгиб, кривизна.

Под «джива» понималась длина отрезка AD, опирающегося на дугу AC окружности радиуса R=3438 единиц  Таким образом, «индийский синус» угла в 3438 раз больше современного синуса.

     Индийцы первыми ввели в использование косинус -  «дополнительный синус».

     В VIII веке учёные стран Ближнего и Среднего Востока познакомились с трудами древнегреческих и индийских математиков и астрономов. Самые ранние из сохранившихся трудов принадлежат ал-Хорезми и ал-Марвази (IX век), которые рассмотрели, наряду с известными ещё индийцам синусом и косинусом, новые тригонометрические функции: тангенс, котангенс, секанс и косеканс. Из-за отсутствия алгебраической символики все теоремы выражались в громоздкой словесной форме, но по существу были  эквивалентны их современному пониманию.

     Первая книга в Европе, в которой тригонометрия рассматривалась как самостоятельная дисциплина появилась в XV в. Её написал немецкий астроном и математик Региомонтан (И.Мюллер) .

     К концу XVII века появились современные названия тригонометрических функций. Термин «синус» впервые употребил около 1145 года английский математик и арабист Роберт Честерский. Региомонтан в своей книге назвал косинус «синусом дополнения»,его последователи в XVII веке сократили это обозначение до co-sinus (Эдмунд Гунтер) а позднее — до cos английский математик , изобретатель логарифмической линейки Уильям Отред. Названия тангенса и секанса предложил в 1583 году датский математик Томас Финке, а английский математик и астроном Эдмунд Гунтер ввёл названия котангенса и косеканса.Термин «тригонометрические функции» впервые употребил в своей «Аналитической тригонометрии» (1770) немецкий математик и физии Георг Симон Клюгель

     Современные обозначения синуса и косинуса знаками sin x и cos x были впервые введены в 1739 году И. Бернулли в письме к петербургскому математику Л. Эйлеру. Эйлер принял эти обозначения и стал употреблять их в своих работах. Кроме того, Эйлер ввел следующие  обозначения тригонометрических функций угла x: tang x, cot x, sec x, cosec x.      

– Закрепление нового материала

Учитель:

Французский философ, писатель и мыслитель 18 века Жан Жак Руссо говорил, что час работы научит больше, чем день объяснения.

Переходим к решению задач.

Работа по решению задач идет у доски с вызовом обучающихся и на местах.                                                                                 

Примеры:

Найти значение выражения:

1.     

ищем значения в таблице и подставляем в пример

2.  

3.    

–  Подведение итогов

1) Достижение предметных и метапредметных  результатов.

Учитель:

Что нового узнали сегодня на уроке?

Чему Вы научились?

Что вызвало затруднение?

Ответы обучающихся:

2) Учитель:

Подсчитайте количество баллов и оцените свою работу.

Сверим с моим мнением. 

–  Домашние задание 

Спасибо за работу!