Площадь криволинейной трапеции. Вычисление интегралов

Электронные таблицы «Microsoft Excel»

Лабораторная работа  «Площадь криволинейной трапеции. Вычисление интегралов». 

Темы: «Логические функции», «Функции категории "Проверка свойств и значений"»

Немного математики. Общие сведения

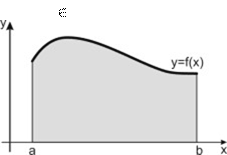Определение. Криволинейной трапецией называется фигура, ограниченная графиком непрерывной неотрицательной функции y=f(x), x [a,b], прямыми x=a, y=b и отрезком оси Ох (рис. 1).

Рис. 1. Криволинейная трапеция

Существует ряд формул, позволяющих вычислить приближенное значение площади криволинейной трапеции. 1. Формула трапеций. 

Разделим отрезок [a,b] на n равных частей точками: a=х₀, х₁, х₂, …, х_n=b (рис. 2). 

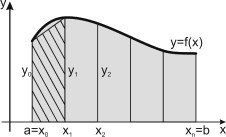
Рис. 2. Графическая иллюстрация метода трапеций

В этом случае шаг разбиения h=(b-a)/n.

На каждом участке разбиения [х_i, х_i+1] (i=0, 1, 2,…, n-1) площадь криволинейной трапеции заменим площадью трапеции. 

Так на участке [х0, х1]: 

(1)

Распространяя формулу на все отрезки разбиения, получим общую формулу трапеций для отрезка [a,b].

(2)

Очевидно, что чем меньше шаг разбиения, тем меньше разность между площадью криволинейной и обычной трапецией.

Данная формула дает один из простейших способов вычисления определенного интеграла и называется формулой трапеций.  

2.  Формула Симпсона.

Если считать, что n-четное (n=2m), то, можно использовать более точную (по сравнению с формулой трапеций) формулу Симпсона:

(3)

3.  Метод Монте-Карло.

Разобьем интервал [a,b] на n частей случайным образом, тогда 

(4)

x_i – случайные точки, лежащие в интервале [a,b]. 

Для получения таких точек на основе последовательности случайных точек, равномерно распределенных в интервале [0,1] достаточно воспользоваться формулой: x_i = a+(b-a) СЛЧИС().

Полученные формулы (2), (3), (4) являются формулы приближенного вычисления определенно-

го интеграла .

Компьютерный практикум

Задание. Построить график и вычислить площадь криволинейной трапеции, ограниченной линиями y=x²sin x, y=0, x=a, x=b (a<b) тремя способами: по формуле трапеций; по формуле Симпсона; методом Монте-Карло. Решение

Вариант построения таблицы на рис. 3. 

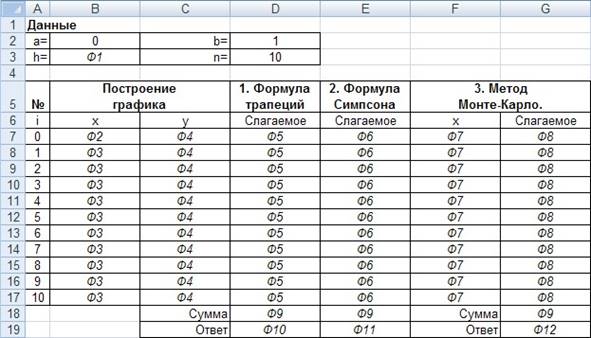
Рис. 3. Вариант построения рабочего листа

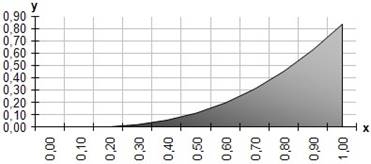
Рис. 4. График криволинейной трапеции

Комментарии к таблице:

Ответы

1.             Формула Ф1 (ячейка В3) – вычисление шага разбиения:  =($D$2-$B$2)/$D$3

2.             Формула Ф2 (ячейка В7) – ссылка на начальную точку отрезка:             =$B$2

3.             Формула Ф3 (ячейка В8, размножить в ячейки диапазона B9:В17) – вычисление следующего значения х: 

=B7+$B$3 4.    Формула Ф4 (ячейка С7, размножить в ячейки диапазона С8:С17) – вычисление y по заданному х: =B7^2*SIN(B7)

5.             Формула Ф5 (ячейка D7, размножить в ячейки диапазона D8:D17) – вычисление слагаемого в формуле трапеций (2): 

=ЕСЛИ(ИЛИ(A7=0;A7=$D$3);B7^2*SIN(B7)/2;B7^2*SIN(B7))

6.             Формула Ф6 (ячейка E7, размножить в ячейки диапазона E8:E17) –вычисление слагаемого в формуле Симпсона (3): 

=ЕСЛИ(ИЛИ(A7=0;A7=$D$3);B7^2*SIN(B7)/2;ЕСЛИ(ЧЁТН(A7)=A7;B7^2*SIN(B7); 2*B7^2*SIN(B7)))

7.             Формула Ф7 (ячейка F7, размножить в ячейки диапазона F8:F17) – вычисление случайного значения х: 

=$B$2+($D$2-$B$2)*СЛЧИС()

8.             Формула Ф8 (ячейка G7, размножить в ячейки диапазона G8:G17) – вычисление y по заданному х:    

=$F7^2*SIN($F7)

9.             Формула Ф9 (ячейка D18, размножить в ячейки E18 и G18) – нахождение суммы всех полученных слагаемых:  

=СУММ(D7:D17)

10.         Формула Ф10 (ячейка D19) – вычисление по формуле (2):           =$B$3*D18

11.         Формула Ф11 (ячейка E19) – вычисление по формуле (3):           =2*$B$3/3*E18

12.         Формула Ф12 (ячейка F19) – вычисление по формуле (4):           

=($D$2-$B$2)/($D$3+1)*G18