«Площадь многоугольников»

Открытый урок геометрии в 8 классе

Тема: Площадь многоугольников

Цель: повторить, закрепить, обобщить и систематизировать знания учащихся по теме, совершенствовать навыки поиска путей решения задач  на вычисление площадей фигур; развивать логическое мышление, творческие способности, внимание, умение создавать математические модели к задачам; воспитывать чувства коллективизма, интерес к изучению геометрии.

Задачи:

образовательные :

1.     формировать навыки самостоятельного воспроизведения ранее полученных знаний;

2.     формировать навыки использования полученных знаний по теме площадь многоугольников в жизненных ситуациях;

развивающие:

1.     развитие мышления обучающихся, развитие математической речи;

2.     развитие коммуникативных умений и интеллектуальных способностей посредством взаимодействия в процессе выполнения заданий;

воспитательные:

1.     воспитание способностей к нравственному общению среди обучающихся, к сотрудничеству, то есть формирование коммуникативных навыков;

2.     воспитание ответственности, организованности.

Тип урока: обобщение и систематизация знаний .

Оборудование: мультимедийная доска, индивидуальные карточки, кроектор, компьютер.

Методы: проблемно -поисковый метод

Формы познавательной деятельности учащихся: групповая, индивидуальная, коллективная.

Структура  урока:

1.     Организационный момент

2.     Мотивация выбора данной темы

3.     Актуализация опорных знаний и их коррекция

4.     Физкультминутка

5.     Мозговой штурм

6.     Информация о домашнем задании и подведение итогов.

7.     Рефлексия

 

 

 

 

 

 

План урока:

1.     Организационный момент.

Подготовка учащихся к работе на занятии

Здравствуйте ребята. Посмотрите на друг друга, улыбнитесь, порадуйтесь солнечному дню.

     2.Мотивация выбора данной темы

Тема нашего урока: Площадь многоугольников. Запишите в тетради число и тему урока.

Слайд 2

Эпиграф

Среди равных умов при одинаковости прочих условий превосходит тот, кто знает геометрию.

Б.Паскаль

3.Актуализация опорных знаний и их коррекция

Экспресс-опрос

(Учитель проектирует вопросы экспресс опроса на экран)

Слайд 3

1.     Сформулируйте определение многоугольника

2.     какие виды многоугольников вы изучили?

3.     Что такое площадь многоугольника?

4.     Какие единицы измерения площадей вы знаете?

Слайд 4

Составь пару

На экран проектируют геометрические фигуры и формулы вычисления площадей. Учащиеся должны составить пару: геометрическая фигура и формула, с помощью которой вычисляется ее площадь.

 

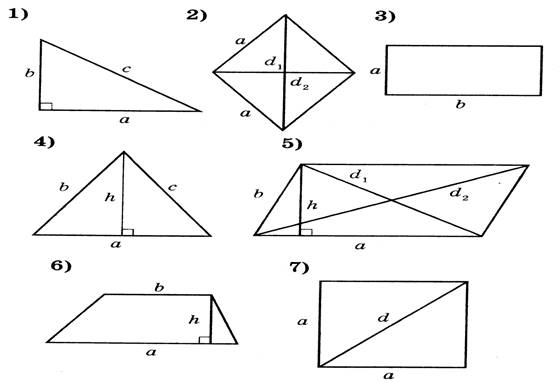
А) S =;    Б) S = ab;    В) S = ;   Г) S = ah ; Д) S = ;

E) S = ab ; Ж) S = ah.

Учитель проектирует на экран ответ: 1-Е; 2-А; 3-Б; 4-Ж; 5-Г; 6-В;  7-Д.

Слайд 5

Решение устных упражнений

1)    Найдите площадь трапеции, основания которой равны 2см и 8см, а высота – 5 см.

а) 50 см² ;б) 80 см²; в) 25 см²; г)15 см²

2)    Найдите площадь ромба, диагонали которого равны 4 см и 6 см.

 а) 24 см² ;б) 8 см²; в) 20 см²; г)12 см²

3)    Высота параллелограмма со стороной а и площадью S равна …

а) a*S ;б) a:S ; в) S:а; г) 2S :а

4)    Стороны квадратов относятся как  2:5. Как относятся площади этих квадратов?

а) 2:5 ;б) 4:25; в) 2:25; г) 4:5

5)    Площадь равнобедренного прямоугольного треугольника с катетом 2а равна…

а)  а² ;б) 2а²; в) 4а²; г)8а²

На экран учитель проектирует правильные ответы.

1)в ; 2) г; 3)в; 4)б; 5)б

Работа с карточками

Трое учащихся у доски решают задачи, записанные на карточках ( задачи разных уровней сложности; остальные самостоятельно выбирают задачу для решения)

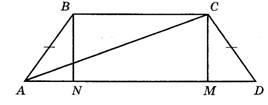Дано: АD = 50 cм;BC = 14см;AC = 40 см

 

Вычислить: .

 

Решение :

= * CM

NM+MD=AD-NM=50-14=36 (см).

Поскольку AN=MD, то MD=18 (см)

AM=AD-MD,AM=50-18=32(cм)

Из ∆ АСМ (∠M=90º):СМ²=АС²-АМ²,

СМ²=40²-32², СМ= = 24(см)

=*24 =768( см²)

Ответ:768см²

 

 

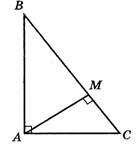 Дано: ВМ=16 см;МС=9 см.

Вычислить:

Решение : =ВС*АМ.

ВС=ВМ+МС, ВС=16+9=25( см)    АМ²=ВМ*МС

 

(высота прямоугольного треугольника, проведенная к гипотенузе, есть среднее пропорциональное отрезков, на которые эта высота делит гипотенузу).

Значит, АМ²=16*9=144, АМ=12 см., Тогда =*25*12=150( см²)

Ответ: 150 см²

 

Карточка№3

Диагонали ромба относятся как 3:4, а его сторона равна 25 см. Вычислите площадь ромба.

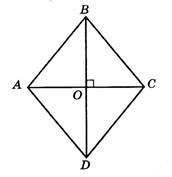Дано:АВ:BD; ВС=25 см.

Вычислить:

Решение

=AC*BD

OC:BD=1,5:2

(поскольку диагонали ромба точкой пересечения делятся пополам)

Пусть одна часть равна х, тогда ОС=1,5х, ОВ=2х.

Треугольник ВОС прямоугольный (поскольку диагонали ромба перпендикулярны). По теореме Пифагора :ВС²=ОС²+ОВ².

Имеем : 25²=(1,5х)² + (2х)²

                      625=2,25х²+4х²

                  625=6,25х²

               х²=625:6,25

                х²=100

                 х=10

 

Значит , ОС=1,5*10=15 см, а ОВ=2*10=20 см, Тогда АС=2*ОС=2*15=30 см

BD= 2*OB=2*20=40 см.

 Вычисляем площадь ромба:

=*30*40=600 см²

Ответ: 600 см²

Учащиеся, которые работали у доски, комментируют решение задач.

 

Решение задач практического содержания

Учащиеся объединяются в группы. Каждая группа осуждает путь решения задачи.  Все предложения осуждаются коллективно.

Задача

Поле имеет форму параллелограмма, большая сторона которого равна 500 м, а высота 180 м. Через это поле под прямым углом к большей стороне проходит шоссе шириной 12м. Определите посевную площадь поля .

 

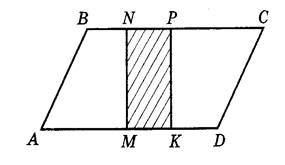
Учащиеся составляют математическую модель задачи.

1.     Найти площадь параллелограмма АВСD (то есть площадь всего поля)

2.     Найти площадь прямоугольника MNPK ( то есть площадь дороги, которая проходит через поле)

3.     Найти разность площадей параллелограмма  АВСD и прямоугольника MNPK  (то есть искомую площадь)

Решение

1.    =AD*MN

= 500*180 = 90000 (м²)

2.    = MN*PK, = 180*12=2160 м²

3.    S=- , S=90000-2160 = 87840 м² = 8,784 га

Ответ. 8,874 га

 

4.Физкультминутка

Много ль надо нам, ребята

Много ль надо нам, ребята, Для умелых наших рук? Нарисуем два квадрата, А на них огромный круг, А потом еще кружочек, Треугольный колпачок. Вот и вышел очень, очень Развеселый чудачок.

(Дети рисуют в воздухе геометрические фигуры.)

 

4.     Мозговой штурм

Слайд 8

Знания полученные при изучении темы «Многоугольники и их площади», широко используют в черчении, рисовании , в строительстве и архитектуре, а также в повседневной жизни. Например, чтобы обложить плиткой пол, необходимо уметь вычислить площадь пола, площадь одной плитки и подсчитать, сколько плитки нужно приобрести.

     Слайд 9

Предлагаю поделить класс на 3 бригады, каждая из которых получает наряд-задание. ( у каждой бригады рулетка для выполнения  измерительных работ)

1.     Рассчитать нужное количество плитки для покрытия пола в классе и необходимую для этого сумму денег, если цена одной плитки размером 0,3м  х  0,3м, равна 32 руб.

2.     Рассчитать нужное количество краски для покраски 6 столов в классе и необходимую для этого сумму денег, если на 1кв.м требуется 150 г. краски по цене 95 руб. за 1 кг.

3.     Рассчитать нужное количество обоев для покрытия стен в классе и необходимую для этого сумму денег, если 1 рулон длиной 10 м. и шириной 50 см стоит 105 руб.

Слайд 10

Сдача работы

Бригада	площадь	количество товара	цена за ед.	Сумма
1	пола 26,84 кв.м.	300 шт. паркетной плитки	32 руб.	9600 руб.
2	столов 4,32 кв.м.	0,65 кг. краски	95 руб.	61,75 руб.
3	стен 36,7 кв.м	8 рулонов обоев	105 руб.	840 руб.
Итого				10501,75 руб.

 

Каждая группа решила свои задачи и рассказала о них

6.Информация о домашнем задании и подведение итогов.

 

 

Домашним заданием для вас будет: найти площадь, которую занимает мебель в гостиной комнате.

 

7.Рефлексия

Слайд 11

В течении урока поработали неплохо, особенно хотелось бы отметить…

Эту оценку дала я вам, а теперь оцените сами нашу работу.

Ответьте на вопросы:

·        Что нового я узнал?

·        Пригодятся ли на практике мне эти знания?

·        Где я смогу применить эти знания?

Список литературы

1)    Геометрия. 7-9 классы: учеб. для общеобразоват. учреждений  / Л.С. Атанасян, В.Ф. Бутузов , С.Б.Кадомцев и др. – 20-е изд.- М. : Просвещение ,2010.

2)    Атанасян Л.С., В.Ф. Бутузов, Глазков Ю.А., Юдина И.И. Геометрия. Рабочая тетрадь, 8 класс . Пособие для учащихся общеобразовательных учреждений .- М. : ОАО «Издательство Просвещение» 2006.

3)    Учительский портал http://www.uchportal.ru

4)    Фестиваль педагогических идей «Открытый урок» http://festival.1september.ru

 

Скачано с www.znanio.ru