
ПЛОЩАДЬ ПАРАЛЛЕЛОГРАММА.
Цели: вывести формулу для вычисления площади параллелограмма; научить применять формулы при решении задач.
Ход урока
I. Проверка домашнего задания.
Выполнить задания (устно):
1. SАВСD – ?
|
2. ВМ = 5, МС = 4 SАВСD – ? |
|
3. |
Площадь прямоугольника АВСD = 20 см2. Найти площадь параллелограмма МВСK.
II. Изучение нового материала.
1. Ввести понятие «высота параллелограмма к данной стороне».
2. При выведении формулы площади параллелограмма целесообразно написать на доске формулу S = а · ha и продемонстрировать соответствующий рисунок, а затем провести силами учащихся доказательство формулы.
III. Закрепление изученного материала.
№№ 459 (а) (устно), 459 (б, в), 464 (в).
|
|
АВ : ВС = 3 : 7, РАВСD
= 120, Найти: SАВСD. |
IV. Самостоятельная работа (обучающего характера).
Вариант I
Стороны параллелограмма 10 см и 6 см, а угол между этими сторонами 150°. Найдите площадь этого параллелограмма.
Вариант II
Острый угол параллелограмма равен 30°, а высоты, проведенные из вершины тупого угла, равны 4 см и 3 см. Найти площадь параллелограмма.
Вариант III
Найдите площадь ромба, диагонали которого равны 8 см и 6 см. Проверить решение с помощью закрытой доски:
Вариант I
|
|
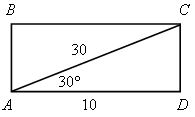
1. 2.
Катет АЕ лежит против угла 30°, поэтому АЕ = 3. SАВСD = ВС · АЕ = 10 · 3 = 30 см2. |
Вариант II
|
|
1. Катет ВМ лежит против угла в 30°, поэтому АВ = 2ВМ = 6 см. 2. SАВСD = ВK · DС = 8 · 6 = 48 см2. |
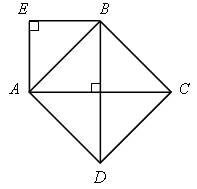
Вариант III
Использовать
задание 3 из домашней работы. ВО = ОD = 4 см,
АО = ОС = 3 см.
SАЕВО = 3 · 4 = 12.
SАВСD = 12 · 2 = 24.
Подвести учащихся к выводу, что площадь ромба равна половине произведения его диагоналей.
V. Итоги урока.
|
|
|
|
|
S = а · b
|
S = а · ha
|
S = S = а · h |
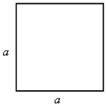
S = а2
 Домашнее задание: § 2, вопрос 4, с. 133; №№ 459 (в,г),
460,462, 464 (б).
Домашнее задание: § 2, вопрос 4, с. 133; №№ 459 (в,г),
460,462, 464 (б).
Для желающих.
Найдите углы параллелограмма, если его площадь равна 20 см2, а высота, проведенная из вершины тупого угла, делит одну из сторон на отрезки 2 см и 8 см, считая от вершины острого угла.
Ответ: 45°; 135°.
2. Сравните площади параллелограмма и прямоугольника, если они имеют одинаковые основания и одинаковые периметры.
Ответ: площадь прямоугольника больше площади параллелограмма.
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.