ПОБУДОВА ТА ВИКОРИСТАННЯ ВИРОБНИЧИХ ФУНКЦІЙ Опис методу лабораторної роботи

ПОБУДОВА ТА ВИКОРИСТАННЯ ВИРОБНИЧИХ ФУНКЦІЙ

Опис методу лабораторної роботи

          Під виробничою функцією розуміють економіко-математичне рівняння, яке зв’язує випуск продукції та витрати ресурсів на цей випуск. Двочинникова виробнича функція має вигляд

                                               .                                             (3.1)                           

Тут змінні характеризують такі фактори: K - обсяг виробничих фондів у вартісному або натуральному виразі (вартість або кількість обладнання), L - обсяг трудових ресурсів (кількість робітників, кількість людино-днів) , Y - обсяг продукції (валової) у вартісному або натуральному виразі або обсяг послуг у вартісному виразі.

У лабораторній роботі розглядаються виробничі функції:

1. степенева,

, , ,              (3.2)

2. Кобба - Дугласа

, ,;                     (3.3)

         Ця функція з’явилась у 40-і роки ХХ століття. Американські вчені Кобб та Дуглас вирішили оцінити значення  функції (3.2), використовуючи

дані американської обробляючої промисловості за період з 1899 по 1922 роки – на основі аналізу індексів виробництва, основного капіталу та праці. В результаті вчені зробили висновок, що  . Нову функцію назвали виробничою функцією Кобба-Дугласа. 

3. Кобба - Дугласа з урахуванням науково-технічного прогресу

, , ,                  (3.4)

де - індекс науково-технічного прогресу, Т – час.

Після логарифмування по натуральній основі степенева виробнича функція (3.2) має вигляд

.                             (3.5)

Функція Кобба – Дугласа перетвориться у функцію виду

 де .                     (3.6)

Тому рівняння регресії приймає простий вид

.                                   (3.7)

Функція (3.4) може бути перетворена до виду

,                                          (3.8)

звідкіля, приймаючи в увагу, що , рівняння регресії може бути записане так

.                               (3.9)

         Усі функції (3.5) ,(3.7), (3.9) являють собою лінійні рівняння відносно , . Значення параметрів  , можна оцінити за допомогою лінійного регресійного аналізу по методу найменших квадратів на основі використання статистичних даних.

Використовуючи елементи матричної алгебри, рівняння (3.5) і  (3.9) можна записати у виді

                                      ,                  (3.10)           

де  - результативна ознака, - чинникові ознаки, -                залишок або випадкове відхилення, - параметри рівняння, n – кількість спостережень. Тут результативною ознакою виступає обсяг продукції або послуг, чинниковими ознаками є обсяг виробничих фондів і обсяг трудових ресурсів.

Рівняння (3.7) в позначеннях матричної алгебри має вигляд

                                      ,                                (3.11)     

Для переходу від рівняння (3.5) до рівняння (3.10) вводяться заміни

.        (3.12)

Для переходу від рівняння (3.9) до рівняння (3.10) вводяться такі заміни

        ,      (3.13)

Перехід від рівняння (3.7) до рівняння (3.11) здійснюється через позначення

                     .                      (3.14)

Значення параметрів рівняння можна знайти по формулі (3.15)

.                                      (3.15)

Для цього необхідно виконати такі етапи:

а) обчислити ( );

б) знайти визначник ;

в) знайти мінори матриці ( );

г) знайти алгебраїчні доповнення матриці ( ), побудувати матрицю ( ), приєднану до ( );

д) побудувати транспоновану матрицю ;

е) знайти обернену матрицю ( )^-1= ;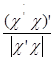

ж) знайти вектор ( );

з) визначити вектор      .     

Перший стовпець матриці х завжди одиничний, тому що модель має вільний член b₀, інші стовпці цієї матриці - це чинникові ознаки.      

Як міру адекватності регресійної моделі часто використовують коефіцієнт детермінації. Останній задається формулою

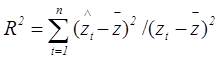,                                    (3.16)

де - теоретичні значення результативної ознаки,

                                  ,                                               (3.17)

або

                                             ,                                                    (3.18)

 а  - середньоарифметичне значення результативної ознаки.

Позитивне значення квадратного кореня з коефіцієнта детермінації називається коефіцієнтом кореляції. Чим більше значення , тим вище степінь адекватності рівняння регресії. Однак у показника  є недолік, бо великі значення коефіцієнта можуть досягатися завдяки малому числу спостережень. Мірою адекватності моделі, покликаної виправити цей недолік, є скорегований коефіцієнт детермінації, що задається формулою

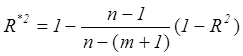.                                   (3.19)

Міра автокореляції випадкової величини , як правило, оцінюється коефіцієнтом Дарбіна - Уотсона

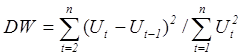.                         (3.20)

При значенні DW, близькому до 2, говорять, що автокореляція відсутня (ситуація, що, власне, і є бажаною).

Якщо у побудовану виробничу функцію підставити чинникові ознаки, то можна визначити очікуване значення випуску продукції.

3.4 Порядок виконання роботи та методичні вказівки з її виконання

Побудова та використання виробничих функцій реалізується за допомогою програмного забезпечення, розробленого в середовищі Delphi 5.0. Для запуску програми необхідно ввести пароль.  Екранна форма, що відкривається, дає можливість побудувати виробничі функції: степеневу, Кобба-Дугласа, Кобба-Дугласа з урахуванням НТП. При побудові степеневої функції відкривається вікно, яке дає можливість ввести початкові дані            (рисунок 3.1).

Клавіша „Рассчитать ” дозволяє вивести на екран монітора параметри цієї виробничої функції (рисунок 3.2).

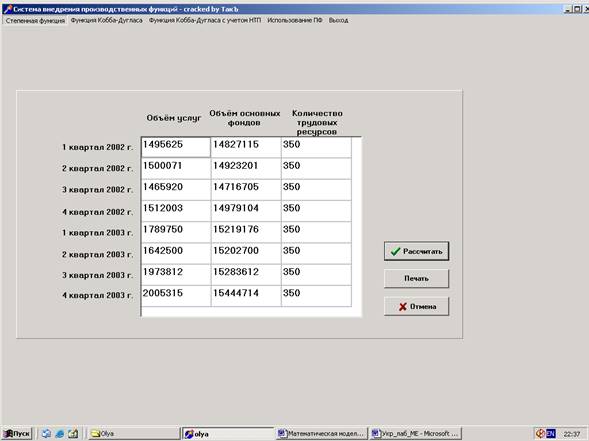
      Рисунок 3.1- Екранна форма для введення початкових даних

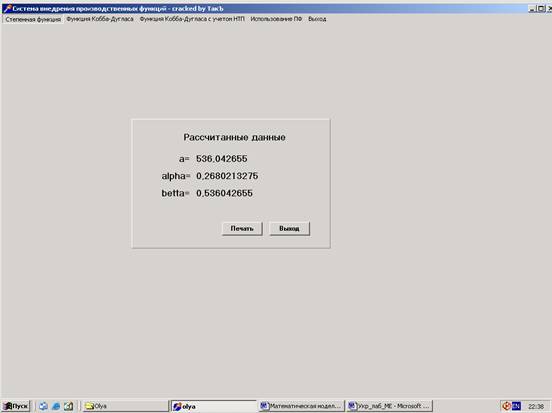
     Рисунок 3.2- Екранна форма із визначеними параметрами степеневої виробничої функції

          Клавіша „Проверка адекватности модели” дозволяє одержати інформацію для аналізу побудованої функції. Екранна форма, на якій показані коефіцієнти: кореляції, детермінації та Дарбіна-Уотсона наведена на рисунку 3.3.

          Аналогічно за початковими даними можна побудувати та оцінити виробничі функції Кобба-Дугласа без урахування та з урахуванням НТП.

           Для використання виробничої функції Кобба-Дугласа необхідно ввести значення обсягів основних виробничих фондів, трудових ресурсів та параметри моделі (рисунок 3.4). Для введення цих даних використовується кома. За цими даними можна одержати обсяг випуску продукції або послуг, позначений через Х. Аналіз величини Х дає можливість визначити доцільність збільшення або зменшення обсягів основних виробничих фондів та трудових ресурсів.

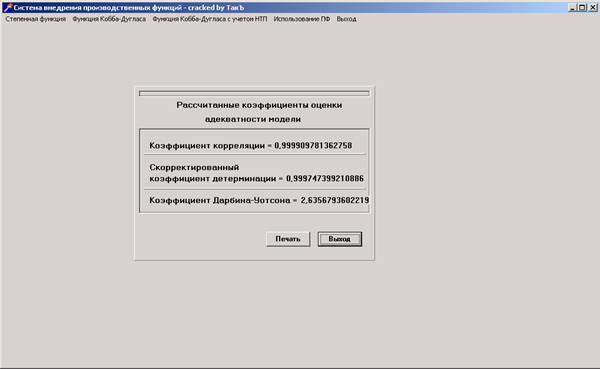
  Рисунок 3.3 – Екранна форма для оцінювання адекватності моделі     

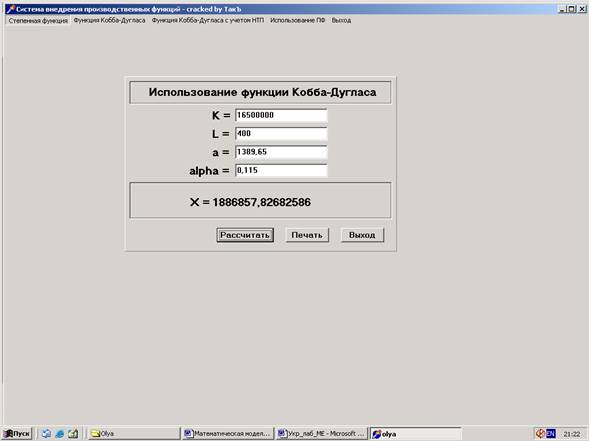
Рисунок 3.4 – Екранна форма для використання функції Кобба-Дугласа

-