Подборка заданий ЕГЭ по теме "Пирамида"

данный материал представляет собой подборку заданий из банка заданий ЕГЭ по теме "Пирамида". Может использоваться для работы в 11 классе на уроке, для индивидуальной работы, для контроля знаний по данной теме: составления тестов, контрольных работ. Задания направлены на контроль прочности усвоения как самого понятия пирамиды, её элементов, так и формул для вычисления её площади поверхности, объёма. Включают в себя все возможные задания ЕГЭ по данной теме. Прилагаются и решения всех задач. Данный материал может использоваться и на уроках в других классах. Например при изучении темы "Теорема пифагора"(8 класс)

Задачи ЕГЭ по теме «Пирамида»

B 13 № 901. В правильной треугольной пирамиде медианы основания пересекаются в точке . Площадь треугольника равна 2; объем пирамиды равен 6. Найдите длину отрезка .

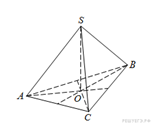
B 13 № 911. В правильной четырехугольной пирамиде точка – центр основания, – вершина, , . Найдите боковое ребро

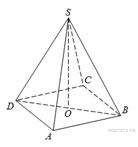
B 13 № 920. В правильной треугольной пирамиде точка – середина ребра , – вершина. Известно, что =3, а площадь боковой поверхности пирамиды равна 45. Найдите длину отрезка .

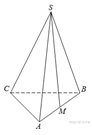
B 13 № 27074. Объем параллелепипеда равен 9. Найдите объем треугольной пирамиды .

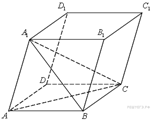
B 13 № 27085. Во сколько раз увеличится объем правильного тетраэдра, если все его ребра увеличить в два раза?

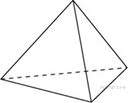
B 13 № 27089. Во сколько раз увеличится объем пирамиды, если ее высоту увеличить в четыре раза?

B 13 № 27113. Объем треугольной пирамиды , являющейся частью правильной шестиугольной пирамиды , равен 1. Найдите объем шестиугольной пирамиды.

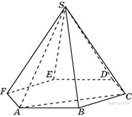
B 13 № 27114. Объем правильной четырехугольной пирамиды равен 12. Точка – середина ребра . Найдите объем треугольной пирамиды .

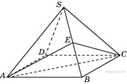
B 13 № 27115. От треугольной пирамиды, объем которой равен 12, отсечена треугольная пирамида плоскостью, проходящей через вершину пирамиды и среднюю линию основания. Найдите объем отсеченной треугольной пирамиды.

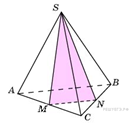
B 13 № 27131. Во сколько раз увеличится площадь поверхности правильного тетраэдра, если все его ребра увеличить в два раза?

B 13 № 27157. Во сколько раз увеличится площадь поверхности октаэдра, если все его ребра увеличить в 3 раза?

B 13 № 27172. Во сколько раз увеличится площадь поверхности пирамиды, если все ее ребра увеличить в 2 раза?

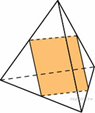
B 13 № 27175. Ребра тетраэдра равны 1. Найдите площадь сечения, проходящего через середины четырех его ребер.

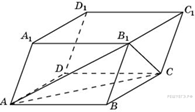
B 13 № 27182. Объем параллелепипеда равен 12. Найдите объем треугольной пирамиды .

B 13 № 27184. Объем куба равен 12. Найдите объем четырехугольной пирамиды, основанием которой является грань куба, а вершиной — центр куба.

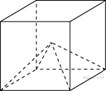
B 13 № 77154. Найдите объем параллелепипеда , если объем треугольной пирамиды равен 3.

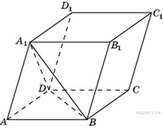
B 13 № 284351. В правильной треугольной пирамиде — середина ребра , — вершина. Известно, что, а . Найдите площадь боковой поверхности.

B 13 № 284356. В правильной треугольной пирамиде медианы основания пересекаются в точке . Объем пирамиды равен , . Найдите площадь треугольника .

----------------------------------------------------------------------------------------------------------------------------------------

Задачи ЕГЭ по теме «Пирамида»

B 13 № 27113. Объем треугольной пирамиды , являющейся частью правильной шестиугольной пирамиды , равен 1

B 13 № 27182. Объем параллелепипеда равен 12

Материалы на данной страницы взяты из открытых истончиков либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.

11.01.2017

Подборка заданий ЕГЭ по теме "Пирамида"

Задачи ЕГЭ по теме «Пирамида»

B 13 № 27113. Объем тре­уголь­ной пи­ра­ми­ды , яв­ля­ю­щей­ся ча­стью пра­виль­ной ше­сти­уголь­ной пи­ра­ми­ды , равен 1

B 13 № 27182. Объем па­рал­ле­ле­пи­пе­да равен 12

B 13 № 27113. Объем треугольной пирамиды , являющейся частью правильной шестиугольной пирамиды , равен 1

B 13 № 27182. Объем параллелепипеда равен 12