
Работа 1
Вариант 1
1.
Материальная точка
движется прямолинейно по закону ![]() , где
, где ![]() — расстояние от точки отсчета в метрах,
— расстояние от точки отсчета в метрах, ![]() — время в секундах, измеренное с начала движения. Найдите ее
скорость (в метрах в секунду) в момент времени
— время в секундах, измеренное с начала движения. Найдите ее
скорость (в метрах в секунду) в момент времени ![]() с.
с.
2.
Материальная точка движется
прямолинейно по закону ![]() , где
, где ![]() — расстояние от точки отсчета в метрах,
— расстояние от точки отсчета в метрах, ![]() — время в секундах, измеренное с начала
движения. Найдите ее скорость (в метрах в секунду) в момент времени
— время в секундах, измеренное с начала
движения. Найдите ее скорость (в метрах в секунду) в момент времени ![]() с.
с.
3.
Материальная точка
движется прямолинейно по закону ![]() , где
, где ![]() — расстояние от точки отсчета в метрах,
— расстояние от точки отсчета в метрах, ![]() — время в секундах, измеренное с начала
движения. Найдите ее скорость (в метрах в секунду) в момент времени
— время в секундах, измеренное с начала
движения. Найдите ее скорость (в метрах в секунду) в момент времени ![]() с.
с.
4.
Материальная точка движется прямолинейно
по закону ![]() , где
, где ![]() — расстояние от точки отсчета в метрах,
— расстояние от точки отсчета в метрах, ![]() — время в секундах, измеренное с начала движения. В какой
момент времени (в секундах) ее скорость была равна 14 м/с?
— время в секундах, измеренное с начала движения. В какой
момент времени (в секундах) ее скорость была равна 14 м/с?
5.
Материальная точка движется прямолинейно
по закону ![]() , где
, где ![]() — расстояние от точки отсчета в метрах,
— расстояние от точки отсчета в метрах, ![]() — время в секундах, измеренное с начала движения. В какой
момент времени (в секундах) ее скорость была равна 15 м/с?
— время в секундах, измеренное с начала движения. В какой
момент времени (в секундах) ее скорость была равна 15 м/с?
Вариант 2
1.
Материальная точка
движется прямолинейно по закону ![]() , где
, где ![]() — расстояние от точки отсчета в метрах,
— расстояние от точки отсчета в метрах, ![]() — время в секундах, измеренное с начала
движения. Найдите ее скорость (в метрах в секунду) в момент времени
— время в секундах, измеренное с начала
движения. Найдите ее скорость (в метрах в секунду) в момент времени ![]() с.
с.
2.
Материальная точка
движется прямолинейно по закону ![]() , где
, где ![]() — расстояние от точки отсчета в метрах,
— расстояние от точки отсчета в метрах, ![]() — время в секундах, измеренное с начала
движения. Найдите ее скорость (в метрах в секунду) в момент времени
— время в секундах, измеренное с начала
движения. Найдите ее скорость (в метрах в секунду) в момент времени ![]() с.
с.
3.
Материальная точка
движется прямолинейно по закону ![]() , где
, где ![]() — расстояние от точки отсчета в метрах,
— расстояние от точки отсчета в метрах, ![]() — время в секундах, измеренное с начала
движения. Найдите ее скорость (в метрах в секунду) в момент времени
— время в секундах, измеренное с начала
движения. Найдите ее скорость (в метрах в секунду) в момент времени ![]() с.
с.
4.
Материальная точка движется прямолинейно
по закону ![]() , где
, где ![]() — расстояние от точки отсчета в метрах,
— расстояние от точки отсчета в метрах, ![]() — время в секундах, измеренное с начала движения. В какой
момент времени (в секундах) ее скорость была равна 4 м/с?
— время в секундах, измеренное с начала движения. В какой
момент времени (в секундах) ее скорость была равна 4 м/с?
5.
Материальная точка движется прямолинейно
по закону ![]() , где
, где ![]() — расстояние от точки отсчета в метрах,
— расстояние от точки отсчета в метрах, ![]() — время в секундах, измеренное с начала движения. В какой
момент времени (в секундах) ее скорость была равна 3 м/с?
— время в секундах, измеренное с начала движения. В какой
момент времени (в секундах) ее скорость была равна 3 м/с?
Работа 2
Вариант 1
1.
Прямая ![]() параллельна касательной к
графику функции
параллельна касательной к
графику функции ![]() .
.
Найдите абсциссу точки касания.
2.
Прямая ![]() является касательной к графику функции
является касательной к графику функции ![]() .
.
Найдите абсциссу точки касания.
3.
На рисунке изображены график функции ![]() и касательная к нему в точке с
и касательная к нему в точке с
абсциссой ![]() . Найдите значение производной функции
. Найдите значение производной функции ![]() в точке
в точке ![]() .
.

4. На рисунке изображены график функции ![]() и касательная к нему в точке с
абсциссой
и касательная к нему в точке с
абсциссой ![]() .
Найдите значение производной функции
.
Найдите значение производной функции ![]() в точке
в точке ![]() .
.
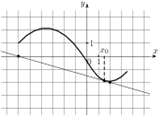
5. На
рисунке изображены график функции ![]() и
касательная к нему в точке с абсциссой
и
касательная к нему в точке с абсциссой ![]() . Найдите значение производной
функции
. Найдите значение производной
функции ![]() в точке
в точке ![]() .
.
Работа 2
Вариант 2
1.
Прямая ![]() параллельна касательной к
графику функции
параллельна касательной к
графику функции ![]() .
.
Найдите абсциссу точки касания.
2.
Прямая ![]() является касательной к графику функции
является касательной к графику функции ![]() .
.
Найдите абсциссу точки касания.
3.
На рисунке изображены график функции ![]() и касательная к нему в точке с
и касательная к нему в точке с
абсциссой ![]() .
Найдите значение производной функции
.
Найдите значение производной функции ![]() в точке
в точке ![]() .
.

4. На рисунке изображены график функции ![]() и касательная к нему в точке с
абсциссой
и касательная к нему в точке с
абсциссой ![]() .
Найдите значение производной функции
.
Найдите значение производной функции ![]() в точке
в точке ![]() .
.

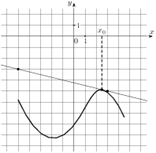
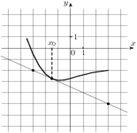
5. На рисунке изображены график функции ![]() и касательная к нему в точке с
абсциссой
и касательная к нему в точке с
абсциссой ![]() .
Найдите значение производной функции
.
Найдите значение производной функции ![]() в точке
в точке ![]() .
.
Работа 3 Вариант 1
1.
На рисунке изображен график функции ![]() , определенной на интервале
, определенной на интервале ![]() . Найдите сумму точек
экстремума функции
. Найдите сумму точек
экстремума функции ![]() .
.

2.
На рисунке изображён график ![]() — производной функции
— производной функции ![]() , определенной на интервале
, определенной на интервале ![]() . В какой точке отрезка
. В какой точке отрезка ![]() функция
функция ![]() принимает наибольшее значение?
принимает наибольшее значение?

3.
На рисунке изображен график ![]() — производной функции
— производной функции ![]() , определенной на интервале
, определенной на интервале ![]() . Найдите количество точек
максимума функции
. Найдите количество точек
максимума функции ![]() , принадлежащих
отрезку
, принадлежащих
отрезку ![]() .
.

4.
На рисунке изображен график ![]() — производной функции
— производной функции ![]() , определенной на интервале
, определенной на интервале ![]() . Найдите промежутки
убывания функции
. Найдите промежутки
убывания функции ![]() . В
ответе укажите сумму целых точек, входящих в эти промежутки.
. В
ответе укажите сумму целых точек, входящих в эти промежутки.

5.
На рисунке изображен график ![]() —
производной функции
—
производной функции ![]() , определенной на интервале
, определенной на интервале ![]() . Найдите точку экстремума функции
. Найдите точку экстремума функции ![]() ,
принадлежащую отрезку
,
принадлежащую отрезку ![]() .
.

Работа 3 Вариант 2
1.
На рисунке изображен график функции ![]() , определенной на интервале
, определенной на интервале ![]() . Найдите сумму точек
экстремума функции
. Найдите сумму точек
экстремума функции ![]() .
.

2.
На рисунке изображён график ![]() — производной функции
— производной функции ![]() , определенной на интервале
, определенной на интервале ![]() . В какой точке отрезка
. В какой точке отрезка ![]() функция
функция ![]() принимает наибольшее значение?
принимает наибольшее значение?

3.
На рисунке изображен график ![]() — производной функции
— производной функции ![]() , определенной на интервале
, определенной на интервале ![]() . Найдите количество точек
максимума функции
. Найдите количество точек
максимума функции ![]() ,
принадлежащих отрезку
,
принадлежащих отрезку ![]() .
.

4.
На рисунке изображен график ![]() —
производной функции
—
производной функции ![]() , определенной на интервале
, определенной на интервале ![]() . Найдите промежутки убывания функции
. Найдите промежутки убывания функции ![]() . В ответе
укажите сумму целых точек, входящих в эти промежутки.
. В ответе
укажите сумму целых точек, входящих в эти промежутки.

5.
На рисунке изображен график ![]() —
производной функции
—
производной функции ![]() , определенной на интервале
, определенной на интервале ![]() . Найдите точку экстремума функции
. Найдите точку экстремума функции ![]() ,
принадлежащую отрезку
,
принадлежащую отрезку ![]() .
.

Работа 4
Вариант 1
1.
Найдите точку минимума функции ![]() .
.
2.
Найдите точку минимума функции ![]() .
.
3.
Найдите наибольшее значение функции ![]() на отрезке
на отрезке ![]() .
.
4.
Найдите наименьшее значение функции ![]() на
отрезке
на
отрезке ![]() .
.
5.
Найдите наибольшее значение функции ![]() на отрезке
на отрезке ![]() .
.
Работа 4
Вариант 2
1.
Найдите точку максимума функции ![]() .
.
2.
Найдите точку минимума функции ![]() .
.
3.
Найдите наибольшее значение функции ![]() на
отрезке
на
отрезке ![]()
4.
Найдите наименьшее значение функции ![]() на отрезке
на отрезке ![]() .
.
5.
Найдите наибольшее значение функции ![]() на отрезке
на отрезке ![]() .
.
Ответы
Работа 1
|
|
Вариант 1 |
Вариант 2 |
|
1 |
6 |
2 |
|
2 |
50 |
74 |
|
3 |
24 |
98 |
|
4 |
8 |
8 |
|
5 |
2 |
2 |
Работа 2
|
|
Вариант 1 |
Вариант 2 |
|
1 |
1,5 |
-4 |
|
2 |
0 |
1 |
|
3 |
0,5 |
0,25 |
|
4 |
-0,25 |
-0,25 |
|
5 |
-0,25 |
-0,5 |
Работа 3
|
|
Вариант 1 |
Вариант 2 |
|
1 |
|
|
|
2 |
|
|
|
3 |
|
|
|
4 |
|
|
|
5 |
|
|
Работа 4
|
|
Вариант 1 |
Вариант 2 |
|
1 |
|
|
|
2 |
|
|
|
3 |
|
|
|
4 |
|
|
|
5 |
|
|
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.