Подготовка к ГВЭ и ЕГЭ. Четырехугольники. 11 класс.

Четырехугольники и их свойства.

Разобрать решенные  задачи и выполнить самостоятельную работу.

Трапеция.

Задача 1. Основания трапеции равны 18 и 6, боковая сторона, равная 7, образует с одним из оснований трапеции угол 150°. Найдите площадь трапеции.

Решение.

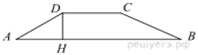
Введём обозначения, как показано на рисунке. Площадь трапеции — произведение полусуммы оснований на высоту:

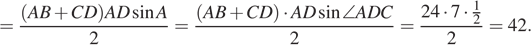
 Ответ: 42.

Задача 2. В прямоугольной трапеции с основаниями и угол прямой, , . Найдите среднюю линию трапеции.

Решение.

Для того, чтобы найти среднюю линию трапеции необходимо знать длину оснований, найдём AD.

Проведём высоту СH к AD.

Найдём АD:

Средняя линия трапеции равна полусумме оснований:

 Ответ: 6,5.

Задача 3. Основания трапеции равны 8 и 16, боковая сторона, равная 6, образует с одним из оснований трапеции угол 150°. Найдите площадь трапеции.

Решение.

Угол в 150° образует боковая сторона и меньшее основание, тогда с большим основанием эта сторона образует угол 30°. Проведем высоту трапеции и рассмотрим прямоугольный треугольник. Из определения синуса острого угла прямоугольного треугольника получаем:

По формуле площади трапеции находим

 Ответ: 36.

Задача 4. Основания равнобедренной трапеции равны 56 и 104, боковая сторона равна 30. Найдите длину диагонали трапеции.

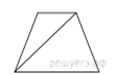
Решение.

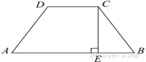
Найдем разницу между двумя основаниями:

Поскольку трапеция равнобедренная, то высотой, проведенной из точки С, а также высотой проведенной из точки D, от нижнего основания "отрезается" 2 равные части. Найдем длину одной из таких частей:

Рассмотрим треугольник СЕВ. Из него (по теореме Пифагора) найдем высоту СЕ:

Рассмотрим, наконец, треугольник АСЕ. В нем мы знаем высоту, а также . Теперь, также по теореме Пифагора найдем искомую диагональ АС, которая является гипотенузой прямоугольного треугольника:

Ответ: 82.

Решить самостоятельно.

1.    Основания равнобедренной трапеции равны 17 и 87. Высота трапеции равна 14. Найдите тангенс острого угла.

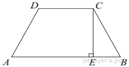
2.    трапеции ABCD известно, что AB = CD, ∠BDA = 54° и ∠BDC = 23°. Найдите угол ABD. Ответ дайте в градусах.

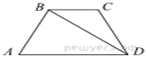
3.    Основания равнобедренной трапеции равны 11 и 21, боковая сторона равна 13. Найдите высоту трапеции.

4.    В прямоугольной трапеции основания равны 4 и 7, а один из углов равен 135°. Найдите меньшую боковую сторону.

Параллелограмм.

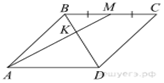
Задача 1. В параллелограмме отмечена точка — середина стороны . Отрезки и пересекаются в точке . Найдите если .

Решение.

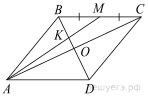
Обозначим О точку пересечения диагоналей параллелограмма. Диагонали параллелограмма точкой пересечения делятся пополам, поэтому ВО — медиана треугольника АВС. Отрезок АМтакже является медианой треугольника АВС, точкой пересечнния медианы делятся в отношении 2 : 1, считая от вершины. Поэтому

 Ответ: 4.

Решить самостоятельно.

5.    В параллелограмме ABCD АВ = 8, АС = ВD =17. Найдите площадь параллелограмма.

6.    В параллелограмме диагональ в два раза больше стороны и . Найдите тупой угол между диагоналями параллелограмма. Ответ дайте в градусах.

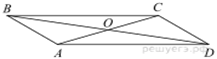
План решения задачи №6.

1)       Рассмотреть  ∆ COD  - равнобедренный с углом при вершине С =104°.

2)       Найти  <COD = <CDO.

3)       Найти величину угла, смежного  с  <COD.

7.    В параллелограмме ABCD диагонали являются биссектрисами его углов, AB = 26, AC = 20. Найдите BD.

8.    Стороны параллелограмма равны 9 и 12. Высота, опущенная на меньшую сторону, равна 8. Найдите высоту, опущенную на большую сторону параллелограмма.

Ромб. Квадрат.Прямоугольник.

Задача 1. Сумма двух углов ромба равна 120°, а его меньшая диагональ равна 25. Найдите периметр ромба.

Решение.

Сумма двух углов ромба равна 120°, значит, каждый угол равен 120° : 2 = 60°. Сумма двух остальных углов ромба равна 360° − 120° = 240°, значит, каждый из них равен 240° : 2 = 120°. Меньшая диагональ ромба лежит напротив меньшего угла ромба 60°, поэтому получаем равносторонний треугольник, основанием которого является данная диагональ. Таким образом, периметр ромба равен 25 · 4 = 100.

Ответ: 100.

Задача 2. Ромб и квадрат имеют одинаковые стороны. Найдите площадь ромба, если его острый угол равен 30°, а площадь квадрата равна 64.

Решение.

Площадь квадрата вычисляется по формуле: . Площадь ромба вычисляется по формуле: Таким образом:

Ответ: 32.     Решить самостоятельно.

9. В ромбе Найдите синус угла .

10.                      Сумма двух углов ромба равна 120°, а его периметр равен 84. Найдите длину меньшей диагонали ромба.

11. Сумма двух углов ромба равна 240°, а его периметр равен 68. Найдите длину меньшей диагонали ромба. 12. Квадрат и прямоугольник имеют одинаковые площади, равные 36 см². Одна из сторон прямоугольника на 2 см меньше стороны квадрата. Найти периметр прямоугольника.

Ответы на задачи.