1

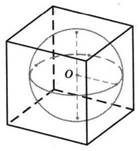Куб описан около сферы радиуса 13,5. Найдите объем куба.

Решение:

Радиус сферы, проведенный в точку касания сферы и плоскости, перпендикулярен к касательной плоскости.

Значит, a = D = 2R = 2 · 13,5 = 27, где a – ребро куба,

                                                                 D – диаметр сферы,                                                                  R – радиус сферы.

V = a³

V = 27³ =19683 Ответ: 129683

Пример 2

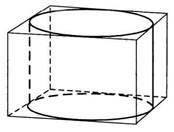Правильная четырехугольная призма описана около цилиндра, радиус основания которого равен 1.

Площадь боковой поверхности призмы равна 8. Найдите высоту цилиндра.

Решение:

По условию призма является правильной. Значит, в ее основании лежит правильный четырехугольник, т.е. квадрат.

R                   = 1 => a = 2R = 2, где a – сторона основания призмы

P_осн. = 4a = 8

S                    8

S_бок. = P_осн. · H                          Отсюда, H1

Pосн. 8 Ответ: 1.

3

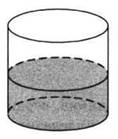В цилиндрический сосуд налили 2900 см³ воды.

Уровень жидкости оказался равным 20 см.

В воду полностью погрузили деталь.

При этом уровень жидкости в сосуде поднялся на 15 см. Чему равен объем детали? Ответ выразите в см³.

Решение:

V S          H

Отсюда, Sосн. V 2900см3 145см2

                                          H        20см

Объем детали равен объему жидкости, вытесненной этой деталью, т.е.

объему цилиндра с основанием 145 см² и высотой 15 см. V_дет. 145 15 2175см³ Ответ: 2175.

Пример 4

В цилиндрическом сосуде уровень жидкости достигает 54 см. На какой высоте будет находиться уровень жидкости, если ее перелить во второй цилиндрический сосуд, диаметр которого в 3 раза больше диаметра первого?

Ответ выразите в сантиметрах.

Решение:

Объем жидкости в обоих сосудах одинаков.

V R²H

По условию диаметр второго сосуда в 3 раза больше диаметра первого, значит, и радиус второго сосуда в 3 раза больше радиуса первого.

R² и H – обратно пропорциональные величины, т.е. при увеличении одной из них в несколько раз другая уменьшится во столько же раз

222                                                                                                               H      54

R2(3R1 )9R16 см

                                                                                9       9

Ответ: 6.

5

Цилиндр и конус имеют общие основание и высоту. Объем конуса равен 60. Найдите объем цилиндра.

Решение:

Vкон.  R2 H                   Vцил. R2 H

Так как по условию цилиндр и конус имеют общие основание и высоту, то Vцил. 3Vкон. 3 60 180

Ответ: 180.

Пример 6

Во сколько раз увеличится объем конуса, если радиус его основания увеличится в 3 раза, а высота останется прежней?

Решение:

Vкон.  R2 H

R² и V_кон. – прямо пропорциональные величины, т.е. при увеличении одной из них в несколько раз другая увеличится во столько же раз

Если радиус основания увеличится в 3 раза, то R² увеличится в 9 раз.

Значит, V_кон. тоже увеличится в 9 раз. Ответ: 9.

Пример 7

Через среднюю линию основания треугольной призмы, объем которой равен 6, проведена плоскость, параллельная боковому ребру. Найдите объем отсеченной треугольной призмы.

Решение:

                                                                                                                                                               =>

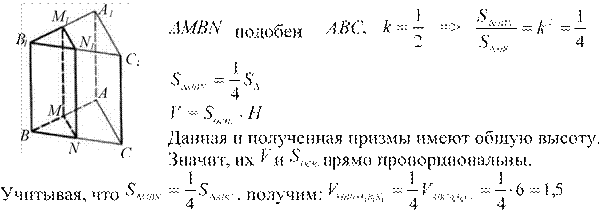ABC

Ответ: 1,5.                                       

8

Найдите объем многогранника, вершинами которого являются точки A, B, C, D, A₁, D₁ параллелепипеда ABCDA₁B₁C₁D₁, у которого AB = 4, AD = 4, AA₁ = 9.

Решение:

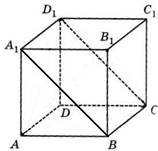AA₁BDD₁C – прямоугольная призма с основанием AA₁B и высотой AD

Vпризм. = Sосн. · H

                                                                    V_AA1BDD₁C S_AA1B AD           AA₁ AB AD

 V_AA1BDD₁C 72

Ответ: 72.

Пример 9

Найдите объем многогранника, вершинами которого являются точки B, C, D, C₁, D₁ параллелепипеда ABCDA₁B₁C₁D₁, у которого AB = 3, AD = 3, AA₁ = 7.

Решение:

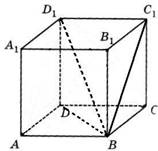
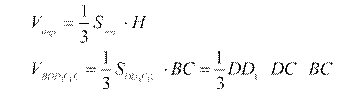
BDD₁C₁C – пирамида с основанием DD₁C₁C и высотой BC

DD₁ = AA₁ = 7, DC = AB =3, BC = AD =3

VBDD1C1C 21

Ответ: 21.

10

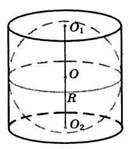Цилиндр, объем которого равен 69, описан около шара. Найдите объем шара.

Решение:

Vцил. R2 H

Учитывая, что H = 2R, получим: V_цил. R² 2R 2 R³

                               3                                     3           2

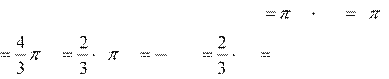Vшара                                                                                  R     2 R    Vцил.          69      46 3

Ответ: 46.

Пример 11

Шар вписан в цилиндр. Площадь поверхности шара равна 132. Найдите площадь полной поверхности цилиндра.

Решение:

Sшара 4 R2

S_{полн.цил.}                    2 R(R H)        2 R(R 2R)      6 R ²            1,5 4 R ²           1,5S_шара          1,5 132      198

Ответ: 198.

Пример 12

В правильной треугольной призме ABCA₁B₁C₁, все ребра которой равны 2, найдите угол между прямыми AA₁ и BC₁. Ответ дайте в градусах.

Решение:

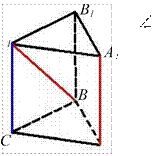(AA₁, BC₁) = (CC₁, BC₁) = CC₁B

^C                                 CC₁B₁B – квадрат, т.к. призма ABCA₁B₁C₁ – правильная

(боковые ребра перпендикулярны к основаниям) и все ее ребра равны 2

Значит, CC₁B = 1/2 CC₁B₁=45° _A   Ответ: 45.

13

В правильной четырехугольной призме ABCDA₁B₁C₁D₁ известно, что D₁B = 2AB. Найдите угол между диагоналями BD₁ и CA₁. Ответ дайте в градусах.

Решение:

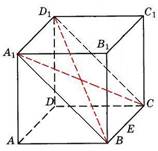Диагонали BD₁ и CA₁ лежат в плоскости прямоугольника A₁BCD₁

В правильной четырехугольной призме диагонали равны и точкой пересечения делятся пополам. Поэтому, A₁O = D₁O = 1/2D₁B = AB = A₁D₁

Таким образом, A₁O = D₁O = A₁D₁, т.е. A₁OD₁ – равносторонний. Отсюда, ( BD₁, CA₁) = A₁OD₁ = 60° Ответ: 60.

Пример 14

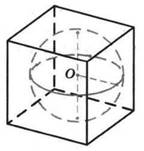Шар, объем которого равен 7, вписан в куб. Найдите объем куба.

Решение:

Vшара   R3

Vкуба (2R)3 42

Ответ: 42.