Подготовка к ЕГЭ математика профильный уровень. Тема "Тема: Функция. Производная. Первообразная"

Задание 7 (базовый уровень, время – 5 мин.)

Тема: Функция. Производная. Первообразная.

Что проверяется:

•      Умение определять значение функции по значению аргумента при различных способах задания функции; описывать по графику

поведение и свойства функции;  

•      Умение вычислять производные и первообразные элементарных функций;

•      Умение исследовать в простейших случаях функции на монотонность;  

Что нужно знать и уметь:

•      Уметь устанавливать связь между характером монотонности функции и знаком ее производной. Если функция возрастает на промежутке и имеет на нем производную, то производная неотрицательна; если функция убывает на промежутке и имеет на нем производную, то производная неположительна.

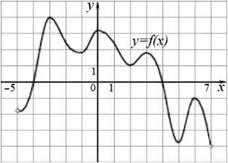Функция (см. рис.) возрастает на промежутках х∈(−5;−3)∪(−1;0)∪(2;3)∪(5;6), следовательно, на этих же промежутках производная функции положительна. На

промежутках х∈(−3;−1)∪(0;1)∪(3;5)∪(6;7)

 функция убывает, значит, на этих промежутках производная функции отрицательна.

•      Уметь с помощью графика функции решать уравнения вида f ′( )x = 0 Теорема: Если функция у = f ( )x имеет экстремум в точкех = х₀, то в этой точке производная функции либо равна нулю, либо не существует 

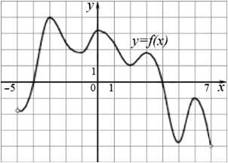На интервале (-5; 7) функция имеет семь экстремумов. Следовательно, уравнение f ′( )x = 0имеет семь решений.

•      Уметь по знаку производной устанавливать характер монотонности функции. 

Если во всех точках открытого промежутка Х выполняется неравенство  ^{f ′( )x ≥ 0} (причем равенство ^{f ′( )x = 0} либо не выполняется, либо выполняется в конечном множестве точек), то функция  ^{y=f(x)возрастает} на промежутке Х.  

Если во всех точках открытого промежутка Х выполняется неравенство ^{f ′( )x ≤ 0} (причем равенство ^{f ′( )x = 0} либо не выполняется, либо выполняется в конечном множестве точек), то функция  ^{y=f(x)убывает} на промежутке Х.

•      Понимать физический смысл производной. Уметь находить скорость для процесса, заданного формулой или графиком.

s = s t( ) - закон движения, где t – время (в секундах), s(t) – положение тела на прямой (координата движущейся материальной точки) в момент времени t по отношению к началу отсчета.  

v = s t′( )

• Понимать геометрический смысл производной

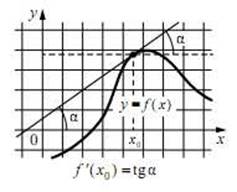
f ′(x₀) = tgα, где α – угол между касательной и положительным

направлением оси х.

• Уметь составлять уравнение прямой по двум точкам. Составить уравнение прямой, проходящую через 2 точки (х₁; у₁)и (х₂; у₂)

kх₁ + b = y

1    способ: Составим систему:          ¹

kx₂ +b = y₂

Решив систему, найдем k и b. Таким образом, составим уравнение прямой.

                                                                                                            х−х¹                у−у¹

2    способ: Воспользоваться формулой = - уравнение прямой по х2 −х1 у2 −у1

двум точкам

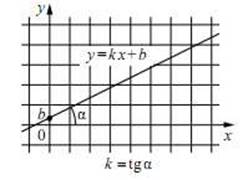•    Знать при каком условии прямые параллельны.

Две прямые параллельны тогда и только тогда, когда равны их угловые коэффициенты.

•    Умение составлять уравнение касательной к графику функции y = f ′(x0)(x − x0) + f (x0) - уравнение касательной 

•    Умение находить площадь криволинейной трапеции.  

b

S = ∫ f ( )x dx = F( )b − F( )a , где F(x) – первообразная для f(x)

a