Целью лабораторной работы является изучение возможностей средства Поиск решения MS Excel для решения оптимизационных задач.

К защите лабораторной работы студент должен предоставить файл ЛР3_ФамилияИО.xlsx с решенными задачами на листах: Задача1, Задача2, Задача3, Задача4.

 

Сохраните рабочую книгу MS Excel в своей папке под именем ЛР3_ФамилияИО.xlsx.

 

Задача 1. Транспортная задача
	Постановка задачи

Некоторая фирма имеет 4 фабрики и пять центров распределения товаров. Фабрики располагаются в Витебске, Гомеле, Могилеве и Полоцке и имеют производственные мощности для выпуска соответственно 200, 150, 225 и 175 единиц продукции ежедневно. Центры распределения товаров располагаются в Минске, Бресте, Пинске, Гродно и Лиде и имеют ежедневные потребности в продукции 100, 200, 50, 250 и 150 единиц соответственно. Стоимость перевозки единицы продукции с фабрик в пункты распределения приведена в таблице 1.

Таблица 1 – Транспортные расходы

Стоимость перевозок

                                         Фабрики          Склады

                                                                                             Минск      Брест      Пинск     Гродно      Лида

                                        Витебск                              $2,00      $2,00      $1,75      $2,25      $2,25

                                        Гомель                               $2,50      $0,50      $1,50      $1,00      $1,50

                                        Могилев                              $1,50      $1,50      $1,75      $1,75      $1,75

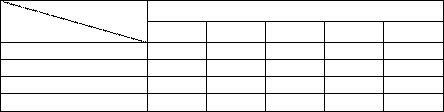                                         Полоцк                               $2,00      $2,00      $1,75      $1,75      $1,75

Необходимо так спланировать перевозки, чтобы минимизировать суммарные транспортные расходы.

Оценка информации. Данная модель сбалансирована, т.е. суммарный объем произведенной продукции (750) равен суммарному объему потребностей в ней (750).

Введем обозначения:

•       x_ij – объем перевозок с i-й фабрики в j-й центр распределения;

•       c_ij – стоимость перевозки единицы продукции с i-й фабрики в j-й центр распределения;         a_i – объем производства на i-й фабрике;

•       b_j – спрос в j-м центре распределения.

Математическая модель этой задачи состоит из трех ограничений:

               4                                                              5

 x_ij  b_j, j 1,5;            x_ij  a_i,  i 1,4;           x_ij  0,  i 1,4, j 1,5

              i1                                                                  j1

4 5

и целевой функции, минимизирующей транспортные расходы: c_ij x_ij  min .

i 1 j 1

 

Порядок выполнения:

Переименуйте Лист1 рабочей книги, новое имя листа – Задача1. Сохраните файл. Выполните следующую подготовительную работу для решения транспортной задачи с помощью средства Поиск решения (рисунок 1).

 

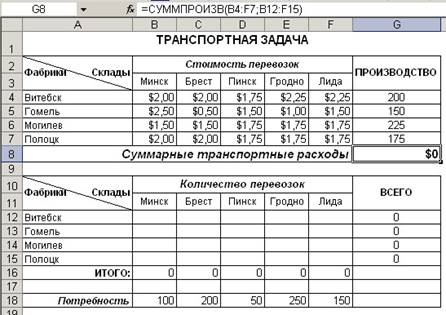
Рисунок 1 – Исходные данные транспортной задачи

В ячейки диапазона G12:G15 введите формулы, вычисляющие суммарный объем товаров по каждой фабрике,  а в ячейки B16:F16 – формулы, вычисляющие объемы доставляемой продукции в пункты распределения. В целевую ячейку G8 введите формулу, вычисляющую суммарные транспортные расходы.

При создании вычислительной модели используем инструмент Поиск решения и заполняем диалоговое окно, как показано на рисунке 2. Нажмите кнопку Параметры диалогового окна Поиск решения. Откроется диалоговое окно Параметры поиска решения, в котором необходимо установить Линейность модели (рисунок 3).

После нажатия кнопки Найти решение будут найдены оптимальный план поставок продукции и соответствующие ему транспортные расходы (рисунок 4). Сохраните найденное решение.

 

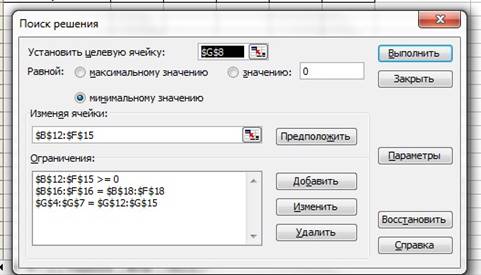
Рисунок 2 – Окно Поиск решения после заполнения для транспортной задачи

 

 

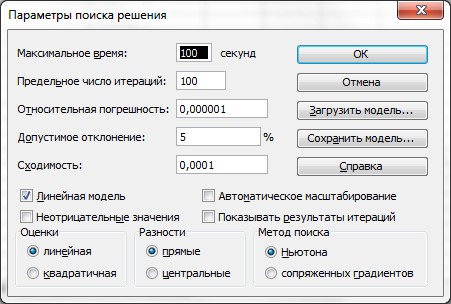
Рисунок 3 – Окно Параметры поиска решения после заполнения для транспортной задачи

 

 

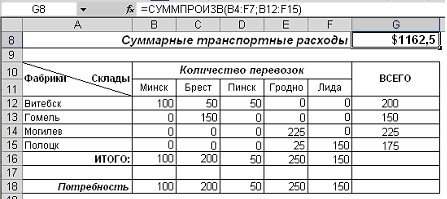
Рисунок 4 – Решенная транспортная задача

Задача 2. О планировании производства
	Постановка задачи

Предприятие электронной промышленности выпускает две модели радиоприемников, причем каждая модель производится на отдельной технической линии. Суточный объем производства первой линии – 60 изделий, второй линии – 75 изделий. На радиоприемник первой модели расходуется 10 однотипных элементов электронных схем, на радиоприемник второй модели – 8 таких элементов. Максимальный суточный запас используемых элементов равен 800 единицам. Прибыль от реализации одного радиоприемника первой и второй модели равна 30 и 20 у.е. соответственно. Определите оптимальный суточный объем производства первой и второй моделей.

Оценка информации. Предприятию необходимо спланировать объем выпуска радиоприемников так, чтобы максимизировать прибыль.

Введем обозначения:

•       x₁ – суточный объем выпуска радиоприемников первой модели;

•       x₂ – суточный объем выпуска радиоприемников второй модели.

Математическая модель этой задачи состоит из ограничений:

              x₁ 60                                                 

                                                        x _j  0,  j 1,2

              x₂ 75                                                          

^10x₁ 8x₂ 800

Кроме того, на ^x₁ и ^x₂ налагаются условия целочисленности, т.е. полученные в результате расчетов значения объемов выпуска должны быть целыми числами.

Целевая функция 30x₁ 20x₂ max .

Порядок выполнения:

Выполните следующую подготовительную работу для решения задачи о планировании производства с помощью средства Поиск решения (рисунок 5).

 

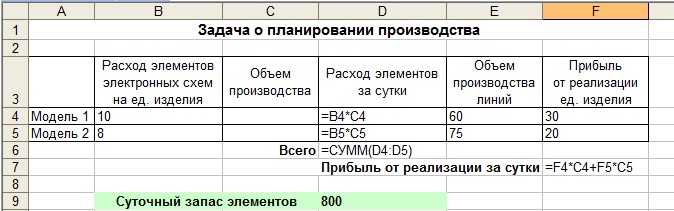
Рисунок  5 - Таблица с исходными данными и формулами

Введите в ячейки С4 и С5 данные об объемах выпуска радиоприемников, удовлетворяющие условиям задачи (допустимый план задачи), равные 40 единицам. Просмотрите полученные результаты.

При создании вычислительной модели используем инструмент Поиск решения и заполняем диалоговое окно, как показано на рисунке 6.

 

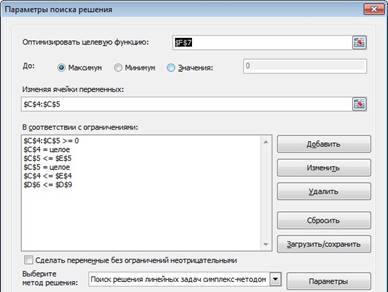
Рисунок 6 - Окно Поиск решения для задачи о планировании производства

После нажатия кнопки Найти решение будут найдены оптимальный план производства. Проанализируйте изменения в таблице.

Переименуйте Лист2 с решенной задачей, новое имя листа – Задача2. Сохраните файл. (Впоследствии каждую задачу необходимо решать на новом листе рабочей книги, листы называть соответственно задачам).

 

Задача 3. О снабжении
	Постановка задачи

Некоторое учреждение приняло решение одеть своих сотрудников в фирменные костюмы. Оно получило предложения от фирм f1, f2 и f3 на поставку фирменных костюмов трех размеров: s1, s2 и s3. Стоимость костюмов приведена в таблице 2.

Таблица 2 – Стоимость костюмов

	s1	s2	s3
фирма f1	110	115	126
фирма f2	107	115	130
фирма f3	104	109	116

Будут заключены контракты на покупку 1000 костюмов размера s1, 1500 костюмов размера s2 и 1200 костюмов размера s3. Производственные мощности фирм позволяют выпускать 1000 костюмов разных размеров фирме f1, 1500 костюмов фирме f2 и 2500 костюмов фирме f3.

Как следует распределить заказы, чтобы контракты были заключены с минимизацией общей стоимости?

Оценка информации. Заметим, что общее предложение (5000) превосходит общий спрос (3700), т.е. налицо некоторая избыточная производственная мощность. Мы понимаем, что учреждение должно получить ровно столько костюмов, сколько работников оно собирается ими обеспечить. А вот с какой фирмы и сколько будет взято костюмов, выяснится в результате решения задачи. Введем обозначения:

•              a1, a2, a3 – количество костюмов размера s1, выпускаемых соответственно фирмами f1, f2 и f3;

•              b1, b2, b3 – количество костюмов размера s2, выпускаемых соответственно фирмами f1, f2 и f3;  c1, c2, c3 – количество костюмов размера s3, выпускаемых соответственно фирмами f1, f2 и f3. Математическая модель этой задачи состоит из шести ограничений:

a1 + a2 + a3 = 1000, b1 + b2 + b3 = 1500, c1 + c2 + c3 = 1200, a1 + b1 + c1 <= 1000, a2 + b2 + c2 <= 1500, a3 + b3 + c3 <= 2500

и целевой функции, минимизирующей общую стоимость:

110a1 + 107a2 + 104a3 + 115b1 + 115b2 + 109b3 + 126c1 + 130c2 + 116c3 → min.

Порядок выполнения:

Выполните следующую подготовительную работу для решения задачи (рисунок 7).

 

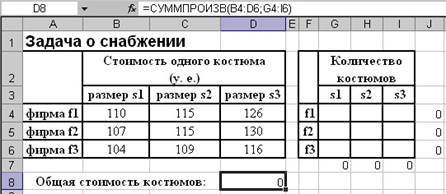
Рисунок 7 – Исходные данные для задачи о снабжении

В ячейки J4:J6 введите формулы для расчета общего объема поставок от фирм f1, f2 и f3 соответственно, используя функцию СУММ. В ячейки G7:I7 введите формулы, подсчитывающие общее количество костюмов s1, s2 и s3. В целевой ячейке D8 подсчитайте общую стоимость костюмов.

При создании вычислительной модели используем инструмент Поиск решения, т.к. задача имеет достаточно много переменных (9). При этом для изменяемых ячеек (переменных) необходимо будет добавить два ограничения. Значения их должны быть целочисленными и неотрицательными (рисунок 8). Всего должно быть 8 ограничений.

 

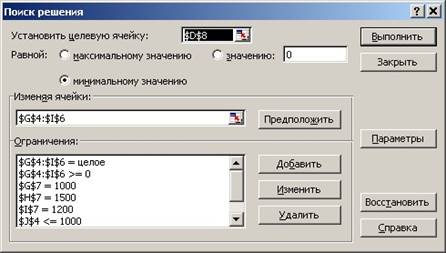
Рисунок 8 – Окно Поиск решения после заполнения для задачи о снабжении

После нажатия кнопки Найти решение получим оптимальный план распределения заказов (рисунок 9). Сохраните файл.

 

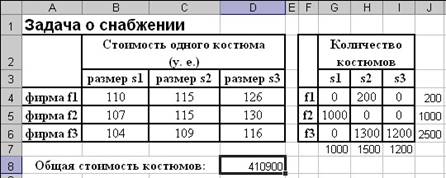
Рисунок 9 – Решенная задача о снабжении

 

Задача 4. О назначениях
	Постановка задачи

Имеются четыре рабочих и четыре вида работ. Стоимости c_ij выполнения i-м рабочим j-й работы приведены  в таблице 3, где под строкой понимается рабочий, а под столбцом – работа

Таблица 3 – Стоимость выполнения работ

1	4	6	3
9	10	7	9
4	5	11	7
8	7	8	5

Рабочие

 

 

 

                                                                                                                             Виды работ

Необходимо составить план выполнения работ так, чтобы все работы оказались выполненными, каждый рабочий был загружен только на одной работе, а суммарная стоимость выполнения всех работ была минимальной.

Оценка информации. Данная задача является сбалансированной, т.е. число работ совпадает с числом рабочих. Если задача не сбалансирована, то перед началом решения ее необходимо сбалансировать, введя недостающее число фиктивных строчек или столбцов с достаточно большими штрафными стоимостями работ. Введем обозначения:

•       x_ij – переменная, имеющая только два допустимых значения: 0 или 1 (такие переменные называются двоичными);        x_ij=1, если i-м рабочим выполняется j-я работа;

•       x_ij=0, если i-м рабочим не выполняется j-я работа.

Математическая модель этой задачи состоит из ограничений: 

                4                                                                                                 4                                                                                                  

 xij 1, j 1,4; i1

xij 1,  i 1,4; j1

xij {0,1},i 1,4, j 1,4

                                                                                                                                                                        4       4

и целевой функции, минимизирующей суммарную стоимость выполнения всех работ: c_ij x_ij  min .

i 1 j 1 Порядок выполнения:

Выполните следующую подготовительную работу для решения задачи о назначениях с помощью средства Поиск решения (рисунок 10).

 

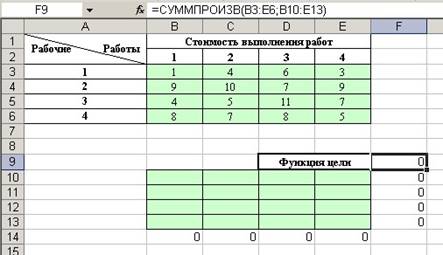
Рисунок 10 – Исходные данные задачи о назначениях

В ячейки диапазона B14:E14 и F10:F13 введите следующие формулы, задающие левые части ограничений:

Ячейка	Формула	Ячейка	Формула
B14	=СУММ(B10:B13)	F10	=СУММ(B10:E10)
C14	=СУММ(C10:C13)	F11	=СУММ(B11:E11)
D14	=СУММ(D10:D13)	F12	=СУММ(B12:E12)
E14	=СУММ(E10:E13)	F13	=СУММ(B13:E13)

В целевую ячейку F9 введите формулу, вычисляющую суммарную стоимость выполнения работ.

При создании вычислительной модели используем инструмент Поиск решения и заполняем диалоговое окно, как показано на рисунке 11.

 

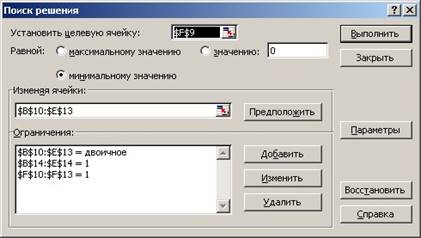
Рисунок 11 – Окно Поиск решения после заполнения для задачи о назначениях

После нажатия кнопки Найти решение получим оптимальный план выполнения работ. Сохраните файл.

 

ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
Задача 5. Транспортная задача
	Постановка задачи

Имеются n пунктов производства и m пунктов распределения продукции. Стоимость перевозки единицы продукции с i-го пункта производства в j-й центр распределения c_ij приведена в таблице, где под строкой понимается пункт производства, а под столбцом – пункт распределения. Кроме того, в этой таблице в i-й строке указан объем производства  в i-м пункте производства, а в j-м столбце указан спрос в j-м центре распределения. Необходимо составить план перевозок продукции в пункты распределения, минимизирующий суммарные транспортные расходы.

 

Задача 6. Транспортная задача
	Постановка задачи

На складах w1, w2, w3 хранятся соответственно 15, 25, 20 кроватей, которые должны быть распределены по четырем магазинам ml, m2, mЗ, m4, где требуется 20, 12, 5 и 9 кроватей. Пусть стоимость перевозки одной кровати со склада  в магазин задается следующей таблицей в условных единицах:

Склад	Магазин
	ml	m2	m3	m4
w1	2	2	2	4
w2	3	1	1	3
w3	3	6	3	4

Как следует планировать перевозку для минимизации стоимости?

 

 

Задача 7. Транспортная задача
	Постановка задачи

Компания владеет тремя заводами А, В, С. Объем их производства равен соответственно 6000, 3000 и 3000 единиц. Компания обязалась поставлять соответственно 1500, 2500, 2700 и 3300 единиц продукции в города W, X, Y, Z. При заданных стоимостях перевозок составьте оптимальный план распределения.

 

 

Задача 8. Задача о назначениях
	Постановка задачи

Имеются n рабочих мест и m видов работ. Стоимость c_ij выполнения i-м рабочим j-й работы приведена в таблице, где под строкой понимается рабочий, а под столбцом – работа. Необходимо составить план работ так, чтобы все работы были выполнены, каждый рабочий был занят только на одной работе, а суммарная стоимость работ была минимальной.

Вариант 1.

	Стоимость выполнения работ
3	6	2	5
1	2	7	11
5	12	11	9
2	4	2	10

 

Рабочие

 

 

 

                                                                                                       Виды работ

 

Вариант 2.

	Стоимость выполнения работ
1	3	6	5
5	2	7	8
3	5	1	9
6	4	2	10

 

Рабочие

 

 

 

                                                                                                       Виды работ

 

 

Задача 9. Производственная задача
	Постановка задачи

Фирма производит две модели А и В сборных книжных полок. Их производство ограничено наличием сырья (высококачественных досок) и временем машинной обработки. Для каждого изделия модели А требуется 3м² досок, а для изделия модели В – 4м². Фирма может получать до 1700м² досок в неделю. Для каждого изделия модели А требуется 12 минут машинного времени, а для изделия модели В – 30 минут. В неделю можно использовать 160 часов машинного времени.

Сколько изделий каждой модели следует фирме выпускать в неделю, чтобы получить максимальную прибыль, если каждое изделие модели А приносит 2 условные единицы прибыли, а каждое изделие модели В – 4 условные единицы прибыли?

 

 

Задача 10. Производственная задача
	Постановка задачи

Фирма производит два продукта А и В, рынок сбыта которых неограничен. Каждый продукт должен быть обработан каждой из машин I, II, III. Время обработки в часах для каждого из продуктов А и В приведено в таблице. Время работы машин I, II, III соответственно равно 40, 36 и 36 часов в неделю. Прибыль от изделий А и В составляет соответственно 5 и 5 условных единиц. Фирме надо определить недельные нормы выпуска продуктов А и В, максимизирующие прибыль.

		Машины
	I	II	III
продукт А продукт В	0,5 0,25	0,4 0,3	0,2 0,4

 

 

Задача 11. Производственная задача
	Постановка задачи

Процесс изготовления изделий двух видов А и В некоторым заводом требует, во-первых, последовательной обработки на токарных и фрезерных станках, во-вторых, затрат двух видов сырья: стали и цветных металлов. В таблице приводятся данные о потребности каждого ресурса на единицу выпускаемого изделия, общие запасы ресурсов и прибыль от реализации каждой единицы изделия. Определить такой план выпуска продукции, который обеспечивает максимальную прибыль при условии, что время работы фрезерных станков должно быть использовано полностью.

 

 

Задача 12. Производственная задача
	Постановка задачи

Производитель безалкогольных напитков располагает двумя разливочными машинами А и В. Машина А спроектирована для пол-литровых бутылок, а машина В - для литровых, но каждая из них может использоваться для обоих типов бутылок с некоторой потерей эффективности в соответствии с приведенными в таблице сведениями о работе машин, каждая из машин работает ежедневно по 6 часов при пятидневной рабочей неделе. Прибыль от поллитровой бутылки составляет 4 цента, а от литровой - 10 центов. Недельная продукция не может превосходить 50000 л; рынок принимает не более 44000 пол-литровых бутылок и 30000 литровых. Требуется максимизировать прибыль.

Машина	Количество бутылок, производимых в 1 мин.
	пол-литровые	литровые
А В	50 40	20 30