Добавить материал

и получить 10 документов
и свидетельство СМИ

Шкода Лидия Ильинична

Показательные уравнения из материалов ЕГЭ профильного уровня.

Домашняя работа
docx
04.01.2023

Публикация в СМИ для учителей

Бесплатное участие. Свидетельство СМИ сразу.
Мгновенные 10 документов в портфолио.

Добавить материал

Подробно разобраны решения 7 примеров и даны 4 примера для с. р.

Показ.ур.проф.из ЕГЭ.docx

Показательные уравнения из материалов ЕГЭ профильного уровня.

1. а)  Решите уравнение

б)  Найдите все корни этого уравнения, принадлежащие промежутку

Решение. а)  Заметим, что преобразуем исходное уравнение:

Пусть тогда уравнение запишется в виде откуда или

При получим: откуда

б)  Корень не принадлежит промежутку Поскольку и корень принадлежит промежутку

Ответ: а) б)

2. а)  Решите уравнение

б)  Укажите корни этого уравнения, принадлежащие отрезку

Решение. а)  Разложим левую часть на множители:

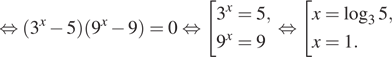
равносильно левая круглая скобка 3 в степени x минус 5 правая круглая скобка левая круглая скобка 9 в степени x минус 9 правая круглая скобка =0 равносильно совокупность выражений 3 в степени x =5,9 в степени x =9 конец совокупности . равносильно совокупность выражений x= логарифм по основанию 3 5,x=1. конец совокупности .

б)  Поскольку отрезку принадлежит только корень

Ответ: а) б)

Примечание.

Можно было ввести замену получить уравнение и решить его разложением на множители:

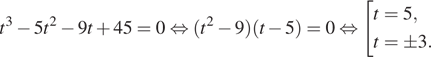
$t в кубе минус 5t в квадрате минус 9t плюс 45=0 равносильно левая круглая скобка t в квадрате минус 9 правая круглая скобка левая круглая скобка t минус 5 правая круглая скобка =0 равносильно совокупность выражений t=5,t=\pm3. конец совокупности .$

Возвращаясь к исходной переменной получаем решение.

3. а)  Решите уравнение

б)  Укажите корни этого уравнения, принадлежащего отрезку

Решение. а)  Преобразуем исходное уравнение:

Пусть тогда уравнение запишется в виде откуда или

При получим: откуда

б)  Поскольку 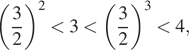левая круглая скобка дробь: числитель: 3, знаменатель: 2 конец дроби правая круглая скобка в квадрате меньше 3 меньше левая круглая скобка дробь: числитель: 3, знаменатель: 2 конец дроби правая круглая скобка в кубе меньше 4, получаем: Значит, отрезку принадлежит число

Ответ: а) б)

Критерии проверки:

Ответ: а) б)

514081

а) б)

Методы алгебры: Замена переменной

4. а)  Решите уравнение

б)  Найдите все корни этого уравнения, принадлежащие отрезку [−1; 2].

Решение. а)  Преобразуем уравнение:

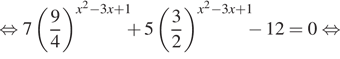
$равносильно 7 левая круглая скобка дробь: числитель: 9, знаменатель: 4 конец дроби правая круглая скобка в степени левая круглая скобка x в квадрате минус 3x плюс 1 правая круглая скобка \!\!\!\! плюс 5 левая круглая скобка дробь: числитель: 3, знаменатель: 2 конец дроби правая круглая скобка в степени левая круглая скобка x в квадрате минус 3x плюс 1 правая круглая скобка \!\!\!\! минус 12 = 0 равносильно$
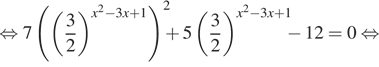
$равносильно 7 левая круглая скобка левая круглая скобка дробь: числитель: 3, знаменатель: 2 конец дроби правая круглая скобка в степени левая круглая скобка x в квадрате минус 3x плюс 1 правая круглая скобка правая круглая скобка в квадрате \!\!\!\! плюс 5 левая круглая скобка дробь: числитель: 3, знаменатель: 2 конец дроби правая круглая скобка в степени левая круглая скобка x в квадрате минус 3x плюс 1 правая круглая скобка \!\!\!\! минус 12 = 0 равносильно$
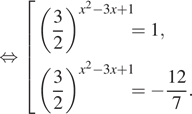
$равносильно совокупность выражений левая круглая скобка дробь: числитель: 3, знаменатель: 2 конец дроби правая круглая скобка в степени левая круглая скобка x в квадрате минус 3x плюс 1 правая круглая скобка \!\!\!\!=1, левая круглая скобка дробь: числитель: 3, знаменатель: 2 конец дроби правая круглая скобка в степени левая круглая скобка x в квадрате минус 3x плюс 1 правая круглая скобка \!\!\!\!= минус дробь: числитель: 12, знаменатель: 7 конец дроби . конец совокупности$

У второго уравнения решений нет.

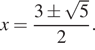
Преобразуем первое уравнение: откуда $x= дробь: числитель: 3 \pm корень из 5, знаменатель: 2 конец дроби .$

б)  Оценим целыми числами: Тогда

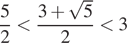дробь: числитель: 5, знаменатель: 2 конец дроби меньше дробь: числитель: 3 плюс корень из 5, знаменатель: 2 конец дроби меньше 3 и 0 меньше дробь: числитель: 3 минус корень из 5, знаменатель: 2 конец дроби меньше дробь: числитель: 1, знаменатель: 2 конец дроби .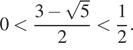

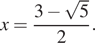
Значит, отрезку принадлежит только x= дробь: числитель: 3 минус корень из 5, знаменатель: 2 конец дроби .

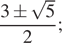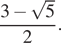
Ответ: а) $дробь: числитель: 3 \pm корень из 5, знаменатель: конец дроби 2;$ б) дробь: числитель: 3 минус корень из 5, знаменатель: 2 конец дроби .

Критерии проверки:

Методы алгебры: Замена переменной,

5. а)  Решите уравнение

б)  Укажите корни этого уравнения, принадлежащие отрезку

Решение. a)  Сделаем замену переменной: тогда

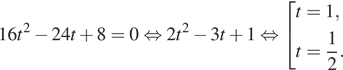
16t в квадрате минус 24t плюс 8=0 равносильно 2t в квадрате минус 3t плюс 1 равносильно совокупность выражений t=1, t= дробь: числитель: 1, знаменатель: 2 конец дроби . конец совокупности .

Вернёмся к исходной переменной:

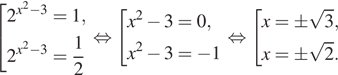
$совокупность выражений 2 в степени левая круглая скобка x в квадрате минус 3 правая круглая скобка =1, 2 в степени левая круглая скобка x в квадрате минус 3 правая круглая скобка = дробь: числитель: 1, знаменатель: 2 конец дроби конец совокупности . равносильно совокупность выражений x в квадрате минус 3=0, x в квадрате минус 3= минус 1 конец совокупности . равносильно совокупность выражений x=\pm корень из 3, x=\pm корень из 2. конец совокупности .$

б)  Заметим, что при этом Поэтому в заданном отрезке лежат корни $\pm корень из 2, корень из 3.$

Ответ: а) б)

6. а)  Решите уравнение

б)  Укажите корни этого уравнения, принадлежащие промежутку

Решение. а)  Разделим обе части уравнения на положительное выражение и решим квадратное уравнение:

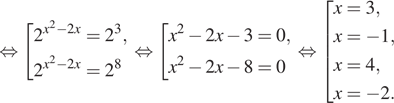
б)  Заметим, что и поэтому на заданном промежутке лежат корни x = 3 и x = 4.

Ответ:a) {−2; −1; 3; 4}, б) {3; 4}.

7. а)  Решите уравнение

б)  Найдите все корни этого уравнения, принадлежащие отрезку [−0,5; 0,5].

Решение. а)  Последовательно получаем:

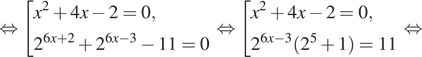
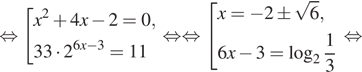
$равносильно совокупность выражений x в квадрате плюс 4x минус 2 = 0,33 умножить на 2 в степени левая круглая скобка 6x минус 3 правая круглая скобка = 11 конец совокупности . равносильно равносильно совокупность выражений x = минус 2 \pm корень из 6,6x минус 3 = логарифм по основанию целая часть: 2, дробная часть: числитель: 1, знаменатель: 3 конец совокупности . равносильно$
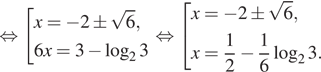
$равносильно совокупность выражений x = минус 2 \pm корень из 6,6x = 3 минус логарифм по основанию 2 3 конец совокупности . равносильно совокупность выражений x = минус 2 \pm корень из 6,x = дробь: числитель: 1, знаменатель: 2 конец дроби минус дробь: числитель: 1, знаменатель: 6 конец дроби логарифм по основанию 2 3. конец совокупности .$

б)  Найдем корни на отрезке Так как этот корень не будет принадлежать отрезку Проверим другие значения x. Заметим, что

$9 меньше 24 меньше 25 \Rightarrow 3 меньше 2 корень из 6 меньше 5 \Rightarrow$
$\Rightarrow дробь: числитель: 3, знаменатель: 2 конец дроби меньше корень из 6 меньше дробь: числитель: 5, знаменатель: 2 конец дроби \Rightarrow минус дробь: числитель: 1, знаменатель: 2 конец дроби меньше корень из 6 минус 2 меньше дробь: числитель: 1, знаменатель: 2 конец дроби .$

Значит, корень принадлежит отрезку [−0,5; 0,5]. Наконец,

$1 меньше 3 меньше 64 \Rightarrow 0 меньше логарифм по основанию 2 3 меньше 6 \Rightarrow$
$\Rightarrow минус 1 меньше минус дробь: числитель: 1, знаменатель: 6 конец дроби логарифм по основанию 2 3 меньше 0 \Rightarrow минус дробь: числитель: 1, знаменатель: 2 конец дроби меньше дробь: числитель: 1, знаменатель: 2 конец дроби минус дробь: числитель: 1, знаменатель: 6 конец дроби логарифм по основанию 2 3 меньше дробь: числитель: 1, знаменатель: 2 конец дроби .$

Значит, корень принадлежит отрезку [−0,5; 0,5].

Ответ: а) б)

Решить самостоятельно.

1. а)  Решите уравнение:

б)  Определите, какие из его корней принадлежат отрезку

2. а)  Решите уравнение

б)  Найдите все корни этого уравнения, принадлежащие отрезку

3. а)  Решите уравнение

б)  Найдите все корни этого уравнения, принадлежащие отрезку [−0,5; 0,5].

4.а)Решитеуравнение.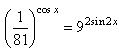
б) Укажите корни этого уравнения, принадлежащие отрезку .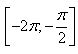

Скачано с www.znanio.ru

Возвращаясь к исходной переменной получаем решение

Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.

Посмотрите также