1. ПОСТРОЕНИЕ СЕТЕВЫХ ГРАФИКОВ

 

Задача планирования и управления комплексом взаимосвязанных работ возникает всякий раз при реализации сложных проектов /1, 2, 3/. Работы взаимосвязаны в том смысле, что выполнение последующих работ может быть начато только после завершения предшествующих, т. е. ряд работ выполняется параллельно, а ряд – только последовательно. Наиболее наглядный пример таких работ – строительство: укладке фундамента предшествует установка строительных механизмов и доставка материалов, которые, в свою очередь, могут выполняться одновременно; затем последовательно возводятся стены, кровля, после чего начинаются внутренние работы; сантехнические и электромонтажные работы, как правило, тоже могут выполняться параллельно, а уже потом выполняется отделка, облицовка и т.д.

Решение задачи планирования и управления такими комплексами может осуществляться на основе опыта и интуиции руководителя работ. Однако, если проект включает выполнение сотен и более работ, интуитивный подход не обеспечивает нахождения оптимальных решений. В этом случае требуется использовать математические модели и методы, а именно методы сетевого планирования /1, 2, 3/.

Впервые методы сетевого планирования и управления начали применять в 50-х годах независимо в СССР и в США при реализации ядерных и ракетно-космических проектов. Их эффективность оказалась столь высока, что они очень быстро нашли широкое применение в различных отраслях народного хозяйства: в строительстве, в промышленности, на транспорте, при организации научных исследований и т.д.

Методы сетевого планирования позволяют решать задачи анализа и синтеза сетевых графиков, т.е. оценки существующих планов и составления оптимальных (наилучших) планов по тем или иным показателям, с учетом ограничений по времени, необходимого для выполнение всего комплекса работ и отдельных его составляющих, а также по материальным, энергетическим, трудовым ресурсам в натуральном или стоимостном выражении. В результате решения задачи должен быть получен подробный план с расшифровкой, когда какие работы должны начинаться и завершаться выполнением, когда, в какое время и какие ресурсы могут потребоваться и как во времени они будут расходоваться, что произойдет при нарушении графика выполнения той или иной работы и т.п.

Исходными данными для задачи планирования и управления проектом является перечень работ, входящих в состав проекта, и последовательность их выполнения. Обычно работы сводят в структурную таблицу, где их принято обозначать буквами а₁, а₂ …а_i. Если работа  может быть начата только после завершении работ , то говорят, что она опирается на эти работы: .

Решение задачи осуществляется методом сетевого планирования, где рассматриваемый проект представляется в виде сетевого графика (направленного графа, рис. 1). Достоинство математической модели в виде сетевого графика состоит в наглядности, что упрощает ее анализ при планировании и управлении выполнением комплекса работ.

Рассмотрим пример, приведенный в таблице 1. Прочерк в колонке 2 табл. 1 означает, что работа не опирается ни на какие другие работы и ее выполнение может быть начато немедленно в момент начала выполнения проекта.

 

Таблица 1

 

Составление сетевого графика начинают с упорядочения работ в последовательности их выполнения, для чего их подразделяют на ранги. К первому рангу относят работы, которые не опираются ни на какие другие работы. Работы второго ранга опираются только на работы первого ранга; работы к-го ранга опираются хотя бы на одну работу (к-1)-го ранга и могут опираться на работы более низких рангов.

При построении сетевого графика необходимо соблюдать следующие правила:

– каждая работа в сети проекта представляется одной и только одной дугой;

– для правильного выполнения проекта необходимо соблюдать отношения предшествования для работ проекта;

– каждый процесс идентифицируется двумя концевыми узлами (событиями); для параллельный работ необходимо, чтобы хотя бы один концевой узел был уникальным (рис. 2, а).

 

Рис. 2, б

Рис. 2, а

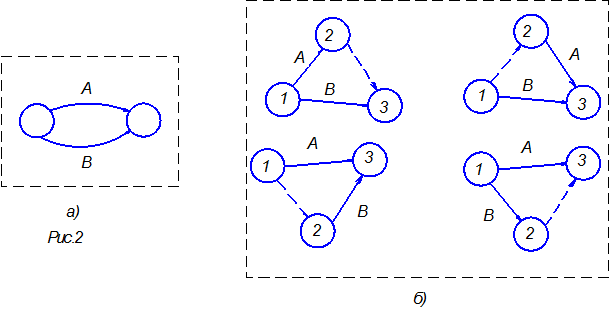
В случае если последнее правило автоматически не выполняется для параллельных процессов (рис. 2, а) в сетевой график вводят фиктивные работы одним из четырех способов (рис. 2, б), которые на графике изображаются пунктирной линией и не поглощают временных и других ресурсов. Таким образом, параллельные работы имеют хотя бы один уникальный концевой узел.

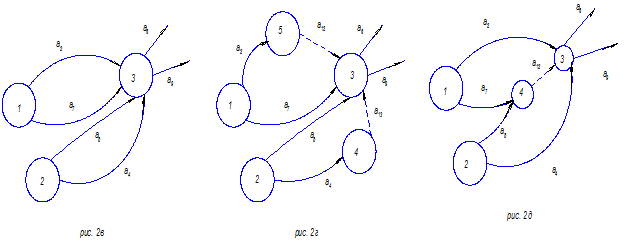
В исходных данных (табл. 1) рассматриваемого примера работа  отсутствует. Внимательно рассмотрев табл. 1, можно увидеть, что работы  опираются на работы (т.е. имеют один общий концевой узел, рис. 2, в), при этом работы  и работы  имеют попарно другой общий концевой узел, т.е. имеем две пары параллельных процессов:  и . Для правильного их указания в сети необходимо ввести фиктивные работы. Это можно сделать двумя путями: ввести фиктивную работу для каждой пары (рис. 2, г) или ввести только одну фиктивную работу, объединив работы из разных групп, например: введем фиктивную работу , для выполнения которой не требуется никаких затрат времени и ресурсов, (поэтому на сетевом графике ее принято изображать пунктирной стрелкой (рис. 2, д), опирающейся на работы .

В колонке 3 табл. 1 приведены ранги всех работ, включая фиктивную работу . После упорядочения работ по рангам, им присваиваются новые номера таким образом, чтобы работы более низких рангов имели меньшие порядковые номера. Внутри одного ранга работы нумеруются произвольно. Новые обозначения работ, помеченные звездочкой, приведены в колонке 4. Структурная таблица в новых обозначениях (для простаты записи звездочки опущены) приведена в табл. 2.

Рис. 2, в                          Рис. 2, г                         Рис. 2, д

 

Таблица 2

 

Новые обозначения работ	Опираются на работы	Ранг
1	2	3
а1	–	1
а2	–	1
а3	–	1
а4	а1	2
а5	а1	2
а6	а1	2
а7	а3, а6	3
а8	а3, а6	3
а9	а3, а6	3
а10	а2, а4, а9	3
а11	а2, а4, а9	3
(а12)	а8, а11	4

 

На основе преобразованной структурной таблицы строится сетевой график (направленный граф) комплекса работ. Работы, обозначаемые а₁, а₂ …а_n, на графике изображаются с помощью стрелок (дуг), а события, состоящие в завершении предшествующих и начале последующих работ А₁, А₂ …, изображают в виде кружочков (узлов графика). Алгоритм построения сетевого графика покажем на примере табл. 2 (рис. 3).

Событие начала выполнения комплекса работ обозначено А₁. В этот момент может быть начато выполнение работ а₁, а₂, а₃ (см. стрелки графика). Для начала выполнения работ а₄, а₅, а₆ (второго ранга) достаточно завершить выполнение работы а₁, то есть по ее завершению наступает событие А₂. Чтобы наступило следующее событие А₃, должны быть завершены работа а₃, начавшаяся после события А₁, и работа а₆, начавшаяся после события А₂. Продолжая рассуждать аналогичным образом, строим все последующие события А₄, А₅, А₆ и соединяем их стрелками, обозначающими работы с учетом моментов их начала и окончания.

Наличие фиктивных работ (в данном случае а₉) не изменяет алгоритм составления сетевого графика. Событие А₆ означает окончание всех работ сетевого графика, т.е. завершение выполнения всего комплекса работ. График, приведенный на рис. 2, называют структурным сетевым графиком, так как он отражает только логическую последовательность выполнения работ. Для решения задач анализа и синтеза комплекса работ, сетевой график должен быть дополнен информацией о времени выполнения всех входящих в него работ и требуемыми для их выполнения ресурсами.

 

Упражнения

По исходным данным таблицы 3 определить ранги всех работ и построить сетевой график.

Таблица 3

№ задания	Обозначение работ	Опираются на работы	№ задания	Обозначение работ	Опираются на работы
1	2	3	1	2	3
1	а1 а2 а3 а4 а5 а6 а7 а8	– – а1 а2 а2 а1 а1 а1	2	а1 а2 а3 а4 а5 а6 а7 а8	– – а1 а1 а4 а4 а2, а6 а3, а5, а7
Продолжение табл. 3
	а9 а10 а11 а12 а13 а14 а15 а16 а17 а18	а3, а4 а6, а7 а6, а7 а8, а9, а10 а3, а4 а3, а4 а3, а4 а11, а12 а5, а15, а16 а11, а12		а9 а10 а11 а12 а13	а2, а6 а4 а4 а11, а10, а9, а8 а11, а10, а9, а8
3	а1 а2 а3 а4 а5 а6 а7 а8 а9 а10 а11 а12 а13 а14	– – – а3 а1, а4 а3 а5, а6 а3 а3 а2, а7, а8 а2, а7, а8 а9, а10, а11 а9, а10, а11 а9, а10, а11	4	а1 а2 а3 а4 а5 а6 а7 а8 а9 а10 а11 а12 а13 а14 а15	– – – а3 а3 а1 а2, а5, а6 а1 а4, а7, а8 а1 а10 а1 а12 а12 а9, а13, а14
5	а1 а2 а3 а4 а5 а6 а7 а8 а9 а10 а11 а12 а13 а14 а15 а16	– – – а1 а3 а3 а6 а2, а4, а5, а7 а2, а4, а5, а7 а8 а8 а8 а8 а6 а13, а14 а9, а10	6	а1 а2 а3 а4 а5 а6 а7 а8 а9 а10 а11 а12 а13 а14 а15 а16	– – – а3 а3 а2, а4 а1, а5, а6 а1, а5, а6 а8 а1, а5, а6 а8 а9, а7 а12, а10, а11 а8 а13 а13
Продолжение табл. 3
7	а1 а2 а3 а4 а5 а6 а7 а8 а9 а10 а11 а12	– – а2 а3 а4 а2 а5, а6 а5, а6 а2 а2 а1 а9, а7, а8	8	а1 а2 а3 а4 а5 а6 а7 а8 а9 а10 а11 а12 а13 а14	– – – а3 а2, а4 а2, а4 а3 а2, а4 а7, а8 а7, а8 а1, а5 а6, а9, а10, а11 а1, а5 а1, а5
9	а1 а2 а3 а4 а5 а6 а7 а8 а9 а10 а11 а12 а13 а14	– – – – а4 а4 а1 а2, а7 а2, а7 а2, а7 а10 а5, а3, а8, а11 а9, а12 а5, а3, а8, а11	10	а1 а2 а3 а4 а5 а6 а7 а8 а9 а10 а11 а12 а13 а14	– – – – а4 а2 а5, а3, а6 а2 а2 а9 а7, а8, а10 а9 а9 а1
11	а1 а2 а3 а4 а5 а6 а7 а8 а9 а10 а11 а12 а13 а14	– – – а3 а3 а4 а2 а2 а1, а8 а1, а8 а7, а10 а9 а9 а3	12	а1 а2 а3 а4 а5 а6 а7 а8 а9 а10 а11 а12 а13 а14	– – – а1 а2, а4 а2, а4 а5, а3 а2, а4 а6, а7 а9 а9 а9 а8, а10 а8, а10
Окончание табл. 3
13	а1 а2 а3 а4 а5 а6 а7 а8 а9 а10 а11 а12 а13 а14	– – – а2 а2 а1, а5 а2 а3, а4 а8 а8 а6 а6 а11 а7, а9, а12, а13	14	а1 а2 а3 а4 а5 а6 а7 а8 а9 а10 а11 а12 а13 а14 а15	– – – а2 а2 а3, а4 а3, а4 а3, а4 а8 а8 а10 а7, а9, а11 а7, а9, а11 а7, а9, а11 а14, а13, а12
15	а1 а2 а3 а4 а5 а6 а7 а8 а9 а10 а11 а12 а13 а14 а15	– – а2 а1, а3 а1, а3 а1, а3 а2 а2 а8 а8 а10 а4, а7 а4, а7 а5 а6, а13, а14	16	а1 а2 а3 а4 а5 а6 а7 а8 а9 а10 а11 а12 а13 а14 а15	– – а2 а1, а3 а1, а3 а1, а3 а5 а6, а7 а2, а8 а2, а8 а2, а8 а6, а7 а6, а7 а5 а13, а14, а15
17	а1 а2 а3 а4 а5 а6 а7 а8 а9 а10 а11 а12 а13 а14 а15	– – – а3 а4, а1 а3 а5, а6 а3 а3 а7, а8 а10 а9, а11 а9, а11 а10 а10	18	а1 а2 а3 а4 а5 а6 а7 а8 а9 а10 а11 а12 а13 а14 а15	– – – а1 а3 а3 а6 а2, а4, а5, а7 а2, а4, а5, а7 а8 а8 а8 а8 а6 а13, а14

 

Скачано с www.znanio.ru