Построение таблиц истинности по функциям

Практическая работа №4

Тема: Построение таблиц истинности по функциям

Цель:

- освоение алгоритма построения таблиц истинности для логических функций;

 - научиться определять и анализировать функции проводимости переключательных схем.

Вид работы: индивидуальный

Время выполнения: 2 часа.

Теоретические сведения

Логическая функция - это функция, в которой переменные принимают только два значения: логическая единица или логический ноль. Истинность или ложность сложных суждений представляет собой функцию истинности или ложности простых. Эту функцию называют булевой функцией суждений f (a, b).

Для обозначения новых высказываний наиболее часто используются базовые логические операции, выражаемые словами «И», «ИЛИ», «НЕ».

Любая логическая функция может быть задана с помощью таблицы истинности, в левой части которой записывается набор аргументов, а в правой части - соответствующие значения логической функции. При построении таблицы истинности необходимо учитывать порядок выполнения логических операций.

Порядок выполнения логических операций в сложном логическом выражении:

1.     инверсия;

2.     конъюнкция;

3.     дизъюнкция;

4.     импликация;

5.     эквивалентность.

Для изменения указанного порядка выполнения операций используются скобки.

Составленное высказывание, образованное в результате операции логического умножения (конъюнкция), истинно тогда и только тогда, когда истинны входящие в него простые высказывания. Конъюнкция может обозначаться: «И», ^, *, &.

Таблица истинности – это таблица, в левой части которой записывается набор аргументов, а в правой части - соответствующие значения логической функции.

Таблица истинности – это таблица, определяющая значение сложного высказывания при всех возможных значениях простых высказываний.

Таблицу, показывающую, какие значения принимает составное высказывание при  всех сочетаниях (наборах) значений входящих в него простых высказываний, называют таблицей истинности составного высказывания.

Составные высказывания в алгебре логики записываются с помощью логических выражений. Для любого логического выражения достаточно просто построить таблицу истинности.

Таблица 3 - Таблицы истинности (при всех возможных значениях логических переменных):

Ход работы

Алгоритм построения таблиц истинности для сложных выражений следующий:

­       Определить количество переменных (простых выражений);

­       Определить количество логических операций и последовательность их выполнения.

­       Определить количество строк:

количество строк = 2^a + строка для заголовка, где a – количество логических переменных.

­       Определить количество столбцов: количество столбцов = количество переменных + количество логических операций;

­       Заполнить столбцы результатами выполнения логических операций в обозначенной последовательности с учетом таблиц истинности основных логических операций.

Пример 1: Построить таблицу истинности для следующего логического выражения

Решение:

­        Простые выражения (логические переменные): А, В, С; (3)

­        Количество логических операций:

­         - инверсия;

­         - операция дизъюнкции;

­         операция конъюнкции. Всего: 3

­        Количество строк: на входе три простых высказывания: А, В, С, поэтому a=3 и количество строк = 2³ +1 = 9.

­        Количество столбцов: 3+3=6

Заполняем столбцы с учетом таблиц истинности логических операций.

Таблица истинности:

Пример 2: Определите истинность составного высказывания состоящего из простых высказываний:

А={Принтер – устройство вывода информации}

В={Процессор – устройство хранения информации}

C={Монитор – устройство вывода информации}

D={Клавиатура – устройство обработки информации}

Установим истинность простых высказываний:

А=1, В=0, С=1, D=0

Определяем истинность составного высказывания:

Пример 3: Доказать равносильность логических выражений:

 и

Таблица истинности

Таблица истинности

Следовательно, =

Пример 3:Запишите логическую функцию, описывающую состояние схемы, составьте таблицу истинности:

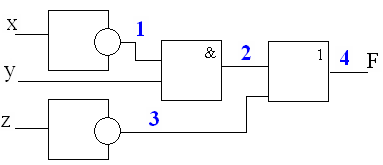
Для записи функции необходимо записать значения на выходе каждого элемента схемы:

1.    

2.    

3.    

4.    

Следовательно, получится функция:

Задания к практической работе

Задание 1. Построить таблицу истинности для логических выражений:

1)    а);                            б) ;

2)    а);                     б) ;

3)    а);                       б) ;

4)    а);                            б) ;

5)    а);                          б) ;

6)    а);                            б) ;

7)    а);                            б) ;

8)    а);              б) .

Задание 2. Определите истинность составного высказывания состоящего из простых высказываний:

1)    А = {Принтер – устройство ввода информации},

В = {Процессор – устройство обработки информации},

С = {Монитор – устройство хранения информации},

D = {Клавиатура – устройство ввода информации}.

Установим истинность простых высказываний: А=1, В=0, С=1, D=0. Определите истинность составного высказывания.

2)    А = {Принтер – устройство ввода информации},

В = {Процессор – устройство обработки информации},

С = {Монитор – устройство хранения информации},

D = {Клавиатура – устройство ввода информации}.

Установим истинность простых высказываний: А=1, В=0, С=1, D=0. Определите истинность составного высказывания.

3)    А = {Принтер – устройство ввода информации},

В = {Процессор – устройство обработки информации},

С = {Монитор – устройство хранения информации},

D = {Клавиатура – устройство ввода информации}.

Установим истинность простых высказываний: А=1, В=0, С=1, D=0. Определите истинность составного высказывания.

4)     А = {Москва – столица России},

В = {Число 27 является простым},

     С = {Волга впадает в Каспийское море}.

Установим истинность простых высказываний: А=1, В=0, С=1. Определите истинность составного высказывания.

А = {Сегодня светит солнце},

В = {Трава растет}.

Установим истинность простых высказываний: А=1, В=0. Определите истинность составного высказывания.

5)    А = {Если идет дождь, то солнце не светит},

В = {Если ветер дует, то нет дождя}.

Установим истинность простых высказываний: А=1, В=0. Определите истинность составного высказывания.

6)     А = {Сегодня суббота},

В = {Сегодня пасмурно},

С = {Я буду читать книгу}.

Установим истинность простых высказываний: А=1, В=0, С=1. Определите истинность составного высказывания.

7)     А = {Мышь больше слона},

В = {Молодые лошади называются щенятами},

С = {6 больше 8}.

Установим истинность простых высказываний: А=1, В=0, С=1. Определите истинность составного высказывания.

8)     А = {На улице идет дождь},

В = {На улице светит солнце},

С = {На улице пасмурная погода},

     D = {На улице идет снег}.

Установим истинность простых высказываний: А=1, В=0, С=1, D=0. Определите истинность составного высказывания.

Задание 3. Запишите логическую функцию, описывающую состояние схемы, составьте таблицу истинности:

Контрольные вопросы и задания

1.           Что такое дизъюнкция? Когда истинна дизъюнкция?

2.           Что такое конъюнкция? Когда истинна конъюнкция?

3.           Как определить количество строк в таблице истинности?

4.           Назвать приоритет логических операций.

5.           Какое количество логических функций двух аргументов существует и почему?

6.           Какие логические функции двух аргументов имеют свои названия?

7.           Какое существует количество логических функций трех аргументов?

8.           Какие законы логики вы знаете?

9.           Какие существуют правила преобразования логических выражений?

10.       Скачано с www.znanio.ru