Поверхности и объемы призм. Геометрия 10-11 класс.

Поверхности и объемы  призм.

Справочный материал.

Куб.

a – ребро куба ;       d – диагональ куба. 

                                              d² = 3a²      d=a√3

S_бок.– боковая поверхность куба.     S_{куба. .}– полная поверхность куба. 

                           S_бок. = 4а²     ;       S_куба. = 6а²           

V – объем куба.              V= а³

Прямоугольный параллелепипед.

a, b, c – длина, ширина, высота (измерения) прямоугольного параллелепипеда.

d – его диагональ.              d² = a² + b²  +c²

S_бок.– боковая поверхность параллелепипеда.

S_бок. = 2 ( ac +bc)     или     S_бок. =P_осн.∙h,   P_осн.. – периметр (сумма сторон) основания,   h - высота параллелепипеда.

S_пар.– полная поверхность параллелепипеда.     S_пар.=2(ac+bc+ab)    или

S_пар.= S_бок. +2 S_{осн. , где}     S_{осн. – площадь основания}

V – объем параллелепипеда. V= a∙b∙c     или     V= S_осн.∙ h

Призма.

S_бок.– боковая поверхность призмы

S_бок. =P_осн.∙h,   P_осн.. – периметр (сумма сторон) основания,   h - высота призмы.

S_пр.– полная поверхность призмы.                             S_пр.= S_бок. +2 S_осн

V – объем призмы         V= S_осн.∙ h    S_{осн. – площадь основания,}     h - высота призмы.

1). Разобрать решение задач    1.1,  1.2,  2.1 :

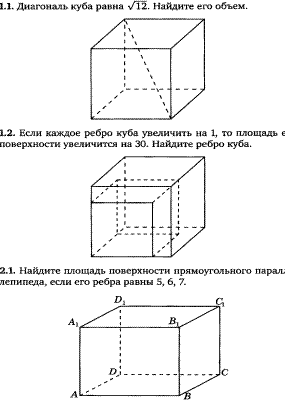
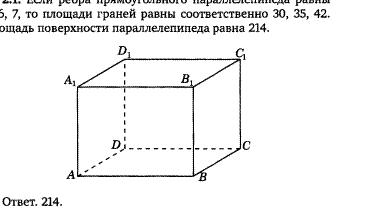
Решение задачи 2.1.

             Если ребра прямоугольного параллелепипеда

               равны  5, 6,

2). Решить самостоятельно №1, №2, №3.

Задача 1.Диагональ куба равна  √48. Найти объем куба.

Задача 2. Если каждое ребро куба увеличить на 2, то площадь поверхности  куба увеличится на 144. Найти ребро куба.

Задача 3. Найти площадь поверхности и объем прямоугольного параллелепипеда, если его измерения которого равны  2,  8,  11.

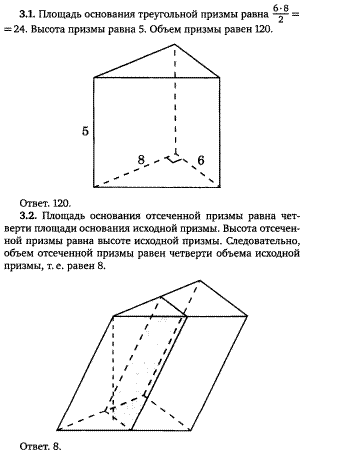
3). Разобрать решение  задач 3.1, 3.2.

Решение задач 3.1 и 3.2.

4). Решить самостоятельно№4,  №5.

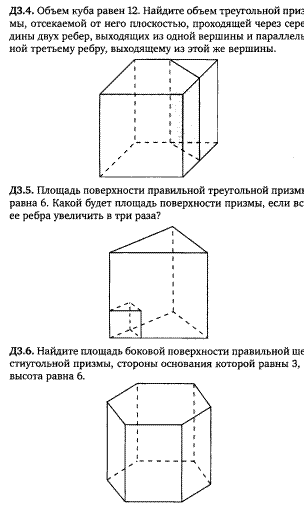
Задача 4. Основание прямой треугольной призмы – прямоугольный треугольник  с катетом 8 и гипотенузой 10. Боковое ребро призмы  равно 18. Вычислить объем призмы.

Задача 5. Через среднюю линию основания треугольной призмы , объем которой равен 124, проведена плоскость, параллельно боковому ребру. Найти объем оставшейся части после удаления отсеченной малой треугольной призмы.

5). Разобрать решение  задач  5.1.

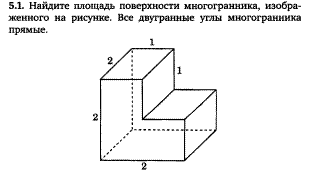
Решение  задачи 5.1.

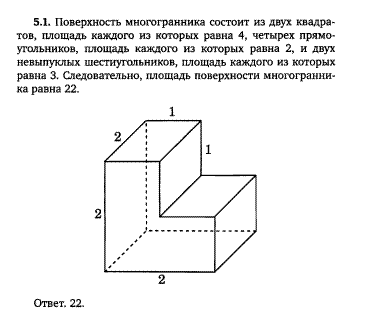
5). Решить самостоятельно№6, №7, №8.

Задача 6.  Вычислить площадь поверхности и объем.

Задача 7. Вычислить площадь поверхности и объем.

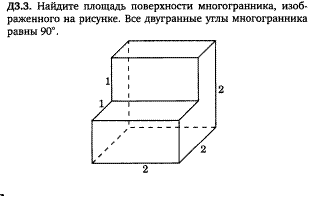
Задача 8.

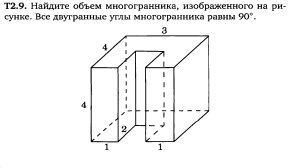
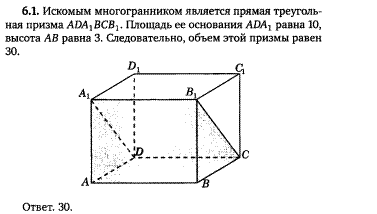
6). Разобрать решение задачи 6.1.

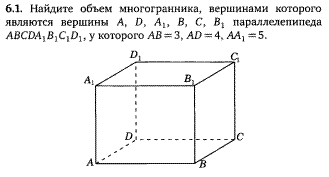
Решение задачи 6.1.

                      6). Решить самостоятельно №9  -  №28.

Задача 9.  Найти объем  и поверхность многогранника, вершинами  которого  являются вершины D, A₁, D₁, C₁, B₁, C  параллелепипеда ABCDA₁B₁C₁D₁, у которого  BA=8, BC=12, BB₁=5

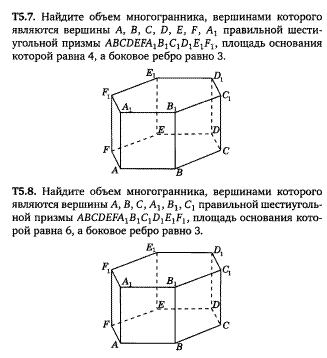
Задача 10 и 11    (5.7 и 5.8).

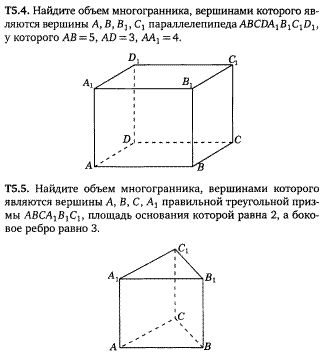
Задача 12 и 13    (5.4  и  5.5).

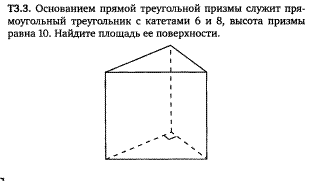
Задача 14 , 15 ,16   (3.3, 3.5, 3.6 ).

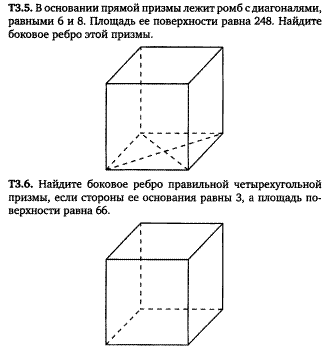
Задача 17 , 18 ,19  (2.5, 2.6 ,2.7).

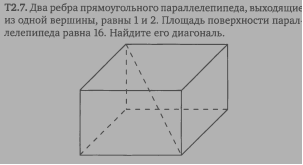
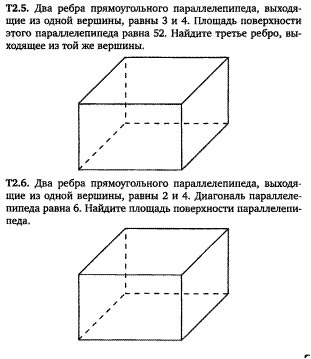
Задача 20  (3.9)

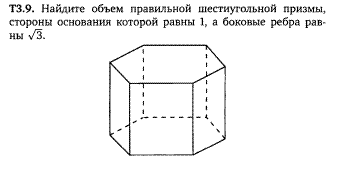
Задача 21  (1.5)

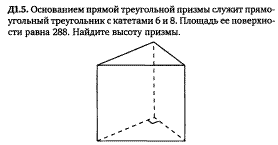
Задача 22  (2.1)

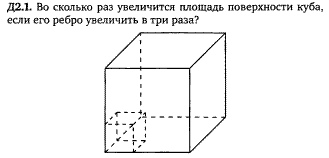
Задача 23  (2.3)

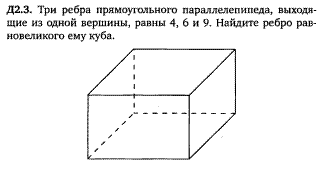
Задача 24  (2.7)

Задача 25  (3.1)

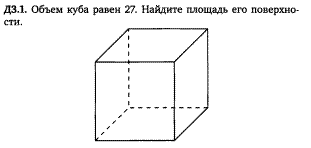
Задача 26, 27, 28  (3.4, 3.5, 3.6)

Ответы на задачи по теме «Призма».