Тема: Одночлены и многочлены

( При умножения одинаковых оснований (чисел или букв) в степень нужно показатели степеней сложить, а основание оставить без изменений; при деление – вычесть степени; при возведении степень в степень – умножить показатели степеней.)

1.     Найдите значение выражения:

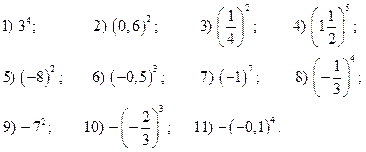
2. Вычислите значение выражения:

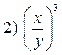 при х = 12 и у = –0,5.              при        х = 0 и у = –23;

 при х = 0,9 и у = 1,1.

3. Упростите выражение:

4. Найдите значение выражения, используя свойства степеней:

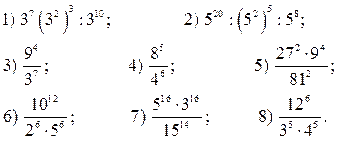
5. Упростите выражение:

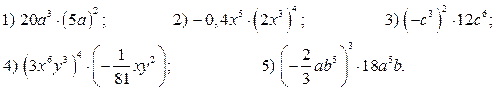
6. Приведите многочлен к стандартному виду:

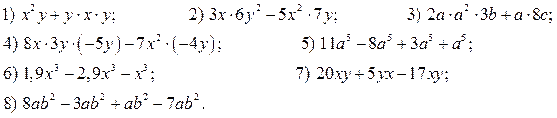
7. Приведите подобные члены и укажите степень многочлена:

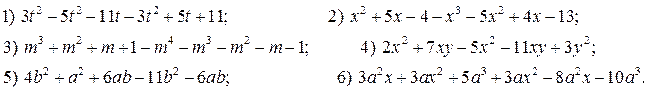
8. Упростите выражение (распределительное свойство):

Тема: Разложение многочленов на множители

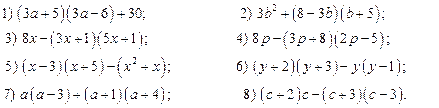
1. Разложите многочлен на множители (сгруппировать и вынести за скобки общий множитель: например ах+вх+ас+вс = (ах+вх)+(ас+вс) = х(а+в) +с(а+в) = (х+с)(а+в)) :

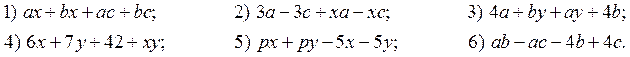
2. Разложите на множители:

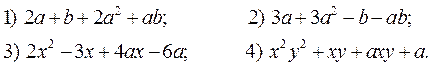
3. Преобразуйте в многочлен (раскрыть скобки, используя формулы сокращенного умножения, упростить (привести подобные слагаемые)):

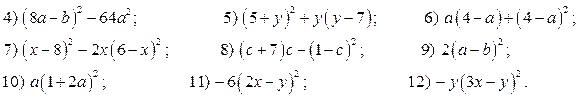
4. Представьте многочлен в виде квадрата двучлена (формула сокращенного умножения - свернуть):

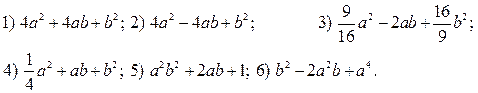
5. Разложите на множители (формула сокращенного умножения):

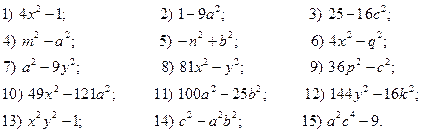
6. Представьте в виде произведения (формула сокращенного умножения - свернуть):

:

Тема: Алгебраические дроби

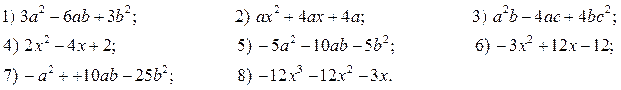
1. Сократите дробь (17-24 задания: свернуть, либо расписать, используя формулы сокращенного умножения или вынести общий множитель за скобки; сократить одинаковые части):

2. Выполните сложение:

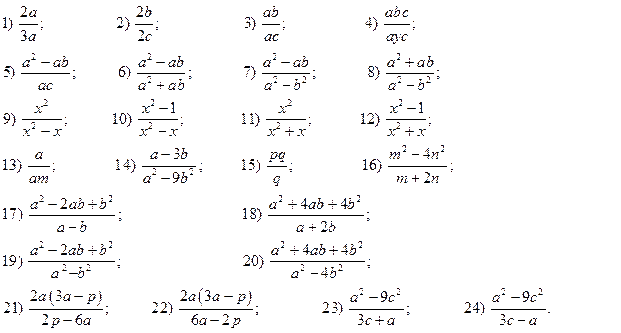
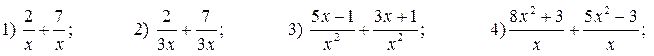
3. Выполните действия:

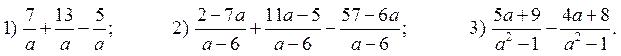
4. Упростите выражение (формулы сокращенного умножения – либо раскрыть, либо свернуть, так чтобы можно было либо сократить, либо знаменатель получился одинаковым. Так как выполнить сложение и вычитание обыкновенных дробей с разными знаменателями нельзя. А сокращать можно только если выполняется деление либо умножение двух обыкновенных дробей.):

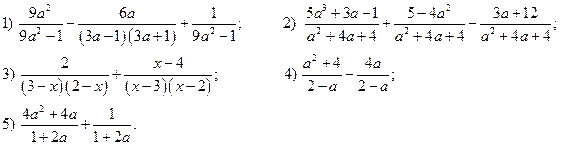
5. Выполните сложение или вычитание:

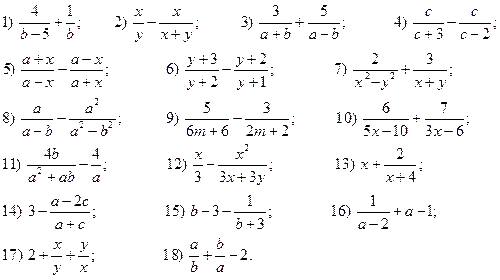
6.Выполните умножение или деление (упростите выражение):

Тема: Линейная функция и ее график

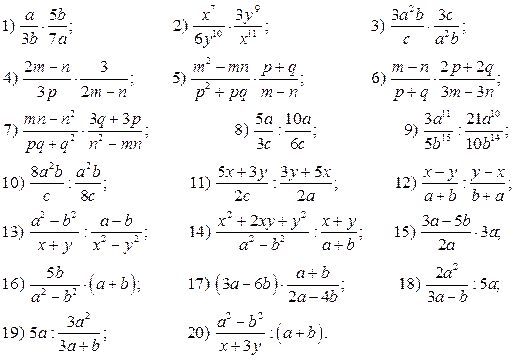
1. Построите систему координат (возьмите единичные отрезки на осях, равные 2 клеткам). Отметьте в координатной плоскости точки и обозначьте их:

1) (2; 4), (5; –3), (–1; 1), (–2; –3);

2) (2,5; 1), (2,5; –1), (0,4; 3,5), (–0,4; 3,5);

2. Найдите значения функции, заданной формулой:

1)  для значений аргумента, равных –3;

2)  для значений аргумента, равных 1,5;

3. Найдите значение аргумента, при котором:

1) функция  принимает значение, равное 12;

2) функция принимает значение, равное .

4. Постройте в одной системе координат графики функций:

у = -3х и у = 4х-2

а) запишите координаты точки их пересечения;

б) выпишите координаты пересечения каждого графика с осями координат.

5. Постройте график функции, заданной формулами:

1)

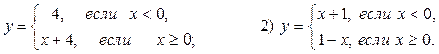
Является ли функция линейной?

6. Задайте формулой линейную функцию, если известны угловой коэффициент k

соответствующей прямой и координаты точки A, через которую она проходит:

Пример: Задайте формулой линейную функцию если известны угловой коэффициент k соответствующей прямой и координаты точки А через которую она проходит:
а) k=2/5, A(-10;-4);

Уравнение линейной функции у = кх + в.
Координаты точки соответствуют этому уравнению.
а) k=2/5, A(-10;-4).
-4 = (2/5)*(-10) + в.
в = -4 +(2*10/5) = -4 + 4 = 0.
Уравнение имеет вид у = (2/5)х.

Тема: Системы двух уравнений с двумя неизвестными

1. Выразите в следующих уравнениях х через у и у через х:

2. Решите систему уравнений(способ подстановки):

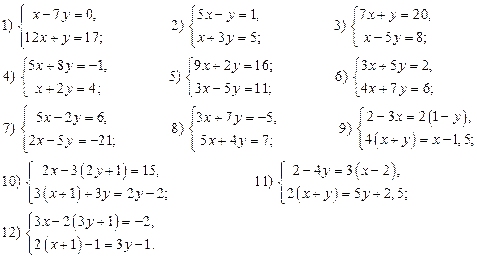
2. Вычислите координаты точки пересечения прямых (приравнять два уравнения и посчитать чему равна переменная х, подставить в любое уравнение значение вместо х и найти переменную у, то есть (1 пример) 3х+6 = -2х-1 решить уравнение и найти х. А потом в любое поставить значение х и найти у. Пара чисел и будет являть пересечением двух прямых)):

 и     2) 4х-3у= -1  и  3х + 2 у =12.

2.     Запишите с помощью системы уравнений следующую ситуацию (неизвестное число принять за переменную.)

 Например:

 А) Сумма двух чисел равна 17. Одно из чисел на 7 меньше другого.

Так как числа не известны примем их за переменные х и у и получим.

Х + У = 17 - Сумма двух чисел равна 17;

Х + У – 7 = 17 - Одно из чисел на 7 меньше другого.

Получим систему:

Х + У = 17,

Х + У – 7 = 17.

б) Разность двух чисел равна 12. Одно из них больше другого в 4 раза.

в) В классе 36 учеников. Девочек на 3 меньше, чем мальчиков.

г) Периметр прямоугольника 400 м. Длина его в 3 раза больше ширины.

д) 4 боксера тяжелого веса и 5 боксеров легкого веса вместе весят 730 кг. Спортсмен тяжелого веса весит на 70 кг больше спортсмена легкого веса.

е) Таня заплатила за 3 тетради и 2 карандаша 580 р., а Лена за 5 таких же тетрадей и 1 карандаш — 780 р.

4. Составьте систему уравнений и решите задачу (решить способом подстановки):

1) Расстояние между домами, где живут Андрей и Борис, 1500 м. Школа находится между их домами, причем от дома Андрея она на 300 м дальше, чем от дома Бориса. На каком расстоянии от школы находится дом каждого мальчика?

2) У Толи 18 монет по 2 р. и 5 р. на сумму 97 р. Сколько монет каждого достоинства у Толи?

3) В магазине продаются тетради по 96 листов и по 24 листа. Во всех тетрадях, купленных Сашей, 528 листов. Сколько толстых и сколько тонких тетрадей купил Саша, если все купленные им толстые тетради содержат на 48 листов больше, чем все тонкие?

4) Поезд прошел первый перегон за 2 ч, а второй за 3ч. Всего за это время он прошел 330 км. Найдите скорость поезда на каждом перегоне, если на втором перегоне она была на 10 км/ч больше, чем на первом.

5) За 3 ч против течения лодка проплыла на 5 км больше, чем за 2 ч по течению. Скорость лодки против течения составляет 0,75 ее скорости по течению. Какое расстояние прошла лодка за это время?