Практическая работа №11 по дисциплине "ИТ в ПД"

Практическая работа №11

Моделирование в системе  Mathcad

Цель работы:

­          исследование возможностей применения программного пакета MATHCAD  для математического моделирования задачи использования мощностей оборудования;

­          закрепление знаний о методах моделирования и обработке результатов случайных процессов для решения технических задач.

 Время выполнения работы  2 часа.

Оборудование, приборы, аппаратура, материалы: персональный компьютер, Visio 2007.

Ход выполнения работы:

1. Условие задачи:

Предприятие имеет n моделей машин М₁,М₂,…, М_n различных мощностей. На этих машинах предприятие выпускает m видов продукции П₁, П₂,…, П_m. Известны производительность каждой  i-ой машины по выпуску j- го вида продукции − b_ij и стоимость единицы времени, затрачиваемого i-ой машиной на выпуск одного изделия  j- го вида продукции − c_ij.

Задан план по времени и номенклатуре: T − время работы каждой машины, при этом, продукции j- го вида должно быть выпущено не менее N_j единиц.

Требуется составить такой план работы оборудования, чтобы обеспечить минимальные затраты на производство.

Для решения поставленной задачи сформулируем её математическую модель, первоначально сведя исходные данные в следующую таблицу:

Для решения сформулированной задачи составим ее математическую модель.

Математическая модель задачи использования мощностей оборудования. Для построения математической модели задачи:

1. Определим неизвестные и их количество.

Обозначим х_ij − время работы i- ой машины (i=1,2,..,n) по выпуску j- го вида продукции (j=1,2,…,m), обеспечивающее минимальные затраты на производство при соблюдении ограничений по общему времени работы машин Т и заданному количеству продукции j-го вида N_j.

2. Запишем целевую функцию F(X) − затраты на производство, которую необходимо минимизировать.

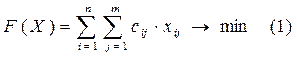
3. Сформулируем ограничения рассматриваемой задачи.

3.1. Ограничение по времени работы каждой машины.

По условию задачи все машины работают заданное время T, поэтому данное ограничение можно представить в следующем виде:

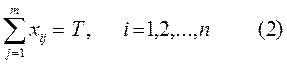
3.2. Ограничение по заданному количеству продукции имеет вид:

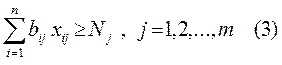
3.3. Условие неотрицательности переменных:

Таким образом, целевая функция (1) и ограничения (2−4) образуют математическую модель задачи использования мощностей оборудования.

2. Пример выполнения

Постановка задачи. Предприятие имеет 3 станка М₁, М₂, М₃ различной производительности. На этих станках предприятие выпускает 4 вида продукции П₁, П₂,П₃,П₄. Известны производительность каждой i-ой машины по выпуску j- го вида продукции b_ij и стоимость единицы времени, затрачиваемого i-й машиной на выпуск одного изделия  j- го вида продукции − c_ij. Задан план по времени и номенклатуре: T − время работы каждой машины, при этом, продукции j- го вида должно быть выпущено не менее N_j единиц.

Требуется составить такой план работы оборудования, чтобы обеспечить минимальные затраты на производство. Числовые данные приведены в следующих таблицах.

Таблица 1. Данные для задачи использования мощностей

Таблица 2. Данные для задачи использования мощностей

Все станки работают заданное время Т, равное 1000 временных единиц.

Математическая модель задачи использования мощностей оборудования. Для построения математической модели задачи:

1. Определим неизвестные и их количество:

Обозначим х_ij  − время работы i- го станка (i=1,2,3) по выпуску j - го вида продукции (j=1,2,3,4), обеспечивающее минимальные затраты на производство при соблюдении ограничений по общему времени работы машин Т и заданному количеству продукции N_j.

2. Определим целевую функцию F(X) – суммарные затраты на производство, которую необходимо минимизировать.

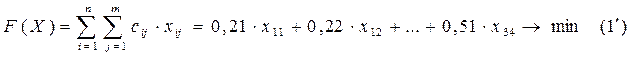
3. Запишем ограничения нашей задачи:

3.1. Ограничение по времени работы каждой машины.

По условию задачи станки работают заданное время T, поэтому данное ограничение можно представить в следующем виде:

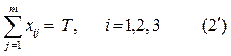
3.2. Ограничение по заданному количеству продукции имеет вид:

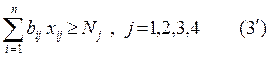
3.3. Условие не отрицательности переменных:

Таким образом, целевая функция (1´) и ограничения (2´− 4´) образуют математическую модель задачи использования мощностей оборудования.

В данной постановке задачи предполагается, что количество выпускаемой продукции должно быть, по крайней мере, не менее N_j. В некоторых случаях не допускается превышение плана по номенклатуре; очевидно в этом случае в ограничениях по количеству продукции необходимо использовать знак равенства.

3. Решение задачи с помощью математического пакета MathCad. Для решения задачи в среде пакета MathCad :

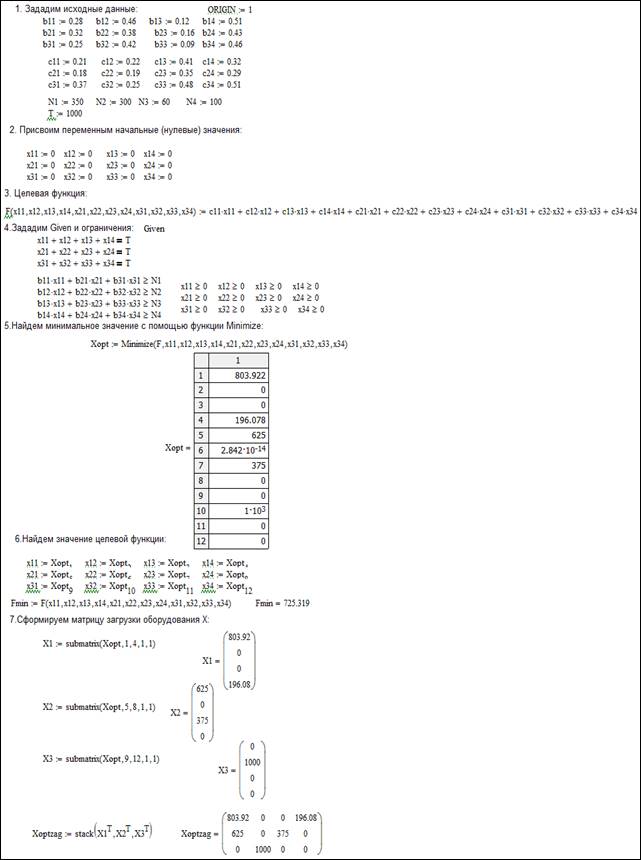
1)     Задайте исходные данные.

2)     Присвойте переменным начальные нулевые значения.

3)     Определите целевую функцию.

4)     Введите служебное слово Given и, после него, систему ограничений.

5)     Найдите оптимальное решение с помощью функции Minimize.

6)     Вычислите значение целевой функции.

7)     Сформируйте матрицу загрузки оборудования Х.

8)     Сделайте выводы по выполненной работе.

9)     Сохраните результаты вычислений в своей папке.

Используемые источники:

1. Михеева Е.В., Информационные технологии в профессиональной деятельности. – М.: Издательский центр «Академия», 2012.
2. Михеева Е.В., Практикум по Информационным технологиям в профессиональной деятельности. – М.: Издательский центр «Академия», 2007.


3. Скачано с www.znanio.ru