
Работа 4. ПРОГРАММИРОВАНИЕ РАЗВЕТВЛЯЮЩЕГОСЯ
ВЫЧИСЛИТЕЛЬНОГО ПРОЦЕССА
Задание 1. Задать кусочно-непрерывную функцию f(x) с помощью условной функции ЕСЛИ и построить график f(x) для х от –1 до 5 с шагом 0,5
Пример:
|
|
|
функция |
|
a |
|
f(x) = |
|
|
если в остальных случаях |
–1 |
Примечание: выражение для f(x) читается
так: если ![]() , то
, то ![]() , иначе
, иначе ![]()
Решение:
1. В ячейку А1 внести название переменной: x, в ячейку В1 внести обозначение функции: f(x).
2. Начиная с ячейки А2, заполнить столбец значениями х, начиная с –4 до 6, с шагом 0,5, используя автозаполнение.
3. В ячейку В2 внести формулу, вычисляющую значение f(x) в зависимости от условия и протянуть для всех х, используя автозаполнение.
Значение y вычисляется с помощью функции ЕСЛИ. Она содержит три параметра, заключенных в скобки и разделенных точкой с запятой :

Тогда для примера формула для ячейки В2 будет следующей:
=ЕСЛИ( A2<=-1 ; SIN(A2) ; EXP(-A2) )
Вид решения: Построить точечную диаграмму
|
|
A |
B |
|
|
1 |
x |
f(x) |
|
|
2 |
-4 |
0,756802495 |
|
|
3 |
-3,5 |
0,350783228 |
|
|
4 |
-3 |
-0,141120008 |
|
|
5 |
-2,5 |
-0,598472144 |
|
|
6 |
-2 |
-0,909297427 |
|
|
7 |
… |
… |
Варианты:
|
№ |
|
|
функция |
|
a |
|
1) |
f(x) = |
|
|
если x>=a в остальных случаях |
1,5 |
|
2) |
f(x) = |
|
|
если >=a в остальных случаях |
1,75 |
|
3) |
f(x) = |
|
|
если в остальных случаях |
2,7 |
|
4) |
f(x) = |
|
|
если в остальных случаях |
3,4 |
|
5) |
f(x) = |
|
|
если в остальных случаях |
0,9 |
|
6) |
f(x) = |
|
|
если в остальных случаях |
3 |
|
7) |
f(x) = |
|
|
если в остальных случаях |
3,2 |
|
8) |
f(x) = |
|
|
если в остальных случаях |
2,4 |
|
9) |
f(x) = |
|
|
если в остальных случаях |
2,9 |
|
10) |
f(x) = |
|
|
если если |
4,75 |
Задание 2. Задать функцию y(x) и построить ее график
Пример:
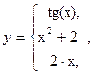
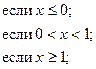
![]()
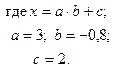
Краткая инструкция по записи функции:
В нашем примере будет две вложенных функции ЕСЛИ. Тогда общая формула будет:
=ЕСЛИ( D2<=0 ; TAN(D2) ; ЕСЛИ( И(0<D2; D2<1) ; D2^2+1 ; 2*D2 ) )
|
|
A |
B |
C |
D |
E |
|
1 |
a |
b |
c |
x |
y |
|
2 |
3 |
-0,8 |
2 |
=A2*B2-C2 |
=ЕСЛИ( D2<=0; TAN(D2) ; ЕСЛИ( И(0<D2; D2<1) ; D2^2+1 ; 2*D2 ) ) |
1)
y = 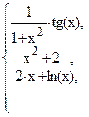
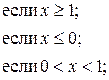
![]()
2)
y = 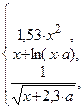
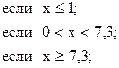
![]()
3)
y = 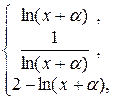
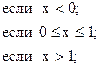
![]()
4)
y = 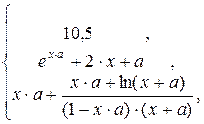
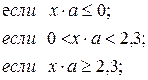
![]()
5)
y = 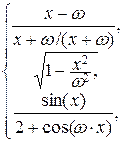
![]()
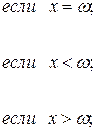
![]()
6)
y = 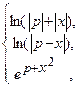
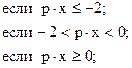
![]()
7)
y = 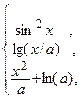
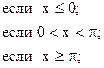
![]()
8)
y = 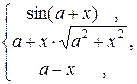
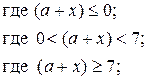
![]()
9)
y = 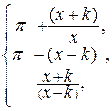
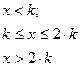
![]()
10. y = 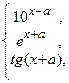
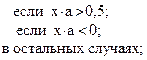
![]()
![]()
11. y = 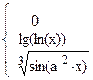
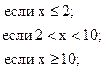
![]()
12. y = 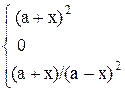
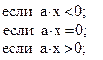
![]()
13. y = 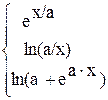
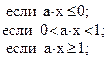
![]()
14. y = 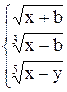
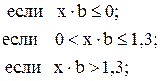
![]()
15. y = 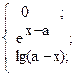
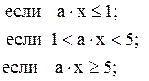
![]()
16. y = 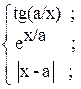
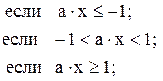
![]()
17. y = 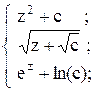
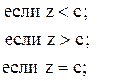
![]()
18. y = 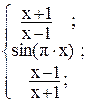
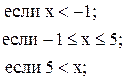
19. y = 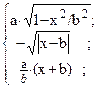
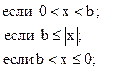
![]()
20. y = 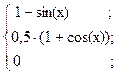
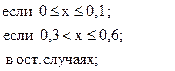
21. y = 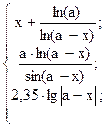
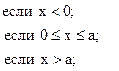
![]()
22. y = 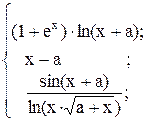
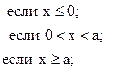
![]()
23. y = 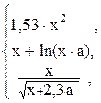
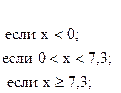
![]()
24. y = 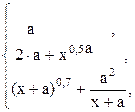
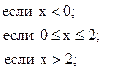
![]()
25. y = 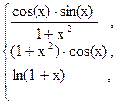
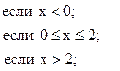
26. y = 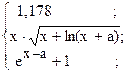
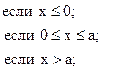
![]()
27. y = 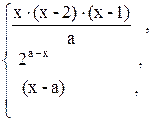
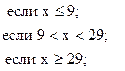
![]()
28. y = 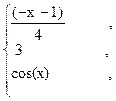
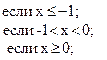
29. y = 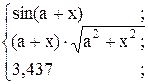
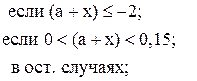
![]()
30. y = 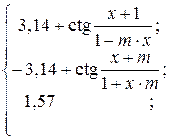
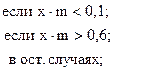
![]()
31. y = 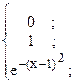
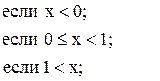
32. y = 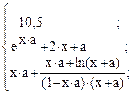
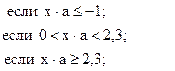
![]()
33. y = 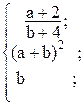
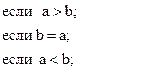
![]()
34. y = 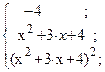
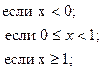
35. y = 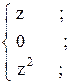
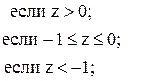
36. N = 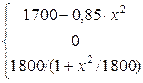
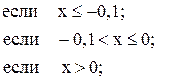
37. Z = 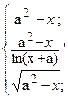
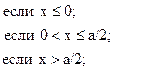
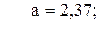
38. y = 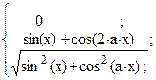
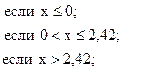
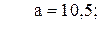
39. x = 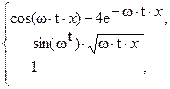
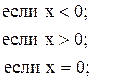
![]()
40. y = 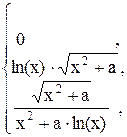
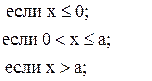
![]()
41. y = 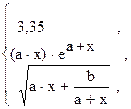
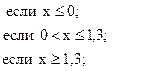
![]()
42. y = 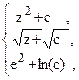
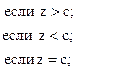
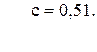
43. y = 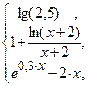
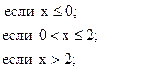
44. y = 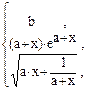
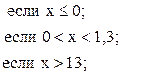
![]()
45. y = 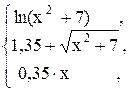
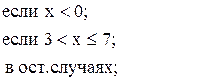
46. y = 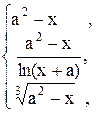
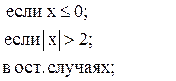
![]()
47. y = 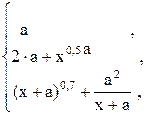
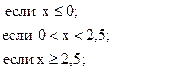
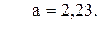
48. y = 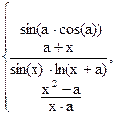
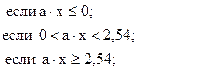
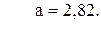
49. y = 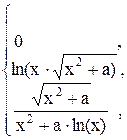
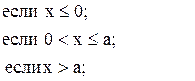
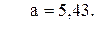
50. y = 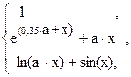
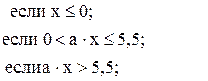
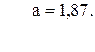
51. y = 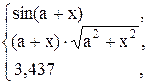
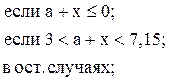
![]()
52. y = 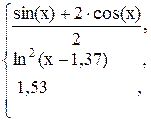
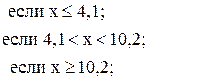
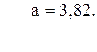
53. y = 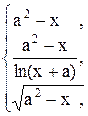
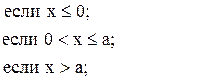
![]()
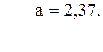
54. z = 
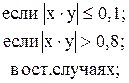
![]()
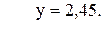
55. z = 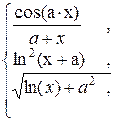
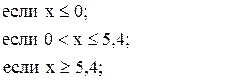
![]()
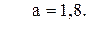
56. z = 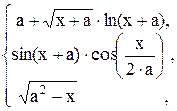
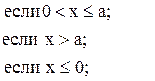
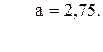
![]()
57. y = 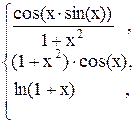
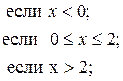
![]()
58. y = 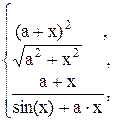
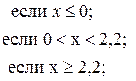
![]()
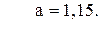
59. y = 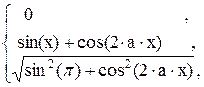
![]()
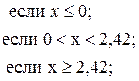
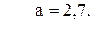
60. y = 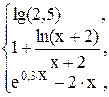
![]()
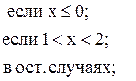
61. a = 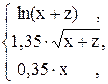
![]()
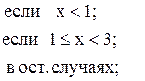
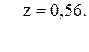
62. y = 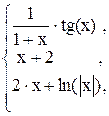
![]()
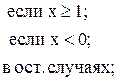
63. b = 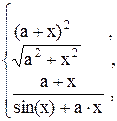
![]()
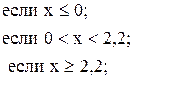
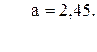
64. y = 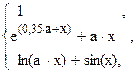
![]()
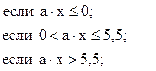
![]() .
.
65. z = 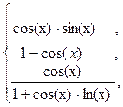
![]()
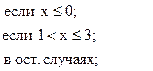
66. z = 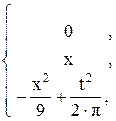
![]()
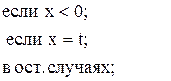
![]()
67. M = 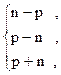
![]()
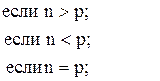
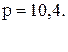
68. y = 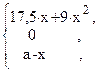
![]()
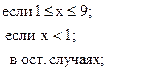
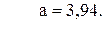
69. f = 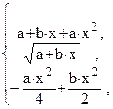
![]()
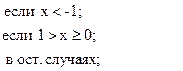
![]()
70. y = ![]()
![]()
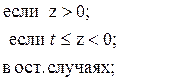
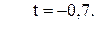
71. j = 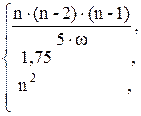
![]()
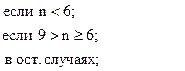
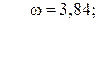
72. y = 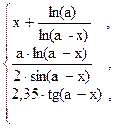
![]()
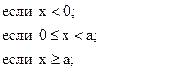
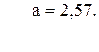
73. a = 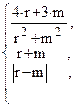
![]()
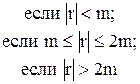
![]()
74. K = 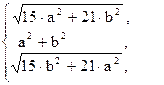
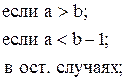
![]()
75. J = 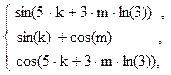
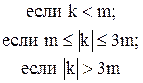
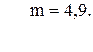
76. y = 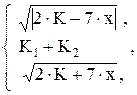
![]()
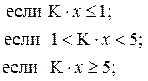
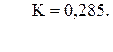
77. j = 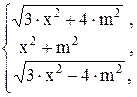
![]()
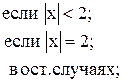
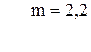
78. n = 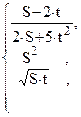
![]()
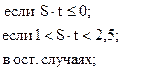
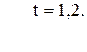
79. J = 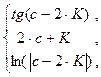
![]()
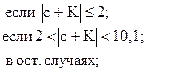
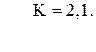
80. d = 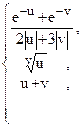
![]()
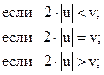
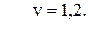
81. l3
= 
![]()
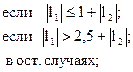
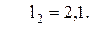
82. f = 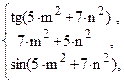
![]()
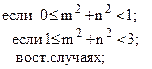
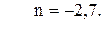
83. n3
= 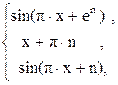
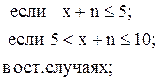
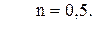
84. R = 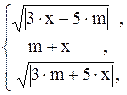
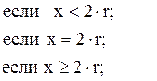
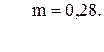
85. l = 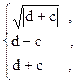
![]()
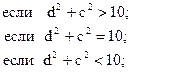
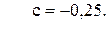
86. m = 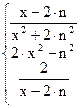
![]()
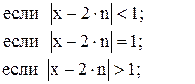
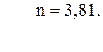
87. S = 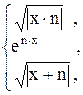
![]()
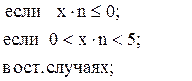
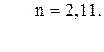
88. l = 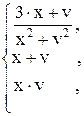
![]()
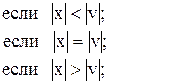

89. K = 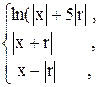
![]()
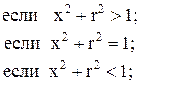
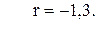
90. K = 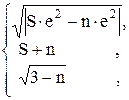
![]()
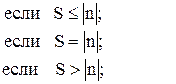
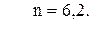
91. m = 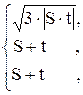
![]()
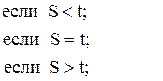
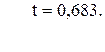
92. j = 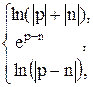
![]()
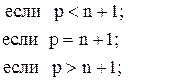
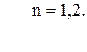
93. i3
= 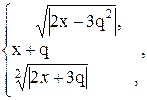
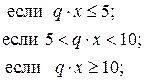
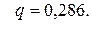
94. m = 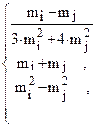
![]()
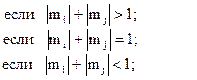
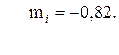
95. n = 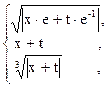
![]()
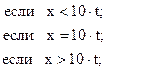
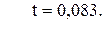
96. l = 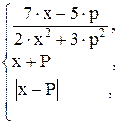
![]()
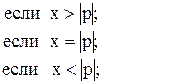
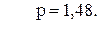
97. S = 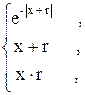
![]()
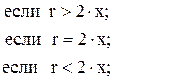
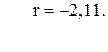
98. K = 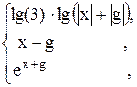
![]()
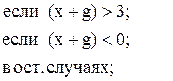
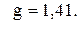
99. m = 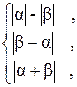
![]()
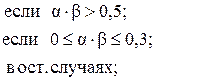
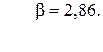
100. V = 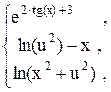
![]()
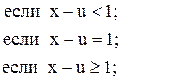
![]()
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.