Практическая работа на тему: " Исследование функции"

Практическая работа №2

Тема: «Исследование функции»

Цель: уметь применять производные функций для ее исследования, пользуясь соответствующими алгоритмами, а также уметь применять таблицу основных производных, формулы дифференцирования: суммы (разности), произведения, частного, вынесения константы из-под знака производной для нахождения производных функций при обосновании этапов решения задач; отработать навыки исследования функций.

Оборудование: ручка, карандаш, линейка, методические рекомендации по выполнению работы.

Методические рекомендации по выполнению практической работы:

Задание №1. Найти промежутки монотонности функции:

а) , б)

Решение:

Воспользуемся алгоритмом:

1) найдем производную данной функции,

2) найдем стационарные точки, приравняв производную к нулю,

3) отметим стационарные точки на числовой прямой и определим знаки производной в каждом из получившихся промежутков,

4) если на промежутке y`>0, то на этом промежутке функция возрастает; если на промежутке y`<0, то на этом промежутке функция убывает.

а) 1) y`= ()` = 3·2x – 0 = 6x,

    2) y` = 0 ⟺ 6x=0

                           x=0 – стационарная точка,

    3) изобразим промежутки монотонности данной функции (рис. 1)

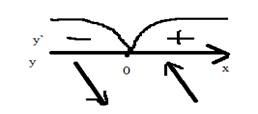
Рис. 1

    4) итак, при  то на этом промежутке функция убывает,

                 при  то на этом промежутке функция возрастает.

б) 1) )` = ()`- ()`-(6x)`+(5)` =

, итак ,

    2) y` = 0 ⟺ =0

                         = ,

                         = - стационарные точки,

    3) изобразим промежутки монотонности данной функции (рис. 2)

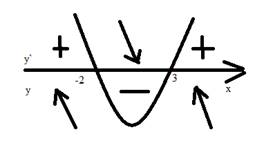
Рис. 2

    4) итак, при  то на этом промежутке функция возрастает,

                   при  то на этом промежутке функция убывает.

Задание №2.  Найти экстремумы функции:

а) , б)

Решение:

Рассмотрим алгоритм:

1) найдем производную данной функции,

2) найдем стационарные точки, приравняв производную к нулю,

3) отметим стационарные точки на числовой прямой и определим знаки производной в каждом из получившихся промежутков,

4) если при переходе через стационарную точку первая производная меняет знак с «плюса» на «минус», то в этой точке наблюдается максимум функции; если при переходе через стационарную точку первая производная меняет знак с «минуса» на «плюс», то в этой точке наблюдается минимум функции.

а) 1)

,

    2) y` = 0 ⟺ 4x – 4=0

                          4x=4

   x=1 – стационарная точка,

    3) отметим стационарную точку на числовой прямой и определим знаки производной в каждом из получившихся промежутков (рис. 3)

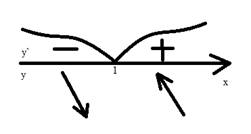
Рис. 3

    4) итак, при переходе через точку x=1, производная меняет знак с «минуса» на «плюс», то в данной точке наблюдается минимум, то есть .

б) 1) )` = ()`- ()`-(2)` =

, итак ,

    2) y` = 0 ⟺ =0

                          x(x – 4) = 0,

                          x = 0 или x – 4 = 0

                          x = 0 или x = 4 – стационарные точки,

    3) отметим стационарные точки на числовой прямой и определим знаки производной в каждом из получившихся промежутков (рис. 4)

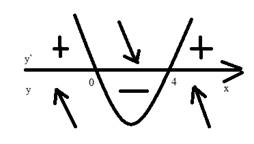
Рис. 4

    4) итак, при переходе через точку x=0, производная меняет знак с «плюса» на «минус», то в данной точке наблюдается максимум, то есть ;

                   при переходе через точку x=4, производная меняет знак с «минуса» на «плюс», то в данной точке наблюдается минимум, то есть

Задание №3. Найдите наименьшее и наибольшее значения функции на отрезке:

а)

б)

Решение:

Алгоритм:

1) найдем экстремумы функции,

2) вычислим значения функции в точках экстремума и на концах отрезка,

3) выберем самое большое значение функции и назовем его , выберем самое маленькое значение функции и назовем его .

а) 1)

     y` = 0 ⟺ =0

                        =0

x=0 – стационарная точка.

Отметим стационарную точку на числовой прямой и определим знаки производной в каждом из получившихся промежутков (рис. 5)

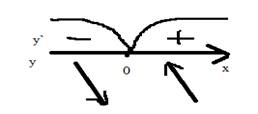
Рис. 3

Получаем, что  - экстремум функции.

2) вычислим значения функции в точке экстремума и на концах отрезка:

3) получаем, что ,    

б) 1)

        .

     y` = 0 ⟺  = 0

                        = 0

                        x(x-2) = 0

x=0 или x-2 = 0

x=0 или x=2 – стационарные точки.

Отметим стационарные точки на числовой прямой и определим знаки производной в каждом из получившихся промежутков (рис. 6)

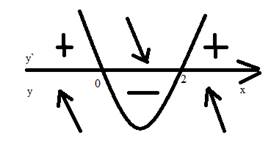
Рис. 6

Получаем, что  и  - экстремумы функции.

2) вычислим значения функции точках экстремума и на концах отрезка:

3) получаем, что , .

Задания для самостоятельной работы:

Контрольные вопросы (ответьте письменно):

1.    Запишите теоремы о связи знака первой производной с монотонностью функции.

2.    Запишите определение максимума (минимума) функции.

3.    Запишите определение экстремума функции.

4.    Запишите определение наибольшего (наименьшего) значений функции на промежутке.

5.