Практическая работа на тему:"Вычисление объемов"

Практическая работа №8

Тема: «Вычисление объемов»

Цель: уметь применять формулы для нахождения объемов тел вращения: цилиндра, конуса, усеченного конуса и шара при обосновании этапов решения задач; уметь выполнять чертежи любых тел вращения по условию задачи, понимать чертежи, находить на чертежах основные элементы тел вращения.

Оборудование: ручка, простой карандаш, линейка, методические рекомендации по выполнению работы.

Методические рекомендации по выполнению практической работы:

Задание №1. Прямоугольная трапеция с основаниями 6 см и 10 см и большей боковой стороной 5 см вращается вокруг меньшего основания. Найдите объем полученного тела вращения.

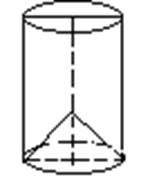
                                                                Рис. 1

Решение:

По условию задачи дана прямоугольная трапеция с основаниями 6 см и 10 см и большей боковой стороной 5 см, которая вращается вокруг меньшего основания (рис. 1). В результате получается цилиндр, внутри которого находится конус. Значит, чтобы найти объем полученного тела вращения, необходимо из объема цилиндра вычесть объем конуса.

Воспользуемся формулой .

Рассмотрим цилиндр, необходимо найти его радиус и высоту. Так как вращается прямоугольная трапеция вокруг своего меньшего основания, то высота цилиндра будет равна ее большему основанию, значит h=10 см, так как трапеция прямоугольная, то радиус цилиндра равен ее меньшей боковой стороне, то есть

Тогда объем цилиндра равен:

Найдем теперь объем конуса, высота которого равна: H=10-6=4 см, радиус конуса совпадает с радиусом цилиндра, то есть R=3 см, тогда объем конуса равен:

Теперь найдем объем полученного тела вращения:

Ответ: .

Задание №2. Из цилиндра, в осевом сечении которого лежит квадрат, вырезали шар, вписанный в этот цилиндр с площадью осевого сечения шара равной . Найдите объем полученного тела.

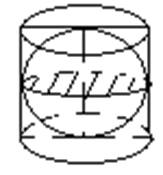
Рис. 2

Решение:

Объем полученного тела найдем по формуле: .

Рассмотрим осевое сечение шара, вырезанного из цилиндра. Осевое сечение шара есть круг, площадь которого вычисляется по формуле: , где  - радиус круга, так как шар вписан в цилиндр, то его радиус совпадает с радиусом основания цилиндра с одной стороны и с другой стороны радиус осевого сечения шара тоже равен радиусу основания цилиндра. Известно, что , причем , тогда

Таким образом, получили, что , так как в осевом сечении лежит квадрат, то  Найдем теперь объем тела вращения:

Ответ:

Задание №3. Цилиндр и конус имеют общие основание и высоту, причем образующая конуса равна 5 см. Найдите объем тела, полученного при удалении конуса из данного цилиндра, если площадь осевого сечения конуса равна 12 .

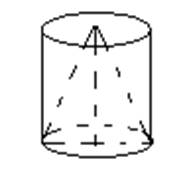
Рис. 3

Решение:

Объем полученного тела будем искать по формуле:

.

По условию известна также площадь осевого сечения конуса , причем в осевом сечений конуса лежит равнобедренный треугольник, площадь которого найдем по формуле: , таким образом, получаем, что .

С другой стороны, в прямоугольном треугольнике по теореме Пифагора имеем:

Применяя формулу , получим

Итак, имеем, что . Значит по формуле , имеем

,  .

Тогда искомый объем равен:

Ответ: .

Задания для самостоятельной работы:

Контрольные вопросы (ответьте письменно):

1.                  Запишите формулу для нахождения объема цилиндра.

2.                  Запишите формулу для нахождения объема конуса.

3.                  Запишите формулу для нахождения объема усеченного конуса.

4.                  Запишите формулу для нахождения объема шара.

5.