
Практическая работа
Тема. Решение нелинейных уравнений с помощью Ms Excel и MathCAD.
Цель работы. Изучение возможностей пакета Ms Excel при решении нелинейных уравнений. Приобретение навыков решения нелинейных уравнений в MathCAD.
Рекомендации к выполнению практической работы
Рассмотрим несколько примеров.
Пример 1. Найти корни полинома x3 - 0,01x2 - 0,7044x + 0,139104 = 0.
Для начала решим уравнение графически. Известно, что графическим решением уравнения f(x)=0 является точка пересечения графика функции f(x) с осью абсцисс, т.е. такое значение x, при котором функция обращается в ноль.
 Проведем
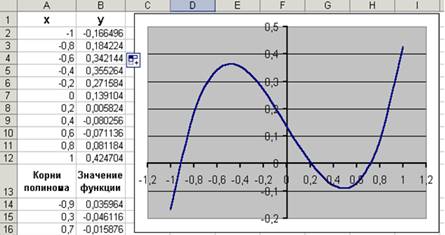
табулирование нашего полинома на интервале от -1 до 1 с шагом 0,2. Результаты
вычислений приведены на рис.1., где в ячейку В2 была введена формула: =
A2^3 - 0,01*A2^2 - 0,7044*A2 + 0,139104. На графике видно, что функция три
раза пересекает ось Оx, а так как полином третьей степени имеется не более трех
вещественных корней, то графическое решение поставленной задачи найдено. Иначе
говоря, была проведена локализация корней, т.е. определены интервалы, на
которых находятся корни данного полинома: [-1,-0.8], [0.2,0.4] и [0.6,0.8].
Проведем
табулирование нашего полинома на интервале от -1 до 1 с шагом 0,2. Результаты
вычислений приведены на рис.1., где в ячейку В2 была введена формула: =
A2^3 - 0,01*A2^2 - 0,7044*A2 + 0,139104. На графике видно, что функция три
раза пересекает ось Оx, а так как полином третьей степени имеется не более трех
вещественных корней, то графическое решение поставленной задачи найдено. Иначе
говоря, была проведена локализация корней, т.е. определены интервалы, на
которых находятся корни данного полинома: [-1,-0.8], [0.2,0.4] и [0.6,0.8].
Теперь можно найти корни полинома методом последовательных приближений с помощью команды Данные→Работа с данными→Анализ "что-если"→Подбор параметра... (см. рис. 2).
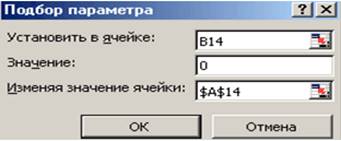 В поле Установить
в ячейке дается ссылка на ячейку, в которую введена формула, вычисляющая
значение левой части уравнения (уравнение должно быть записано так, чтобы его
правая часть не содержала переменную). В поле Значение вводим правую
часть уравнения, а в поле Изменяя значения ячейки дается ссылка на
ячейку, отведенную под переменную. Заметим, что вводить ссылки на ячейки в поля
диалогового окна Подбор параметров удобнее не с клавиатуры, а щелчком на
соответствующей ячейке.
В поле Установить
в ячейке дается ссылка на ячейку, в которую введена формула, вычисляющая
значение левой части уравнения (уравнение должно быть записано так, чтобы его
правая часть не содержала переменную). В поле Значение вводим правую
часть уравнения, а в поле Изменяя значения ячейки дается ссылка на
ячейку, отведенную под переменную. Заметим, что вводить ссылки на ячейки в поля
диалогового окна Подбор параметров удобнее не с клавиатуры, а щелчком на
соответствующей ячейке.
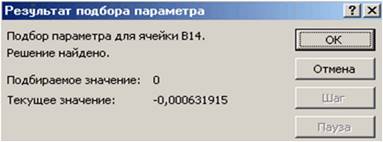 После
нажатия кнопки ОК появится диалоговое окно Результат подбора
параметра (см. рис. 3) с сообщением об успешном завершении поиска решения,
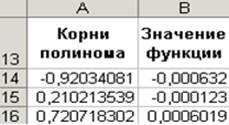
приближенное значение корня будет помещено в ячейку А14. Два оставшихся
корня находим аналогично. Результаты вычислений будут помещены в ячейки А15 и
А16 .
После
нажатия кнопки ОК появится диалоговое окно Результат подбора
параметра (см. рис. 3) с сообщением об успешном завершении поиска решения,
приближенное значение корня будет помещено в ячейку А14. Два оставшихся
корня находим аналогично. Результаты вычислений будут помещены в ячейки А15 и
А16 .
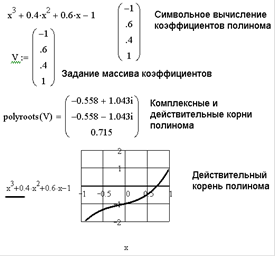
Пример 2. Найти решение уравнения x3 + 0,4x2 + 0,6x – 1,6 = 0.
Для решения задачи нужно задать массив коэффициентов v для дальнейшего использования в функции polyroots(v). Определить вектор коэффициентов многочлена можно при помощи символьной операции Symbolics → Polynomial Coefficient. При этом многочлен должен быть введен в рабочий лист, и одна из переменных выделена. Далее полученный вектор необходимо присвоить какой-либо переменной и найти решение, вызвав функцию вычисления корней полинома.
Задание 1. Найти корни полинома с помощью Ms Excel.
Задание 2. Найти корни полинома с помощью MathCAD.
|
№ варианта |
Уравнение |
№ варианта |
Уравнение |
|
1 |
|
5 |
|
|
2 |
|
6 |
|
|
3 |
|
7 |
|
|
4 |
|
8 |
|
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.