Практическая работа специальности 09.02.01.

Практическая работа №4 «Приведение формул к совершенным нормальным формам»

Цель работы: закрепить знание о ДНФ и КНФ, сформировать умение приводить формулы алгебры логики к СДНФ и СКНФ.

Ход работы

1. Познакомиться с теоретическим материалом.

2. Сделать краткий конспект теоретического материала в рабочих тетрадях (основные понятия, определения, формулы).

3. Подготовиться к опросу по контрольным вопросам.

4. Выполнить в тетрадях для практических работ или на ПК, используя программное обеспечение, указанное в работе, задания, соответствующие вашему варианту. (Номер варианта выбирается по последней цифре в порядковом номере в списке группового журнала. Если последняя цифра «0», то выбирается вариант 10)

5. Сдать выполненную практическую работу преподавателю.

Краткие теоретические сведения

Существуют две разновидности нормальных форм – дизъюнктивные (ДНФ) и конъюнктивные (КНФ).

Элементарной он н ей называется выражение, состоящее из конечного

числа переменных и их отрицаний, взятых в этом выражении не более одного раза и разделенных операциями дизъюнкции.

он н т ной нормальной формой (ДНФ) называется конъюнкция конечного

числа элементарных дизъюнкций.

Нормальная форма называется со ершенной, если в каждой ее элементарной дизъюнкции (конъюнкции) представлены все переменные, входящие в данную функцию (либо сами, либо с отрицанием).

Для того чтобы привести булеву функцию к совершенной нормальной форме, надо выполнить операции в следующем порядке.

– используя равносильности алгебры логики, заменить все имеющиеся операции на конъюнкцию, дизъюнкцию и отрицание;

– применяя законы де Моргана, снять отрицание с логических операций конъюнкции и дизъюнкции;

– используя распределительный и другие законы, привести функции к нормальной форме;

– используя законы идемпотентности, склеивания и др., минимизировать полученные булевы выражения;

– применяя правила операций с константами, привести минимизированные нормальные формы к совершенному виду.

Алгоритм получения СДНФ по таблице истинности:

1. Отметить те строки, в последнем столбце которых стоят 1:

2. Для каждой отмеченной строки выписать элементарные конъюнкции всех

переменных следующим образом: каждому аргументу будет соответствовать , а каждому будет соответствовать .

3. Объедините дизъюнкцией все полученные элементарные конъюнкции. Чтобы построить СКНФ по таблице истинности, надо взять дизъюнкцию

элементарных конъюнкций, дающих значение 0 и сделать ее отрицание. Примеры решения заданий

Пр мер 1. Постройте СДНФ и СКНФ по таблицы истинности для высказывания:

Решен е: Строим таблицу истинности - таблицу, с помощью которой устанавливается истинностное значение сложного высказывания при данных значениях входящих в него простых высказываний. Затем добавляем столбец и записываем в него элементарные конъюнкции.

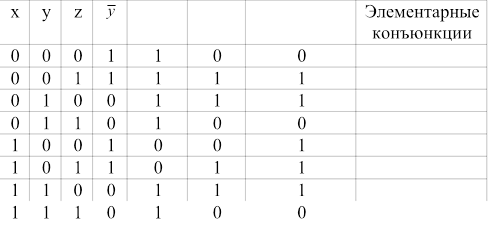Для получения СКНФ соединяем дизъюнкцией те элементарные конъюнкцией, в которых функция принимает значение 0, и делаем их отрицание:

Для получения СДНФ соединяем дизъюнкцией те элементарные конъюнкцией, в которых функция принимает значение 1:

Контрольные вопросы 1. Что такое ДНФ и КНФ?

2. Чем отличается ДНФ от СДНФ?

3. Как составить ДНФ по таблице истинности? 4. Как минимизировать ДНФ?

5. Как составить СКНФ по таблице истинности? 6. Как преобразовать ДНФ в СДНФ?

7. Как преобразовать КНФ в СКНФ?

Варианты заданий практической работы Вар ант 1