Поделиться
ПЗ 13 Решение задач по теме_Конечные автоматы.docx
1 Теория автоматов – раздел дискретной математики, изучающий математические модели реальных (технических, биологических, экономических) или возможных устройств, перерабатывающих дискретную информацию дискретными временными тактами
2 Автомат – это устройство, предназначенное для выполнения целенаправленных действий без участия человека, рассматриваемый либо как реализующий ту или иную формальную грамматику (абстрактный автомат), либо как множество элементов и схема их соединения (структурный автомат).
3 Автоматом Мили называется система A = (U, Q, V, δ ,λ), где множество
U={ u1 ,...,un } – входной алфавит, его элементы – входные сигналы, Q= { q1,...qm}
– множество внутренних состояний, множество V ={v1,...,vk } – выходной алфавит, его элементы – выходные сигналы, δ:U×Q→Q – функция переходов, λ :U×Q →V- функция выхода.
4 С конечным автоматом ассоциируется воображаемое устройство, которое может находиться в состоянии из множества Q, воспринимать сигналы из множества U и выдавать сигналы из множества V.
5 Схема называется комбинационной, если каждую из ее выходов можно представить, как булеву функцию входных переменных, типа И-НЕ, И, ИЛИ, ИЛИ-НЕ и т.д.
6 Графическое изображение комбинационной схемы, при котором показаны связи между различными элементами (вентелями), а сами элементы представлены условными обозначениями, называется функциональной схемой.
7 В ходе разработки комбинационных схем приходится решать задачи анализа и синтеза. Задача анализа комбинационной схемы состоит в определении статических и динамических свойств комбинационной схемы. Задача синтеза комбинационной схемы заключается в построении из заданного набора логических элементов комбинационной схемы, реализующей заданную систему булевых функций.
1 Для автоматов, заданных таблицами, построить диаграммы состояний.
2 Задать табличным способом автомат, заданный диаграммой состояний.
Исходные данные:
 |
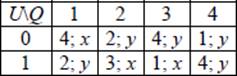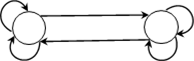
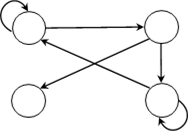
– Автомат имеет четыре состояния, его множество состояний Q = {1, 2, 3, 4}, следовательно, граф автомата будет с четырьмя вершинами.
– Входной алфавит U = {0, 1}, а выходной алфавит V = {x, y}
– В каждой ячейке два объекта, первый соответствует направлению дуги из текущей вершины графа
– Над дугой записываем пару значений: значение входного алфавита и выходной символ из ячейки
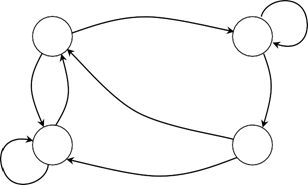Получим граф:
(1;у)
(0;у)
(0;х)
(1;у)
(0;у)
(1;х)
(0;у)
(1;х)
Задать табличным способом автомат, заданный диаграммой состояний
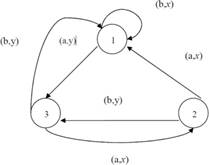
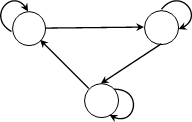
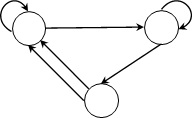
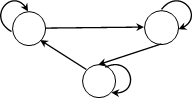
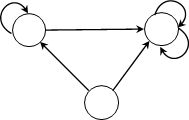
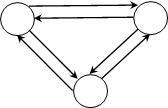
– Автомат имеет три состояния, его множество состояний Q = {1, 2, 3}, сле- довательно, в таблице четыре колонки.
– Над дугами пары объектов, первый – элемент входного алфавита, второй – выходного, значит входной алфавит U = {a, b}, а выходной алфавит V = {x, y}, в первой колонке две строки а и b
– В каждой ячейке два объекта, первый соответствует направлению дуги из текущей вершины графа, а второй – второму числу над соответствующей дугой
– Получим таблицу
|
U/Q |
1 |
2 |
3 |
|
a |
1, x |
1, x |
2, x |
|
b |
3, y |
3, y |
1, y |
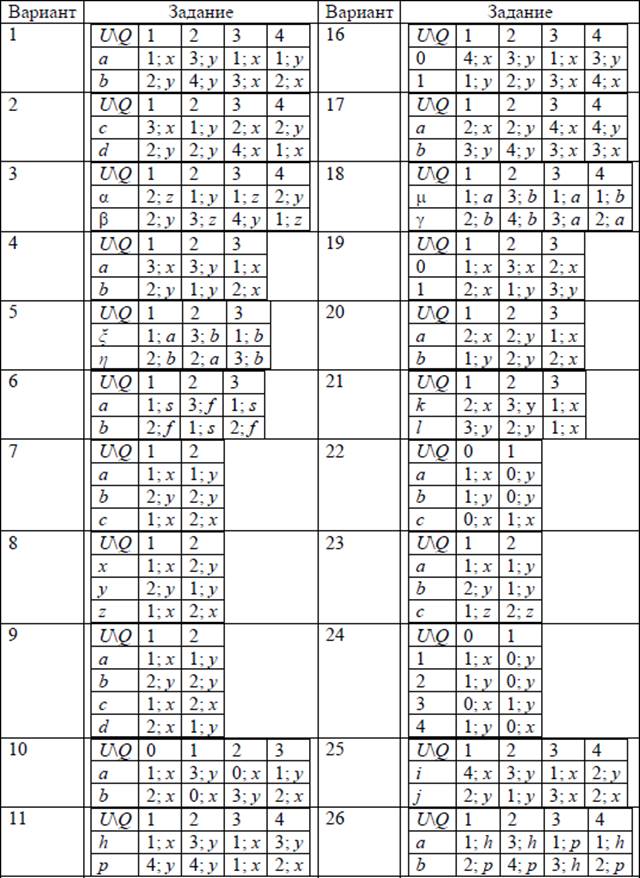Задания к практической работе.
Задание 1
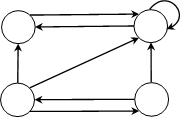
Задание
2
|
1 |
(а;х) (b;у) 1 2 (b;у) (a;у) (а;х) 4 3 (b;х) |
15 |
(x;х) (x;у) (y;у) 1 2 (y;у) (z;х) (z;х) |
|
2 |
(c;х) (a;x) (c;x) 0 (b;у) 1 (a;y) (b;y) |
16 |
(r;х) (s;у) (s;у) 1 2 (r;х) (r;у) (s;х) 3 |
|
3 |
(a;х) (b;у) (b;у) 1 (d;х) 2 (a;у) (c;х) (d;y) (c;х) |
17 |
(k;х) (l;у) (l;у) 1 2 (k;х) (k;у) 3 (l;х) |
|
4 |
(а;y) (a;x) 1 2 (b;у) (a;у) (b;у) 4 (а;х) 3 (a;y) (b;х) (b;х) |
18 |
(d;y) (d;y) 1 (c;у) 2 (d;x) (c;у) (c;x) 4 (d;х) 3 (b;х) |
|
5 |
(а;h) (b;p) 1 2 (b;p) (а;h) (a;h) 4 (b;p) (а;p) 3 (b;h) |
19 |
(a;x) 0 (b;x) 1 (b;x) (a;y) (a;y) (a;x) 3 (b;y) 2 (b;х) |
|
6 |
(f;y) (f;y) (r;x) 1 2 (f;х) (r;у) (r;x) 4 (f;х) 3 (r;y) |
20 |
(l;y) 1 (l;y) 2 (k;x) (k;y) (l;х) (k;у) (k;x) 4 3 (l;x) |
|
7 |
(μ;a) 1 (γ;b) 2 (γ;b) (μ;b) (μ;b) (μ;a) 4 (γ;a) 3 (γ;a) |
21 |
(α;z) (β;у) 1 2 (α;y) (β;z) (α;z) (β;z) (α;y) 4 (β;у) 3 |
|
8 |
(h;х)
1 (p;у) 2 (p;у) (p;х) (h;у) (p;х) (h;х) 4 (h;y) 3 (b;х) |
22 |
(r;x) 1 (s;y) 2 (s;y) (r;y) (r;x) (r;y) 4 (s;x) 3 (s;x) |
|
9 |
(a;x) (b;y) 1 2 (b;y) (a;y) (a;y) (a;x) 4 (b;x) 3 (b;x) |
23 |
(a;х) (b;у) (b;у) 1 (a;у) 2 (c;х) (c;х) |
|
10 |
(a;х) (b;у) (c;z) 1 (a;у) 2 (c;z) (b;y) |
24 |
(ξ;a) (η;a) (η;b) 1 2 (ξ;b) (ξ;b) 3 (η;b) |
|
11 |
(b;у) 1 (b;у) 2 (a;х) (a;у) (a;х) (b;х) 3 |
25 |
(k;x) (l;у) 1 2 (l;х) (k;х) (k;у) (l;y) 3 |
|
12 |
(b;y) (a;y) (a;x) 1 2 (a;x) (b;x) (b;y) 3 |
|
|
|
13 |
(1;у) (1;y) 1 2 (0;x) (0;у) (0;x) 4 3 (1;x) (0;y) (1;х) |
|
|
|
14 |
(j;y) 1 (j;y) 2 (i;x) (i;y) (i;y) (i;x) 4 (j;x) 3 (j;x) |
|
|
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.
