
Министерство образования, науки и молодежной политики Краснодарского края
Государственное бюджетное профессиональное образовательное учреждение
Краснодарского края
«Армавирский механико – технологический техникум»
Методическое пособие
для проведения
практического занятия
на тему:
«КРУЧЕНИЕ. ПОСТРОЕНИЕ ЭПЮР КРУТЯЩИХ МОМЕНТОВ. ОПРЕДЕЛЕНИЕ НАПРЯЖЕНИЙ В КОНСТРУКЦИОННЫХ ЭЛЕМЕНТАХ»
по дисциплине: «Техническая механика»
для студентов 2 курса
спец. 19.02.03, 19.02.06
Разработал преподаватель: Е.В. Игнатова
|
|
|
2018
1 ЦЕЛЬ РАБОТЫ
Знать:
- знать внутренние силовые факторы при кручении;
Уметь:
- определять напряжения в конструкционных элементах;
- строить эпюры крутящих моментов.
2 ДЛЯ ЗАЧЕТА РАБОТЫ НЕОБХОДИМО:
- изучить теоретический материал с помощью методического пособия;
- по варианту задания выполнить расчеты и построить эпюру крутящих моментов;
- ответить на контрольные вопросы.
3 КРАТКОЕ ИЗЛОЖЕНИЕ ТЕОРЕТИЧЕСКОГО МАТЕРИАЛА
3.1 Внутренние силовые факторы при кручении
Кручением называется нагружение, при котором в поперечном сечении бруса возникает только один внутренний силовой фактор — крутящий момент.
Внешними нагрузками также являются две противоположно натравленные пары сил.
Рассмотрим внутренние силовые факторы при кручении круглого бруса (чертеж 1).
Для этого рассечем брус плоскостью I и рассмотрим равновесие отсеченной части (чертеж 1а). Сечение рассматриваем со стороны отброшенной части.
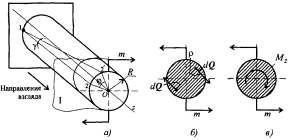
Чертеж 1
Внешний момент пары сил разворачивает участок бруса против часовой стрелки, внутренние силы упругости сопротивляются повороту. В каждой точке сечения возникает поперечная сила dQ (чертеж 1б). Каждая точка сечения имеет симметричную пару, где возникает поперечная сила, направленная в обратную сторону. Эти силы образуют пару с моментом dт = р dQ; р — расстояние от точки
до центра сечения. Сумма поперечных сил в сечении равна нулю:∑ dQ=0.
С помощью интегрирования получим суммарный момент сил упругости, называемый крутящим моментом:
Мк = ∫dт =∫ р dQ.
Практически крутящий момент определяется из условия равновесия отсеченной части бруса.
Крутящий момент в сечении равен сумме моментов внешних сил, действующих на отсеченную часть (чертеж 1в):
∑тz = 0, т. е. -т + Мz = 0; Мz=т=Мк.
3.2 Эпюры крутящих моментов
Крутящие моменты могут меняться вдоль оси бруса. После определения величин моментов по сечениям строят график-эпюру крутящих моментов вдоль оси бруса.
Крутящий момент считаем положительным, если моменты внешних пар сил направлены по часовой стрелке, в этом случае момент внутренних сил упругости направлен против часовой стрелки (чертеж 2).
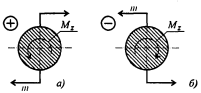
Чертеж 2
Порядок построения эпюры моментов аналогичен построению эпюр продольных сил. Ось эпюры параллельна оси бруса, значения моментов откладывают от оси вверх или вниз, масштаб построения выдерживать обязательно.
4 ПРИМЕР ВЫПОЛНЕНИЯ ЗАДАНИЯ
На распределительном валу (чертеж 3) установлены четыре шкива, на вал через шкив 1 подается мощность 12 кВт, которая через шкивы 2, 3, 4 передается потребителю; мощности распределяются следующим образом: Р2 = 8 кВт, Р3 = 3 кВт, Р4 = 1кВт, вал вращается с постоянной скоростью w = 25 рад/с. Построить эпюру крутящих моментов на валу.
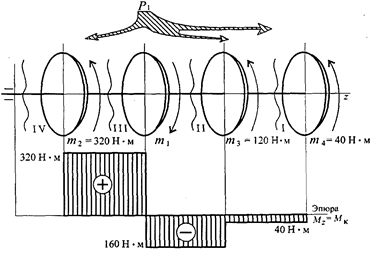
Чертеж 3
Решение:
1. Определить моменты пар сил на шкивах.
Вращающий
момент определяем из формулы мощности при вращательном движении Р = т
w, т = ![]() .
.
Момент на шкиве 1 движущий, а моменты на шкивах 2, 3, 4 — моменты сопротивления механизмов, поэтому они имеют противоположное направление. Брус скручивается между движущим моментом и моментами сопротивления. При равновесии момент движущий равен сумме моментов сопротивления:
т1 =![]() ;
;
т2 =![]() ;
;
т3 =![]() ;
;
т4 =![]() ;
;
т1 = т2 + т3 + т4
т1 = 320 + 120 + 40 = 480Нм.
2. Определить крутящие моменты в поперечных сечениях бруса, с помощью метода сечений.
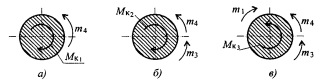
Чертеж 4
Сечение I (чертеж 4а):
- т4 + МК1 = 0; МК1 = т4; МК1 = 40 Нм — крутящий момент отрицательный.
Сечение II (чертеж 4б):
-т4 - т3 + МК2 = 0; МК2 =т4 + т3; МК2 = 40 +120 = 160 Нм — крутящий момент отрицательный.
Сечение III (чертеж 4в):
-т4 - т3 + т1 - МК3 = 0; -МК3 = т4 + т3 - т1 ; -МК3 = 40 + 120 - 480; МК3 = 320 Нм — крутящий момент положительный.
Сечение IV:
МК4 = -т4 - т3 + т1- т2 =0
3. Построить эпюру крутящих моментов. Известно, что скачок не эпюре всегда численно равен приложенному вращающему моменту.
Выбрать соответствующий масштаб.
Отложить значения моментов, заштриховать эпюру поперек, обвести по контуру, записать значения моментов (см. эпюру под схемой вала - чертеж 3). Максимальный крутящий момент на участке III, М К3 = 320Нм.
5 ЗАДАНИЕ
Для стального вала постоянного поперечного сечения:
1. Определить значения моментов М1, М2, М3, М4;
2. Построить эпюру крутящих моментов;
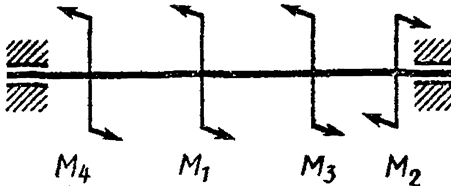
Рисунок 1
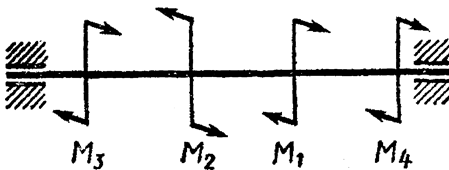
Рисунок 2
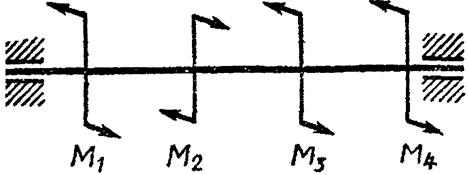
Рисунок 3
ВАРИАНТЫ ЗАДАНИЙ
|
Вариант |
Рисунок |
Р1, кВт |
Р3, кВт |
Р4, кВт |
w, рад/с |
|
1 |
3 |
1,5 |
1 |
3,5 |
16 |
|
2 |
2 |
5 |
1,5 |
2,5 |
18 |
|
3 |
1 |
7 |
6 |
4 |
25 |
|
4 |
3 |
1,2 |
8 |
5 |
35 |
|
5 |
2 |
1 |
3,2 |
6,3 |
25 |
|
6 |
1 |
8 |
5 |
3,2 |
25 |
|
7 |
3 |
3,5 |
2 |
1,5 |
20 |
|
8 |
2 |
1,1 |
6 |
3 |
35 |
|
9 |
1 |
7,5 |
8 |
2,5 |
40 |
|
10 |
3 |
2,5 |
4 |
1,5 |
20 |
|
11 |
2 |
5,5 |
7,3 |
1,8 |
32 |
|
12 |
1 |
1,4 |
1,1 |
6 |
45 |
|
13 |
3 |
4,5 |
5 |
3,5 |
23 |
|
14 |
2 |
1 |
1,8 |
5 |
20 |
|
15 |
1 |
8 |
6,5 |
4,5 |
30 |
|
16 |
3 |
4 |
1,2 |
2 |
20 |
|
17 |
2 |
9,5 |
4,5 |
4,4 |
18 |
|
18 |
1 |
4 |
3 |
3 |
16 |
|
19 |
2 |
6 |
2,5 |
2 |
25 |
|
20 |
3 |
9 |
3,2 |
4 |
20 |
|
21 |
2 |
5 |
4 |
3 |
18 |
|
22 |
1 |
6,5 |
3,5 |
2 |
25 |
|
23 |
3 |
3 |
1 |
2,5 |
30 |
|
24 |
2 |
5,5 |
5,5 |
3,5 |
35 |
|
25 |
1 |
1,1 |
2 |
6 |
15 |
|
26 |
3 |
1,5 |
1 |
5 |
45 |
|
27 |
2 |
2 |
1,5 |
5 |
10 |
|
28 |
1 |
8 |
2,6 |
4,5 |
40 |
|
29 |
3 |
2,4 |
4,1 |
3 |
14 |
|
30 |
2 |
4,6 |
5,2 |
4,2 |
20 |
6 КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Что такое кручение?
2. Когда крутящий момент считается положительной?
3. Какими линиями очерчены эпюры крутящих моментов?
4. Какие внутренние силовые факторы возникают при кручении?
5. Указать единицу измерения крутящего момента.
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.